Διαγράμματα στην Κβαντική Ηλεκτροδυναμική ή διαγράμματα Feynman

Άρθρο, Δεκέμβριος  2002

Ο Feynman μπροστά στον πίνακα δείχνοντας κάποια από τα φημισμένα διαγράμματά του. Είχαν λατρευτεί κυριολεκτικά από τους μαθητές του, για την απλοποίηση που πρόσφεραν στην δύσκολη θεωρία της Κβαντικής Ηλεκτροδυναμικής. Κάποτε ο Feynman είπε,  "Η θεωρία που έχω είναι πως ο καλύτερος τρόπος για να διδάξεις, είναι να μην φιλοσοφείς αλλά να είσαι χαοτικός".

ΕΙΣΑΓΩΓΗ

Για τους υπολογισμούς διαφόρων φαινομένων, στην Κβαντική Ηλεκτροδυναμική ή QED για συντομία, χρησιμοποιούνται τα λεγόμενα διαγράμματα Feynmann, τα οποία απλοποιούν πάρα πολύ όλη την υπολογιστική διαδικασία. Στην προσέγγιση που έκανε ο Feynmann με αυτά τα διαγράμματα, απεικονίζονται όλα τα στοιχειώδη σωματίδια που αλληλεπιδρούν, οι φορείς  των διαφόρων αλληλεπιδράσεων (φωτόνια, μποζόνια W, Z ή γκλουόνια) καθώς και τα παραγόμενα σωματίδια.

Όταν αλληλεπιδρούν δύο σωματίδια (ηλεκτρόνια, φωτόνια, ποζιτρόνια κλπ) δεν υπάρχει ένας μοναδικός τρόπος για το πως θα συμβεί. Η θεωρία μας λέει ότι υπάρχουν άπειροι τρόποι για να συμβεί.

Για παράδειγμα στην αλληλεπίδραση μεταξύ του φωτονίου και ενός ηλεκτρονίου δεν έχουμε μια θεωρία που να μας δίνει μια καθορισμένη αλληλουχία των εμπλεκομένων συμβάντων, μπορούμε όμως να υπολογίσουμε μόνο την πιθανότητα με την οποία μπορεί να συμβεί ένα ορισμένο φαινόμενο.

Η θεωρία QED προβλέπει ότι όσο πιο πολύπλοκη είναι μια διαδικασία τόσο μικρότερη είναι και η πιθανότητα πραγματοποίησής της. Σε κάθε επίπεδο πολυπλοκότητας, η συμμετοχή της αντίστοιχης διαδικασίας μειώνεται κατά ένα παράγοντα α=(1/137)² κι έτσι μετά από μερικά επίπεδα πολυπλοκότητας η συμμετοχή μιας διαδικασίας είναι αμελητέα. Ο παράγοντας α είναι η σταθερά λεπτής υφής, πολύ γνωστός στους φυσικούς από την ανάλυση των φασμάτων και αποτελεί μέτρο ισχύος της ηλεκτρομαγνητικής αλληλεπίδρασης.

Ένα άλλο παράδειγμα είναι η παρακάτω περίπτωση όπου το φως από την πηγή μπορεί να ανακλαστεί σε άπειρα σημεία πάνω στο κάτοπτρο για να φτάσει στον ανιχνευτή.

Στο σχήμα έχουμε μια πηγή φωτός S  και έναν ανιχνευτή Ρ. Τα φωτόνια από την πηγή μπορούν να ανακλαστούν από τον καθρέπτη και να φτάσουν στον ανιχνευτή Ρ. Άρα η διαδρομή ενός φωτονίου έχει πολλούς εναλλακτικούς δρόμους μέχρι να φτάσει στον ανιχνευτή Ρ. Η κβαντική λοιπόν θεώρηση του κόσμου μας λέει ότι το φως έχει ίσα πλάτη πιθανοτήτων (όλα τα βέλη  για τα οποία θα μιλήσουμε παρακάτω, έχουν ίσο μήκος) για να ανακλαστεί από τα διάφορα τμήματα του καθρέπτη από το Α έως Η.

Ο Feynman λοιπόν αμφισβήτησε τη βασική υπόθεση της κλασικής φυσικής ότι κάθε σωματίδιο έχει μια συγκεκριμένη ιστορία. Αντί αυτής, πρότεινε ότι τα σωματίδια κινούνται από ένα σημείο σε ένα άλλο ακολουθώντας κάθε δυνατή διαδρομή διαμέσου του χωροχρόνου.

Δεξιά: Η πάνω γραμμή είναι η κλασσική διαδρομή. Κάτω, στο ολοκλήρωμα διαδρομών του Feynman, το σωμάτιο ακολουθεί κάθε δυνατή διαδρομή.

Έτσι η Κβαντική Ηλεκτροδυναμική εγκατέλειψε τις προσπάθειες να υπολογίσει τις προβλέψεις για το πως ακριβώς θα συνέβαινε ένα γεγονός (πχ μια αλληλεπίδραση μεταξύ σωματιδίων) και περιορίστηκε στον υπολογισμό της πιθανότητας που είχε να συμβεί αυτό ανάμεσα σε πολλά πιθανά γεγονότα.

Οι κανόνες υπολογισμού της κβαντικής ηλεκτροδυναμικής

Οι κανόνες αυτής της σύνθεσης των πιθανοτήτων είναι οι παρακάτω:

1. Εάν ένα φαινόμενο μπορεί να επαληθευτεί με εναλλακτικούς τρόπους πρέπει να προσθέσουμε τις σχετικές πιθανότητες, οι οποίες οφείλονται σε κάθε διαφορετικό τρόπο.

2. Εάν ένα φαινόμενο συμβαίνει ως μια διαδοχή πολλών συμβάντων τότε οι σχετικές πιθανότητες, που οφείλονται σε κάθε συμβάν, πολλαπλασιάζονται.

Στην κβαντική ηλεκτροδυναμική αντιστοιχούμε στην πιθανότητα που υπάρχει να συμβεί ένα συμβάν πχ μια  απορρόφηση, ένα μικρό βέλος με τη βοήθεια μερικών κανόνων:

1ος κανόνας: Το τετράγωνο του μήκους του βέλους αντιστοιχεί στη πιθανότητα. Δηλαδή η πιθανότητα εκφράζεται ως το εμβαδόν ενός τετραγώνου με πλευρά το μήκος του βέλους. Για παράδειγμα αν η πιθανότητα να συμβεί ένα συμβάν είναι 4% τότε το βέλος έχει μήκος 0,2. 

Στην επιστημονική ορολογία το βέλος που παριστάνει την πιθανότητα να πραγματοποιηθεί ένα συμβάν, ονομάζεται πλάτος πιθανότητας.

2ος κανόνας: Αν ένα συμβάν μπορεί να πραγματοποιηθεί με πολλούς εναλλακτικούς τρόπους (όπως είδαμε πριν στην ανάκλαση των φωτονίων) , σχεδιάζουμε για κάθε τρόπο ένα βέλος και στο τέλος κάνουμε διανυσματικό άθροισμα των βελών, όπου το τελικό 'βέλος' έχει σαν αρχή την αρχή του πρώτου και σαν τέλος το τέλος του τελευταίου βέλους. Το τετράγωνο του τελικού βέλους μας δίνει την πιθανότητα να συμβεί ολόκληρο το συμβάν.

3ος κανόνας: Η διεύθυνση του κάθε βέλους προσδιορίζεται από κάποια γωνία στροφής ενός αρχικού βέλους. Η γωνία αυτή αντιστοιχεί στο χρόνο που χρειάζεται, ώστε ένα φωτόνιο να κινηθεί από την πηγή στον ανιχνευτή εκτελώντας την αντίστοιχη διαδρομή.

 Φυσικά υπάρχουν κι άλλοι κανόνες για τη σχεδίαση των βελών (πλατών πιθανότητας).

Διαγράμματα συμβάντων στο χωρόχρονο

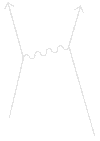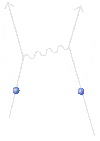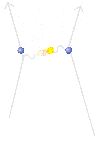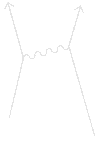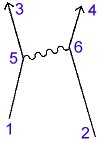Αυτά τα διαγράμματα είναι σχεδιαγράμματα για τον υπολογισμό πώς συμβαίνουν τα γεγονότα στη φύση - και δεν συμβαίνουν μόνο με έναν ακριβώς τρόπο: Παραδείγματος χάριν, δύο ηλεκτρόνια που πηγαίνουν από τη μια θέση του χωρόχρονου σε μια άλλη, μπορούν να το κάνουν με διάφορους τρόπους:

1. Ο ένας τρόπος είναι να ακολουθήσουν δύο ευθείες γραμμές, χωρίς να εκπέμψουν ή να απορροφήσουν κανένα φωτόνιο. Αυτό συμφωνεί κατά 99% στις πιθανότητες που υπάρχουν από το πείραμα και τους θεωρητικούς υπολογισμούς. Αλλά ο Feynman μπορούσε να το υπολογίσει με μεγαλύτερη ακρίβεια από αυτό.

2. Ένας άλλος τρόπος είναι να ακολουθήσουν τροχιές όπως εμφανίζεται στο ανωτέρω διάγραμμα. Δηλαδή ενδιάμεσα να εκπέμψουν ένα φωτόνιο, που δεν είναι πραγματικό, ώστε να ανιχνευτεί, αλλά virtual ή εικονικό όπως λέγεται, και μετά να συνεχίσουν την πορεία τους. Σημείωση: το φωτόνιο (ένα "εικονικό φωτόνιο") δεν ανιχνεύεται πραγματικά πηγαίνοντας από το ένα ηλεκτρόνιο σε άλλο. Το ηλεκτρόνιο που κινείται προς τα πίσω στο χρόνο θα μπορούσε να θεωρηθεί ως ποζιτρόνιο και δεν θα υπήρχε οποιαδήποτε διαφορά στα αποτελέσματα.
   
   Σημείωση 1: Το εικονικό φωτόνιο δεν ανιχνεύεται να πηγαίνει από το ένα ηλεκτρόνιο στο άλλο.
   Σημείωση 2: Ένα ηλεκτρόνιο που σχεδιάζεται να κινείται προς τα πίσω στο χρόνο θα μπορούσε να θεωρηθεί ποζιτρόνιο (αντισωμάτιο του ηλεκτρονίου), που κινείται με κανονική φορά στο χρόνο, χωρίς να υπάρχει οποιαδήποτε διαφορά στα αποτελέσματα.

3. Ένας άλλος τρόπος είναι, όπως στο διάγραμμα όπως εμφανίζεται ανωτέρω, αλλά με το εικονικό φωτόνιο να εξαφανίζεται προς ένα ζεύγος ποζιτρονίου - ηλεκτρονίου, το οποίο αμέσως μετά να εξαφανίζεται προς ένα νέο φωτόνιο, το οποίο να απορροφάται από το άλλο ηλεκτρόνιο. Πάλι, καμία από τις ενδιάμεσες δραστηριότητες δεν παρατηρείται πραγματικά, αλλά υπολογίζοντας αυτές τις πρόσθετες πιθανότητες, οι θεωρητικοί αριθμοί ταιριάζουν ακόμα περισσότερο με τις πιθανότητες που παρατηρούνται στο πείραμα.

4. Θα μπορούσαμε επίσης να έχουμε ένα διάγραμμα με δύο φωτόνια που εκπέμφθηκαν και που απορροφήθηκαν, ή ένα διάγραμμα στο οποίο ένα φωτόνιο να βγαίνει από το αριστερό ηλεκτρόνιο και να πηγαίνει απέναντι στο δεξιό ηλεκτρόνιο. Υπάρχουν πολλοί, πολλοί διαφορετικοί τρόποι που μπορεί να συμβεί η αλληλεπίδραση των ηλεκτρονίων, και τα διαγράμματα είναι μια συντομογραφία για να δείχνουν την πιθανότητα των συμβάντων.

Αλλά τι απεικονίζει αυτό το παραπάνω διάγραμμα;

Αυτό το διάγραμμα εμφανίζει την ηλεκτρομαγνητική αλληλεπίδραση δύο ηλεκτρονίων. Στην απλή αυτή περίπτωση, το φωτόνιο είναι φορέας της ηλεκτρομαγνητικής δύναμης ανάμεσα στα δύο ηλεκτρόνια και μεταφέρει ενέργεια και ορμή από το ένα ηλεκτρόνιο στο άλλο.

Στο διάγραμμα τα ηλεκτρόνια κινούνται από κάτω προς τα πάνω, (το πρώτο ξεκινάει από το σημείο 1 προς το 5, ενώ το δεύτερο από το 2 προς το 6). Στην θέση 5 ανταλλάσσουν ένα φωτόνιο, το οποίο είναι ένα φανταστικό, virtual, φωτόνιο, γιατί δεν μπορεί να συλληφθεί από κανένα όργανο, και το οποίο εκπέμπεται από το πρώτο και συλλαμβάνεται από το δεύτερο σχεδόν αμέσως. Μετά την ανταλλαγή του φωτονίου, οι κατευθύνσεις των ηλεκτρονίων αλλάζουν στο χωρόχρονο.

Τα φανταστικά αυτά φωτόνια δεν υπακούουν στο νόμο διατήρησης της ενέργειας, αλλά καλύπτονται από το νόμο της απροσδιοριστίας. Αφού το virtual φωτόνιο "δανείστηκε" ένα ποσό ενέργειας ΔΕ, ζει για ένα πολύ μικρό χρόνο Δt, που καθορίζεται από την αρχή της απροσδιοριστίας του Heisenberg ΔΕ.Δt=h/2π. Ακολούθως το φωτόνιο επιστρέφει την ποσότητα της ενέργειας που δανείστηκε και εξαφανίζεται.

Η αριστερή λοιπόν πάνω εικόνα είναι ένα διάγραμμα Feynman που απεικονίζει τις τρεις βασικές δράσεις που μπορούν να εμφανιστούν.

Κατά μήκος του Υ-άξονα (κατακόρυφος άξονας) είναι η κλίμακα του χρόνου. Όταν ένα σωματίδιο ταξιδεύει στον χρόνο και το χώρο η κυματιστή γραμμή έχει κλίση προς τα πάνω.

Αν η κυματιστή γραμμή είναι οριζόντια αυτό σημαίνει πως το σωματίδιο ταυτόχρονα (στον ίδιο χρόνο) εκπέμπεται και απορροφάται.

Ενώ αν η κυματιστή γραμμή είναι με φορά προς τα κάτω, θεωρείται πως ταξιδεύει προς το παρελθόν !

Ο Χ-άξονας (οριζόντιος άξονας) αντιπροσωπεύει το χώρο. Όλα τα σωματίδια (όπως τα ηλεκτρόνια και το φωτόνιο   που παριστάνονται εδώ), κινούνται μέσω του χρόνου και του χώρου.

Η κυματιστή γραμμή, σχηματίζει γωνία περίπου 45 μοιρών προς τα πάνω. Αυτό σημαίνει πως η απορρόφηση γίνεται αργότερα (μελλοντικά) από τον χρόνο εκπομπής του φωτονίου.

Ας σημειωθεί ότι ενώ τα σωματίδια πχ το ηλεκτρόνιο, έχουν κάποια φορά στην κίνηση τους, η κυματιστή γραμμή που δείχνει τη κίνηση του φωτονίου δεν έχει φορά. Αυτό συμβαίνει επειδή το φωτόνιο δεν αισθάνεται την κίνησή του. Έτσι στο ανωτέρω διάγραμμα το φωτόνιο μπορεί να κινείται και προς τις δύο κατευθύνσεις.

Τα ηλεκτρόνια  και οι αλληλεπιδράσεις τους με τα φωτόνια

Εδώ πρέπει να αναφέρουμε τα τρία στοιχειώδη γεγονότα της κβαντικής ηλεκτροδυναμικής, από τα οποία προκύπτουν όλα τα φαινόμενα που περιλαμβάνουν ηλεκτρόνια και φωτόνια:

1. Ένα φωτόνιο διαδίδεται από το σημείο 1 σε ένα άλλο σημείο 2 του χωροχρόνου.

2. Ένα ηλεκτρόνιο διαδίδεται από το σημείο 1 σε ένα άλλο σημείο 2 του χωροχρόνου.

3. Ένα ηλεκτρόνιο απορροφά ή εκπέμπει ένα φωτόνιο.

ΓΕΓΟΝΟΤΑ

1ο γεγονός: Ένα φωτόνιο διαδίδεται από μια θέση στην άλλη

Αυτό είναι το 1ο στοιχειώδες συμβάν που εξηγεί όλα τα φαινόμενα της Οπτικής: Ένα φωτόνιο κινείται από το σημείο 1 του χωροχρόνου στο σημείο 2.

Ένα φωτόνιο βρίσκεται αρχικά στο σημείο Α (Χ1, Τ1) του χωροχρόνου κι έχει ένα ορισμένο πλάτος πιθανότητας για να εμφανιστεί στο σημείο Β (Χ2, Τ2):  Το μέγεθος αυτού του πλάτους το ονομάζουμε Ρ(Α->Β). Όμως ένα τέτοιο πλάτος της πιθανότητας Ρ(Α->Β) εξαρτάται από τη διαφορά (X2-X1) και (T2-T1)   

Παρατηρούμε ότι η σχεδίαση του βέλους για το φωτόνιο είναι κυματιστό και έχει κλίση 45ο (διάδοση με τη ταχύτητα του φωτός).

2ο γεγονός: Ένα ηλεκτρόνιο κινείται από μια θέση στην άλλη

 Ένα ηλεκτρόνιο βρίσκεται αρχικά στο σημείο Α και μεταβαίνει στο Β κι έχει ένα ορισμένο πλάτος της πιθανότητας να εμφανιστεί στο σημείο 2, που το ονομάζουμε Ε (Α->Β). Το πλάτος εξαρτάται πάλι από τις διαφορές (X2-X1) και (T2-T1).

Το ηλεκτρόνιο το θεωρούμε απλό χωρίς πόλωση, ένα ηλεκτρόνιο χωρίς σπιν. Σύμφωνα με τον Pauli η κυματική ερμηνεία του του σπιν του ηλεκτρονίου είναι ένα πολωμένο κύμα.

3. Εκπομπή ή απορρόφηση ενός φωτονίου από ένα ηλεκτρόνιο.

Εδώ δεν ξεχωρίζουμε την εκπομπή ή την απορρόφηση και τις θεωρούμε σαν  ισοδύναμες διαδικασίες. Αυτό το συμβάν το  ονομάζουμε "σύζευξη". Το ηλεκτρόνιο που παριστάνεται με μια ευθεία γραμμή έχει ένα ορισμένο πλάτος για να εκπέμψει ή να απορροφήσει ένα φωτόνιο. Επειδή το πλάτος είναι το ίδιο είτε στην απορρόφηση είτε στην εκπομπή, χρησιμοποιούμε και για τις δύο περιπτώσεις τη λέξη "σύζευξη".

Το πλάτος για μια σύζευξη είναι ένας αριθμός που παριστάνεται από το γράμμα j. Για το ηλεκτρόνιο το πλάτος της σύζευξης j είναι -0.1 (αναφέρεται και ως "φορτίο").

Τα τρία στοιχειώδη συμβάντα για την αλληλεπίδραση ηλεκτρονίων

Οι συνδυασμοί μεταξύ της διάδοσης ηλεκτρονίων, της διάδοσης φωτονίων και της εκπομπής ή της απορρόφησης φωτονίων μας δίνει όλες τις περιπτώσεις.

Έστω ότι υπάρχουν δύο ηλεκτρόνια  και βρίσκονται στις θέσεις 1 και 2 του χωροχρόνου και καταλήγουν στις θέσεις 3 και 4. Αυτό μπορεί να γίνει με δύο τρόπους. Αυτές  οι δύο κινήσεις συνιστούν δύο υποσυμβάντα και τα βέλη τους πολλαπλασιάζονται για να δώσουν το τελικό βέλος.

Κάθε ένα στοιχειώδες συμβάν έχει ένα πλάτος -βέλος- που μπορούμε να το υπολογίσουμε με κάποιους κανόνες. Αυτά όμως τα συμβάντα συμβαίνουν στον τετραδιάστατο χωρόχρονο, όμως εδώ θα τα απεικονίζουμε σε δύο διαστάσεις, με μία μόνο χωρική διάσταση στον οριζόντιο άξονα και το χρόνο στον κατακόρυφο. 

ΤΡΟΠΟΣ Ι

 Αυτά τα συμβάντα, υπολογίζονται με τους τύπους Ε(1->3) και Ε(2->4) αντίστοιχα. Ο τύπος για το τελικό βέλος έχει τη μορφή (πολλαπλασιασμός των πλατών): Ε(1->3) * Ε(2->4)

ΤΡΟΠΟΣ ΙΙ

Κατόπιν υπολογίζουμε το πλάτος πιθανότητας του δεύτερου τρόπου για την κίνηση του ηλεκτρονίου από το 1->4 και από το 2->3 (διασταύρωση).  Ο τύπος για το τελικό πλάτος έχει τη μορφή: Ε(1->4) * Ε(2->3) (πάλι πολλαπλασιάζουμε τα πλάτη)

Οπότε αυτό το πλάτος της πιθανότητας από τον δεύτερο (ΙΙ) τρόπο, προστίθεται στο πλάτος του πρώτου Ι τρόπου.

Ας σημειώσουμε ότι: Οι τρόποι Ι και ΙΙ δεν περιέχουν όρους με j (σύζευξη) γιατί δεν έχουμε εκπομπή ή απορρόφηση φωτονίων.

Με εκπομπή και απορρόφηση φωτονίων

Δύο άλλοι τρόποι για την πραγματοποίηση αυτών των προηγούμενων συμβάντων είναι να εκπεμφθεί και ένα φωτόνιο από την θέση 5 και να απορροφηθεί στη θέση 6.

ΤΡΟΠΟΣ ΙΙΙ

Στην θέση 5 έχουμε εκπομπή φωτονίου (άρα πλάτος σύζευξης j). Επομένως πολλαπλασιάζουμε το πλάτος Ε στην θέση 5 με j. Ομοίως και στην θέση 6. Ανάμεσα στις θέσεις 5 και 6 έχουμε εκπομπή ή απορρόφηση φωτονίου με πλάτος Ρ. Τελικά θα έχουμε για το πλάτος για την πραγματοποίηση του συμβάντος με τον ανωτέρω τρόπο:

[Ε(1->5)*j*Ε(5->3)]*[Ε(2->6)*j*Ε(6->4)]*P(5->6)

ΤΡΟΠΟΣ IV

Το εύρος της πιθανότητας δίνεται από το προϊόν των ακόλουθων υπογεγονότων:

Ε (1->6)* j* Ε (4->6)* Ε (2->5)*j* Ε (5->3)*Ρ (5->6)

Συμπέρασμα: Για να πάνε δύο ηλεκτρόνια από τις θέσεις 1 και 2 στις θέσεις 3 και αντίστοιχα το συνολικό πλάτος της πιθανότητας δίνεται από το άθροισμα των πλατών των πιθανοτήτων, που συνδέονται με τους τρόπους που μελετήθηκαν πιο πάνω

 E(1->4)* E(2->3) + E(1->3)* E(2->4)+[Ε(1->5)*j*Ε(5->3)]*[Ε(2->6)*j*Ε(6->4)]*P(5->6)+

Ε (1->6)* j* Ε (4->6)* Ε (2->5)*j* Ε (5->3)*Ρ (5->6)

Συνοψίζοντας

Οι κόμβοι των ηλεκτρομαγνητικών αλληλεπιδράσεων ηλεκτρονίων ή ποζιτρονίων με φωτόνια

Στα παρακάτω σχήματα-διαγράμματα, για οικονομία στη σχεδίαση έχει απεικονιστεί ο χρόνος στον οριζόντιο άξονα και η χωρική διάσταση στον κατακόρυφο.

Κάθε κόμβος αναπαριστάνει μια ηλεκτρομαγνητική αλληλεπίδραση ή μπορεί να θεωρηθεί ένα σημείο καταστροφής ή γέννησης ενός σωματιδίου. Οι πιο πιθανοί κόμβοι είναι:

	Ένα ηλεκτρόνιο (ευθεία γραμμή) εκπέμπει ένα φωτόνιο (κυματιστή γραμμή) και σκεδάζεται ή μπορεί να θεωρηθεί ότι το ηλεκτρόνιο καταστρέφεται και μετά την εκπομπή του φωτονίου δημιουργείται ένα νέο ηλεκτρόνιο !
	Ένα ηλεκτρόνιο απορροφάει ένα φωτόνιο και σκεδάζεται
	Ένα ποζιτρόνιο (ένα ποζιτρόνιο είναι ηλεκτρόνιο με αντίθετη φορά στο χρόνο) εκπέμπει ένα φωτόνιο και σκεδάζεται.
	Ένα ποζιτρόνιο απορροφάει ένα φωτόνιο.
	Ένα φωτόνιο παράγει ένα ζεύγος ηλεκτρονίου-ποζιτρονίου.
	Ένα ηλεκτρόνιο συναντά ένα ποζιτρόνιο και εξαϋλώνονται, παράγοντας ένα φωτόνιο.

• Κάθε διάγραμμα που μπορεί να φτιαχτεί με τη βοήθεια των ανωτέρω τμημάτων είναι μια πιθανή διαδικασία που προβλέπει:

1. Διατήρηση της ενέργειας και ορμής σε κάθε κόμβο.

2. Οι γραμμές που εισέρχονται ή εξέρχονται από το διάγραμμα παριστάνουν πραγματικά σωματίδια που πρέπει να έχουν ενέργεια τέτοια που να ικανοποιούν τη σχέση E²=p²c²+m²c⁴.

3. Οι γραμμές στα ενδιάμεσα στάδια στο διάγραμμα παριστάνουν φανταστικά ή εικονικά "virtual" σωματίδια, που δεν χρειάζονται να έχουν τη σωστή σχέση μεταξύ E, p, και m, όμως τα οποία δεν μπορούν ποτέ να παρατηρηθούν.

Το πρώτο πράγμα που πρέπει να αναγνωρίσουμε είναι ότι κανένα απλό διάγραμμα δεν παριστάνει μια πιθανή διαδικασία.

Ακόμη και η πιο απλή διαδικασία, η σύγκρουση δύο σωματιδίων ή η σκέδαση, περιλαμβάνει πολλές πιθανά διαγράμματα.
Έστω η σύγκρουση ενός ηλεκτρονίου και ποζιτρονίου, που μας δίνει στο τέλος πάλι ένα ηλεκτρόνιο και ένα ποζιτρόνιο. Μόνο η ενέργεια και η ορμή τους αλλάζει σε αυτή τη διαδικασία.

Ο Feynman μας λέει ότι για αυτή τη σύγκρουση των δύο σωματιδίων πρέπει να σχεδιάσουμε όλα τα δυνατά, πιθανά, διαγράμματα. Αν βάλουμε κι ένα φωτόνιο να μεσολαβεί ανάμεσά τους, βρίσκουμε τρία διαγράμματα:

(α)	(β)	(γ)
Τα πρώτα δύο είναι το ίδιο γεγονός απλώς με διαφορετικό προσανατολισμό στο χρόνο. Το κάτω διάγραμμα δείχνει και τους δύο προσανατολισμούς.		Το τρίτο διάγραμμα είναι εντελώς διάφορη διαδικασία -- στο ενδιάμεσο στάδιο παρουσιάζεται μόνο ένα φανταστικό φωτόνιο.
Σημειώστε ότι δεν έχει προσανατολισμό ως προς το χρόνο, απλώς μια αρχή και ένα τέλος.

Μπορούμε όμως να σχεδιάσουμε και πιο πολύπλοκα διαγράμματα με περισσότερα φωτόνια.

ή

Και στην πράξη μπορεί να έχουμε οποιονδήποτε αριθμό φωτονίων

Τα τελευταία όμως διαγράμματα έχουν πολύ μικρή πιθανότητα να συμβούν καθόσον αρκετά πολύπλοκα.

Αυτό που κάνει τα διαγράμματα χρήσιμα είναι ότι κάθε διάγραμμα έχει ένα ορισμένο πολύπλοκο αριθμό ποσοτήτων  -- που ονομάζεται πλάτος -- που σχετίζεται με ένα σύνολο κανόνων (τους κανόνες Feynman).

Ένας κανόνας είναι ότι για κάθε φωτόνιο υπάρχει ένας πολλαπλασιαστικός παράγων j που ισούται με το τετράγωνο της σταθεράς λεπτοδομής a=1/137, για κάθε φωτόνιο. Έτσι τα πλάτη για τα διαγράμματα με πολλά φωτόνια γίνεται πολύ μικρό, αν συγκριθεί με διαγράμματα με έναν μόνο παράγοντα.

Ηλεκτρασθενείς αλληλεπιδράσεις και διαγράμματα Feynman 

Με παρόμοιο τρόπο γίνεται και η εκπομπή των μποζονίων W  στις ηλεκτρασθενείς αλληλεπιδράσεις.

Πρώτα ένα down κουάρκ που βρίσκεται στο νετρόνιο μετατρέπεται σε up. Το σωμάτιο W που ελευθερώνεται (σαν φορέας ασθενών αλληλεπιδράσεων) μπορεί να αλληλεπιδράσει με ένα νετρίνο και να προκύψει ένα βήτα σωματίδιο (αριστερή εικόνα) ή να διασπαστεί σε ένα αντινετρίνο και ένα ηλεκτρόνιο ή βήτα σωματίδιο (δεξιά εικόνα).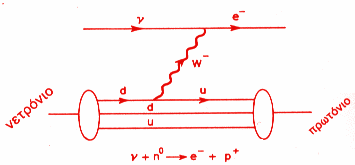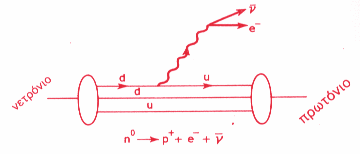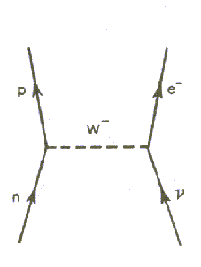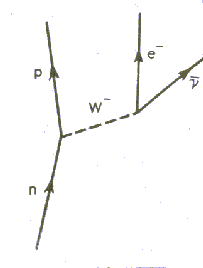

Στο ανωτέρω παράδειγμα (αριστερή εικόνα),  ένα νετρόνιο μαζί με ένα εισερχόμενο νετρίνο, μπορούν να μετατραπούν σε ένα πρωτόνιο, ένα ηλεκτρόνιο, ανταλλάσσοντας ένα μποζόνιο W^-- . Το μποζόνιο αυτό είναι ο φορέας της ηλεκτρασθενούς αλληλεπιδράσεως.

Αλλά η ίδια  αλληλεπίδραση, μπορεί να δοθεί διαφορετικά. Στην δεξιά εικόνα βλέπουμε ότι ένα νετρόνιο μετατρέπεται σε ένα πρωτόνιο, ανταλλάσσοντας ένα μποζόνιο W. Απλώς αντικαταστάθηκε το εισερχόμενο νετρίνο μ' ένα εξερχόμενο αντινετρίνο.

Με την ίδια λογική, στις αλληλεπιδράσεις ηλεκτρονίου και ποζιτρονίου, που είδαμε παραπάνω, ένα εισερχόμενο ηλεκτρόνιο μπορεί να αντικατασταθεί μ' ένα εξερχόμενο ποζιτρόνιο.

Το σωματίδιο W^-- ,προέκυψε από την αρχή της αβεβαιότητας. Το W "δανείστηκε" ενέργεια ΔΕ κι έτσι σχηματίσθηκε με βάση την αρχή ισοδυναμίας μάζας-ενέργεας. Μετά όμως από χρόνο Δt, που εμφανίζεται το  W^-- , απορροφάται εκ νέου. Ο χρόνος αυτός Δt είναι πολύ μικρός και δίνεται όπως είπαμε και πριν από την αρχή της απροσδιοριστίας του Heisenberg ΔΕ.Δt=h/2π.