Μια μαγική κατά βάθος θεωρία

H πρώτη διατύπωση της περίφημης Αρχής της Απροσδιοριστίας έκανε την εμφάνιση της το 1927, τότε που ο γερμανός φυσικός Werner Heisenberg απέδειξε ότι μπορείτε να μετρήσετε την ταχύτητα ενός ηλεκτρονίου ή τη θέση του, όχι όμως και τις δύο ταυτόχρονα με ακρίβεια. Συγκεκριμένα, ο Heisenberg απέδειξε ότι όσο καλύτερα μετράτε τη θέση ενός ηλεκτρονίου με τόσο μικρότερη ακρίβεια γνωρίζετε την ταχύτητα του, και αντιστρόφως. H μέτρηση είναι ένας συμβιβασμός και εσείς, ο πειραματικός, πρέπει να επιλέξετε τι θα μετρήσετε και να αποδεχθείτε τις συνέπειες.

Όπως και τόσα άλλα πράγματα στην κβαντική θεωρία, η αρχή της απροσδιοριστίας απορρέει από τον πιθανοκρατικό της χαρακτήρα. O Heisenberg στοχάστηκε πάνω σε μια διαδικασία όπου προσπαθούμε να μετρήσουμε τη θέση και την ταχύτητα ενός ηλεκτρονίου χρησιμοποιώντας ένα φωτόνιο που υφίσταται ανάκρουση από αυτό. Όταν, όμως, ένα φωτόνιο και ένα ηλεκτρόνιο συγκρούονται, δεν υπάρχει ένα μοναδικό προβλέψιμο αποτέλεσμα αλλά, αντίθετα, ένα ολόκληρο φάσμα δυνατών αποτελεσμάτων.

Η συναγωγή των ιδιοτήτων του ηλεκτρονίου από τη συμπεριφορά του ανακρούοντος φωτονίου δεν μπορεί παρά να μας οδηγήσει επίσης σε ένα φάσμα δυνατοτήτων, και όχι σε ένα μονοσήμαντο συμπέρασμα. Όθεν και η Αρχή της Απροσδιοριστίας.

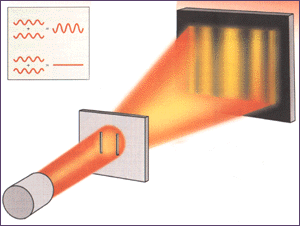Το πείραμα του Young

Με ελαφρώς διαφορετική μορφή, η αρχή αυτή έχει τις ρίζες της σε ένα παλιό πείραμα που πραγματοποίησε ο Thomas Young το 1801 για να αποδείξει ότι το φως είναι κύμα και όχι σωματίδιο. O Young άνοιξε δύο παράλληλες σχισμές, τη μία πλησίον της άλλης, σε ένα αδιαφανές πέτα-σμα, τις φώτισε, και στον τοίχο, πίσω από τις σχισμές, παρατήρησε φωτεινές και σκοτεινές ταινίες, ή κροσσούς — δηλαδή, μιαν εικόνα συμβολής. Ισχυρίστηκε, λοιπόν, πως αν το φως συνίστατο από σωματίδια που κινούνται ευθύγραμμα, αυτά θα έπρεπε να διέλθουν από τις σχισμές και να σχηματίσουν δύο φωτεινές κηλίδες. Επειδή όμως το φως είναι κύμα, τα όρη και οι κοιλάδες των δύο επιμέρους κυμάτων που εξέρχονται από τις σχισμές συμβάλλουν είτε ενισχυτικά είτε αποσβεστικά, δημιουργώντας αλλού φωτεινούς και αλλού σκοτεινούς κροσσούς.

Ας περάσουμε τώρα στα φωτόνια. Εφόσον είναι σωματίδια, θα έπρεπε να σχηματίζουν δύο φωτεινές κηλίδες. Μόνο που, σε αντίθεση με τις κλασικές σφαίρες, τα φωτόνια αλληλεπιδρούν όπως τα κύματα. Πρόκειται, δηλαδή, για σωματίδια με κυματικές ιδιότητες. Ή, αν προτιμάτε, είναι κύματα που συμπεριφέρονται ως ρεύμα σωματιδίων. Ακριβώς όπως ένα ημιεπαργυρωμένο κάτοπτρο σε ένα συμβολόμετρο «διαχωρίζει» τα φωτόνια, έτσι και η διάταξη των σχισμών του Young διαιρεί κάθε φωτόνιο σε δύο μέρη, τα οποία συμβάλλουν μεταξύ τους πίσω από το πέτασμα, δημιουργώντας την εικόνα συμβολής στον τοίχο. Αυτά τα «μέρη» των φωτονίων δεν είναι ανιχνεύσιμα: Εάν τοποθετήσετε ανιχνευτές ακριβώς πάνω στις σχισμές για να δείτε ποια πορεία ακολουθούν τα φωτόνια, θα καταστρέψετε την εικόνα συμβολής. Εάν αξιώσετε να δείτε τα φωτόνια να συμπεριφέρονται ως σωματίδια διερχόμενα από τη μία ή την άλλη σχισμή, καταστρέφετε την κυματική συμπεριφορά που δημιουργεί τους φωτεινούς και σκοτεινούς κροσσούς. Μπορείτε να παρατηρήσετε τα φωτόνια να συμπεριφέρονται ως κύματα ή να συμπεριφέρονται ως σωματίδια, όχι όμως και τα δύο ταυτόχρονα.

Αυτή η γενική ιδέα αποτελεί μία από τις χαρακτηριστικές ιδιότητες του κβαντικού κόσμου. Ανακαλέστε στη μνήμη σας το παράδοξο EPR και, ειδικότερα, το πώς ένα φωτόνιο επιδρά ακαριαία στον μακρινό του σύντροφο ως συνέπεια του πιθανοκρατικού χαρακτήρα των κβαντικών φαινομένων. Τα δύο πεπλεγμένα φωτόνια αποτελούν από κοινού φορείς της δυνατότητας πολλών πιθανών αποτελεσμάτων. Όσον αφορά το ποιο ακριβώς αποτέλεσμα θα παρατηρήσετε, αυτό παραμένει απροσδιόριστο έως ότου τα φωτόνια υποβληθούν σε πραγματική μέτρηση. Και εφόσον επιλέξετε να μετρήσετε μια συγκεκριμένη ιδιότητα, πρέπει να παραιτηθείτε από τη γνώση κάποιας άλλης.

Είναι παγκοίνως γνωστό ότι ο Αϊνστάιν αρνούνταν να αποδεχθεί την ιδέα ότι ο Θεός «παίζει ζάρια με το Σύμπαν…». Δεν τον ανησυχούσε απλώς ο πιθανοκρατικός χαρακτήρας της θεωρίας· τον θορυβούσαν κυρίως όλες οι ανατρεπτικές συνέπειες που απέρρεαν από αυτόν. Αρκετοί φυσικοί συμμερίστηκαν την πεποίθηση του Αϊνστάιν ότι η κβαντική θεωρία δεν μπορεί να είναι απολύτως ορθή. Έτσι, στην περίοδο που ακολούθησε συνέλαβαν και προέβαλαν μερικές ευφυείς ιδέες προκειμένου να διορθωθούν τα κακώς κείμενα.

Η πιθανοκρατική θεωρία του David Bohm

Το 1952, ένας αμερικανός φυσικός που είχε συνεργαστεί με τον Αϊνστάιν, ο David Bohm, πρότεινε μια εκδοχή της κβαντικής θεωρίας η οποία φαινόταν να διαλύει τις ανησυχίες του Αϊνστάιν.

Σύμφωνα λοιπόν με τη θεωρία του David Bohm, τα κβαντικά σωματίδια διαθέτουν «κρυμμένες μεταβλητές» (ή και λανθάνουσες παράμετροι), δηλαδή εσωτερικές ιδιότητες που είναι ιδιάζουσες και καθορισμένες για κάθε σωματίδιο.

Όταν εκτελείται μια μέτρηση, οι κρυμμένες μεταβλητές αλληλεπιδρούν με τη μετρητική συσκευή έτσι ώστε να παραχθεί ένα αποτέλεσμα. Μια συλλογή κβαντικών σωματιδίων, όσο προσεκτικά και αν προετοιμαστεί, χαρακτηρίζεται πάντοτε από ένα φάσμα τιμών των κρυμμένων μεταβλητών, ακριβώς όπως σε ένα σύνηθες, κλασικό αέριο μερικά άτομα κινούνται με ταχύτητα μεγαλύτερη από τη μέση και κάποια άλλα με μικρότερη.

Σ’ αυτή την εκδοχή της κβαντικής θεωρίας, οι μετρήσεις οδηγούν σε ένα φάσμα δυνατών αποτελεσμάτων, διότι οι εσωτερικές ιδιότητες των σωματιδίων που υποβάλλονται σε μέτρηση έχουν ένα φάσμα τιμών. Έτσι, η αρχή της απροσδιοριστίας επιζεί. Από πρακτική άποψη, η θεωρία του Bohm είναι ακριβώς ισοδύναμη με τη συμβατική κβαντική θεωρία. Αποτελεί, ουσιαστικά, μια μαθηματική αναδιατύπωση και επανερμηνεία των καθιερωμένων εξισώσεων και, συνεπώς, οδηγεί στα ίδια αποτελέσματα.

Υπάρχει όμως ένα αγκάθι: η κβαντική θεωρία έχει κάποια ιδιάζοντα μη κλασικά χαρακτηριστικά, οπότε, μολονότι ο Bohm προσπάθησε να αποκαταστήσει την κλασική προσδιοριστικότητα των κβαντικών σωματιδίων, η θεωρία του δεν μπορεί να είναι πραγματικά κλασική. Και δεν είναι.

Στο πείραμα των δύο σχισμών, για παράδειγμα, η θεωρία του Bohm υποστηρίζει ότι ένα φωτόνιο διέρχεται οπωσδήποτε ή από τη μία ή από την άλλη σχισμή. Αλλά τότε, πώς παράγεται η εικόνα συμβολής στον τοίχο; H απάντηση κρύβεται σε μια οντότητα που ονομάζεται «κύμα-πιλότος». O Bohm ισχυρίζεται ότι υπάρχουν ταυτοχρόνως και κύματα και σωματίδια, και μάλιστα, ότι είναι εντελώς διακεκριμένα. To κύμα-πιλότος διέρχεται από τις δύο σχισμές ακριβώς όπως ένα κλασικό κύμα και δημιουργεί την εικόνα συμβολής. To σωματίδιο ακολουθεί το κύμα-πιλότο, γεγονός το οποίο δικαιολογεί άλλωστε και το όνομα του. Τα φωτόνια που διέρχονται μέσα από τις σχισμές, με τη μορφή ενός ρεύματος, έχουν ελαφρώς διαφορετικές ενέργειες και κατευθύνσεις· έτσι, ακολουθούν το κύμα-πιλότο ακριβώς όπως οι βόλοι κυλάνε σε ένα κομμάτι κυματοειδές χαρτόνι, διανύοντας διαφορετικές διαδρομές ανάλογα με την αρχική κατάσταση από την οποία εκκινούν. Τα φωτόνια φθάνουν στον τοίχο καθοδηγούμενα από το κύμα-πιλότο και σχηματίζουν την αναμενόμενη εικόνα συμβολής.

Πρόκειται για ενδιαφέρουσα άποψη. H μεγάλη δυσκολία, όμως, έγκειται στο να εξηγήσουμε τι ακριβώς είναι αυτό το κύμα και πώς καθοδηγεί τα φωτόνια. Πάντως, αποκλείεται να είναι ένα κλασικό κύμα που καθοδηγεί τα φωτόνια ασκώντας τους κάποια δύναμη, διότι τότε οι ενέργειες των φωτονίων θα μεταβάλλονταν —πράγμα το οποίο δεν συμβαίνει.

H μυστηριώδης φύση του κύματος-πιλότου εκδηλώνεται σαφέστερα σε ένα πείραμα EPR. Εδώ, το κύμα-πιλότος μεταβιβάζει διαπιστωμένα πληροφορία από το ένα διαπλεγμένο σωματίδιο στο άλλο, έτσι ώστε οι μετρήσεις που πραγματοποιούνται στο ζεύγος να δίνουν πάντοτε τα αναμενόμενα αποτελέσματα. H εν λόγω μεταβίβαση, όμως, πρέπει να συντελείται ακαριαία. Φαίνεται, λοιπόν, ότι το κύμα-πιλότος συνιστά τη φυσική ενσάρκωση της παλαιάς έννοιας της «δράσης εξ αποστάσεως». Πρόκειται, δηλαδή, για ό,τι ακριβώς πάσχιζε να αποφύγει πάση θυσία ο Αϊνστάιν.

Οι πολλοί κόσμοι του Hugh Everett

hugh-everett Μια πενταετία αφότου ο Bohm διατύπωσε τη δική του εκδοχή της κβαντικής θεωρίας με κρυμμένες μεταβλητές, ο Hugh Everett το 1957, τελειόφοιτος τότε φυσικός του Πανεπιστημίου του Πρίνστον, είχε μια τελείως διαφορετική έμπνευση. Σε ένα πείραμα EPR, για παράδειγμα, μπορεί να γνωρίζουμε ότι το ένα φωτόνιο του ζεύγους είναι κατακόρυφα πολωμένο, οπότε το άλλο πρέπει να είναι οριζόντια πολωμένο. Εύκολα, όμως, θα μπορούσε να συμβαίνει και το αντίστροφο. Ανακύπτει, λοιπόν, το εύλογο ερώτημα γιατί πραγματοποιείται το ένα ενδεχόμενο ενώ το άλλο όχι.

O Everett ισχυρίστηκε ότι πραγματοποιούνται και τα δύο ενδεχόμενα — σε διαφορετικά, όμως, σύμπαντα. Υποστήριξε ότι, οποτεδήποτε εκτελείται μια κβαντική μέτρηση, συντελείται ένας «διαχωρισμός» σε διαφορετικά σύμπαντα — ένα για κάθε πιθανό αποτέλεσμα. Εμείς παρατηρούμε ένα συγκεκριμένο αποτέλεσμα επειδή βρισκόμαστε στο σύμπαν όπου πραγματώνεται αυτό και όχι κάποιο άλλο. Στα άλλα σύμπαντα, τα «αντίγραφα» μας γίνονται μάρτυρες κάποιου από τα υπόλοιπα δυνατά αποτελέσματα. H διαδικασία αυτή επαναλαμβάνεται επ’ άπειρον, και η σειρά των αλλεπάλληλων «διαχωρισμών» σε παράλληλα σύμπαντα μακραίνει και πλουτίζεται με ολοένα και νέες «διακλαδώσεις».

H θεωρία των πολλών κόσμων του Everett αφήνει την κβαντική θεωρία εντελώς άθικτη σε ό,τι αφορά το τεχνικό περιεχόμενο της. Πρόκειται, αν θέλετε, για μια μεταφυσική ερμηνεία της ίδιας παλιάς θεωρίας. Ακόμη και το ερώτημα αν αυτά τα άλλα σύμπαντα είναι πραγματικά παραμένει αδιευκρίνιστο. To να ρίξετε μία φευγαλέα ματιά σε ένα σύμπαν διαφορετικό από το δικό σας ισοδυναμεί με παραβίαση της αρχής της απροσδιοριστίας. Θα σήμαινε, για παράδειγμα, ότι μπορείτε να μετρήσετε την ταχύτητα ενός ηλεκτρονίου σε ένα σύμπαν, τη θέση του σε ένα άλλο, και έπειτα να συνδυάσετε τα αποτελέσματα και απ’ τα δύο σύμπαντα για να κατανικήσετε τον περιορισμό που όρθωσε ο Heisenberg.

Συνεπώς, αφ’ ης στιγμής τα γέννησε κάποια μέτρηση, αυτά τα διαχωρισμένα σύμπαντα οφείλουν να παραμείνουν αυστηρώς και απολύτως διαχωρισμένα. Είναι, άραγε, πραγματικά ή όχι; H απόφαση επαφίεται σ’ εσάς. Oi διαμάχες που περιστρέφονται γύρω από τις «ερμηνείες» της κβαντικής θεωρίας έχουν ήδη διαρκέσει πάρα πολύ και σε τελική ανάλυση, κατά τη γνώμη ορισμένων, στερούνται νοήματος —δεδομένου ότι, λόγω των προϋποθέσεων τους και της λογικής που τις διέπει, οδηγούν κατ’ ανάγκην στα ίδια πρακτικά αποτελέσματα. Στην πραγματικότητα, το όλο ζήτημα ανάγεται στο ποια νοητική εικόνα του κβαντικού κόσμου βρίσκετε ελκυστικότερη.

Το θεώρημα Bell

john_bell Κατέστη δυνατόν, ωστόσο, να αποδείξουμε ότι η κβαντική θεωρία διαφέρει θεμελιωδώς από την κλασική φυσική. Το 1964 ο φυσικός John BeIl διατύπωσε ένα απλό και κομψό θεώρημα, που φέρει πλέον το όνομα του. Αφορά ένα πείραμα EPR όπου δύο διαπλεγμένα σωματίδια εκτοξεύονται σε διαφορετικές διευθύνσεις, κατά τα συνήθη. O BeIl μελέτησε τι θα συνέβαινε εάν δύο πειραματικοί δεν ήταν υποχρεωμένοι να μετρούν, για παράδειγμα, την πόλωση ενός φωτονίου σε μια προκαθορισμένη διεύθυνση, αλλά μπορούσαν να επιλέξουν τυχαία ανάμεσα σε μετρήσεις της πόλωσης σε διαφορετικές γωνίες.

Από την άποψη της κλασικής φυσικής, αφ’ ης στιγμής δύο σωματίδια EPR απομακρυνθούν ακολουθώντας το καθένα τη δική πορεία, αδυνατούν να επηρεάσουν το ένα το άλλο. Σύμφωνα με την κβαντική θεωρία, ωστόσο, η υπερφυσική σύνδεση διατηρείται — αν και δύσκολα μπορούμε να προσδιορίσουμε σε τι ακριβώς συνίσταται αυτή η σύνδεση ή να βρούμε έναν τρόπο για να την ποσοτικοποιήσουμε. Ακριβώς αυτό επιτυγχάνει το θεώρημα του BeIl: λέει ότι σε μια σειρά μετρήσεων διαδοχικών ζευγών σωματιδίων EPR ανακύπτουν στατιστικές διαφορές ανάμεσα στην κβαντική και την κλασική εικόνα. Τα κβαντικά σωματίδια παρουσιάζουν πολύ υψηλότερο βαθμό συσχέτισης απ’ ό,τι τα κλασικά, πράγμα το οποίο μπορούμε να αποδείξουμε υποβάλλοντας σε απλούς μαθηματικούς ελέγχους τα αποτελέσματα που προκύπτουν από μια σειρά μετρήσεων ζευγών EPR.

O BeIl εισήγαγε μια μαθηματική ποσότητα για την οποία η κβαντική θεωρία προβλέπει τιμές μεγαλύτερες από εκείνες που είναι δυνατόν να προκύψουν βάσει οποιασδήποτε κλασικής εικόνας. Χρειάστηκε να περάσει μια εικοσαετία ώσπου να ελεγχθεί επιτυχώς το θεώρημα του BeIl. Και τούτο επειδή η πραγματοποίηση των αναγκαίων πειραμάτων με την απαιτούμενη αξιοπιστία και ακρίβεια παρουσίαζε σημαντικές δυσχέρειες.

To 1982, όμως, οι προσπάθειες του Alain Aspect και της ομάδας του στο Πανεπιστήμιο του Παρισιού στέφθηκαν επιτέλους με επιτυχία. Τα πειραματικά αποτελέσματα δικαίωσαν την κβαντική θεωρία, γεγονός που, αν μη τι άλλο, έσβησε και την παραμικρή εναπομένουσα ελπίδα για μια μελλοντική παλινόρθωση της κλασικής φυσικής. Ακριβέστερα, ο έλεγχος του θεωρήματος του BeIl από τον Aspect έδειξε ότι κάθε προσπάθεια αναδιατύπωσης της κβαντικής μηχανικής υπό τη μορφή μιας ψευδοκλασικής θεωρίας είναι καταδικασμένη σε αποτυχία. H κβαντική θεωρία είναι και θα παραμείνει πάντα πραγματικά διαφορετική.

H φύση της διαφοράς έγκειται, βασικά, σε μια έννοια που λέγεται «μη τοπικότητα». H κλασική φυσική ενσωματώνει έναν αυστηρά τοπικό νόμο αιτίας-αποτελέσματος. Ό,τι συμβαίνει σε ένα σημείο A μπορεί να προκαλέσει αμέσως κάποιο αποτέλεσμα μόνο στο σημείο A, ενώ, αν το αποτέλεσμα εκδηλωθεί στο σημείο B, κάποια φυσική επίδραση πρέπει να έχει διαδοθεί από το A στο B, γεγονός που απαιτεί χρόνο για να πραγματοποιηθεί.

H κβαντική θεωρία είναι μη τοπική. Στα πειράματα EPR, μια μέτρηση σε ένα σημείο A έχει μια ασύλληπτη, ακαριαία και — σύμφωνα με το θεώρημα του BeIl — ποσοτικόποιήσιμη επίδραση στο σημείο B. Av και κατά πόσον ταξιδεύει κάτι το φυσικό από το A στο B, αυτό είναι αντιλεγόμενο. Στη θεωρία του Bohm, την ακαριαία επίδραση τη μεταφέρει το κύμα-πιλότος. Στο πλαίσιο της θεωρίας των πολλών κόσμων του Everett, η μη τοπικότητα διαχέεται σε καθένα από τα πολλά σύμπαντα. Πάντως, όπως και να το δείτε, η παρουσία της μη τοπικότητας στον κβαντικό κόσμο αποτελεί γεγονός.

Οι μετρήσεις στην ερμηνεία της κβαντικής θεωρίας

Στον πραγματικό κόσμο δεν συναντάμε γάτες που να είναι ταυτοχρόνως ζωντανές και
νεκρές. Τι τις αναγκάζει, λοιπόν, να επιλέξουν τη ζωή ή το Θάνατο;

Στον κβαντικό κόσμο, οι μετρήσεις είναι εκείνες που «κάνουν τα πράγματα να συμβαίνουν». Όποτε πραγματοποιείται μια μέτρηση, μέσα από ένα πλήθος δυνατοτήτων αναδύεται μια καθορισμένη απάντηση. Χωρίς μετρήσεις, επομένως, ολόκληρο το Σύμπαν θα έλιωνε σε μια ομίχλη απροσδιοριστίας χωρίς αρχή και τέλος. Αλλά τι είναι, τέλος πάντων, η μέτρηση; Προϋποθέτει, άραγε, την ανθρώπινη παρέμβαση ή παρατήρηση, ή μήπως οι μετρήσεις μπορεί να συντελούνται εν αγνοία των ανθρώπων (όπως όταν πέφτει ένα δέντρο μέσα στο δάσος χωρίς να το κοιτάζει κανείς); Και, αν υποθέσουμε ότι ξέρουμε τι εστί μέτρηση, πώς ακριβώς αναγκάζει ένα κβαντικό σύστημα να επιλέξει ανάμεσα στα διάφορα ενδεχόμενα και να αποφασίσει σε ποια συγκεκριμένη κατάσταση πρέπει να μεταβεί;

Όταν ο Niels Bohr συνέθετε την αντίληψη της κβαντικής θεωρίας που έγινε γνωστή ως ερμηνεία της Κοπεγχάγης, είχε βαθιά επίγνωση της σημασίας των εν λόγω ερωτημάτων. Αδυνατούσε, όμως, να βρει ικανοποιητικές απαντήσεις, και την αδυναμία του αυτή δεν την έκρυψε. Οι μετρήσεις είναι δυνατές, είπε· το ξέρουμε εκ πείρας. Σε τελική ανάλυση, οι ανιχνευτές φωτονίων καταγράφουν τα φωτόνια. Υιοθετώντας μια πραγματιστική στάση, ο Bohr υποστήριξε ότι η μέτρηση είναι η διαδικασία εκείνη που υποχρεώνει το κβαντικό σύστημα να βρεθεί σε μια καθορισμένη κατάσταση. Ομολογουμένως, πρόκειται για έναν μάλλον κυκλικό ορισμό· αν όμως τον αποδεχθείτε, όλα τα υπόλοιπα έπονται. H αρχή αυτή, το ουσιαστικό νόημα της οποίας συμπυκνώνεται στο ότι μας αποτρέπει από περαιτέρω προβληματισμούς για το τι είναι μέτρηση, αποτελεί τον θεμέλιο λίθο της ερμηνείας της Κοπεγχάγης.

Αναζητείται νεκρή ή ζωντανή

Ωστόσο, είναι ενοχλητικό να έχεις μια θεμελιώδη φυσική θεωρία η οποία, όσο και αν η αποτελεσματικότητα της δεν αμφισβητείται, στηρίζεται σε μια αρχή που ουδείς διανοήθηκε ποτέ να ισχυριστεί ότι την κατανοεί. Ιδιαίτερα δυσαρεστημένη με αυτή την κατάσταση των πραγμάτων ήταν η γάτα του Erwin Schrodinger. H δυστυχής γάτα βρίσκεται κλεισμένη σε ένα κιβώτιο, μόνη μαζί με έναν μηχανισμό ο οποίος εκπέμπει ένα φωτόνιο προς ένα φίλτρο και καταγράφει αν το φωτόνιο θα διέλθει μέσα από αυτό ή όχι.

Εάν δεν διέλθει, δεν συμβαίνει απολύτως τίποτε. Εάν διέλθει, όμως, το φωτόνιο ενεργοποιεί μια διάταξη η οποία σπάει ένα φιαλίδιο με δηλητηριώδες αέριο, προκαλώντας έτσι το θάνατο της άτυχης γάτας. To πείραμα σχεδιάζεται ώστε η πιθανότητα να διέλθει το φωτόνιο από το φίλτρο είναι 50%. Συνεπώς, εάν ανοίξετε το κιβώτιο και κοιτάξετε μέσα, υπάρχει 50% πιθανότητα η γάτα να πηδήξει έξω ζωντανή.

Ως εδώ, όλα καλά.

H δυσκολία παρουσιάζεται, όπως έδειξε ο Schrodinger το 1935, όταν αρχίσουμε να αναρωτιόμαστε τι συνέβη μέσα στο κιβώτιο μετά τη μέτρηση του φωτονίου αλλά προτού σηκώσει κανείς το σκέπασμα. Μια αρκετά απλή εικασία είναι να πούμε ότι ο μηχανισμός εξέπεμψε το φωτόνιο, το φωτόνιο ή διήλθε μέσα από το φίλτρο ή όχι, το φιαλίδιο με το δηλητήριο ή έσπασε ή παρέμεινε ανέπαφο, οπότε και η γάτα ή πέθανε ή διατηρείται εν ζωή.

Αν έτσι έχουν τα πράγματα, άπαξ και το φωτόνιο προσέπεσε στο φίλτρο, πραγματοποιήθηκε μια κβαντική μέτρηση, και τα γεγονότα που ακολούθησαν εξασφάλισαν ότι από τη στιγμή εκείνη και στο εξής το κουτί περιείχε ή μια ζωντανή ή μια νεκρή γάτα. Αυτό, όμως, σημαίνει ότι θεωρούμε πως δεν χρειαζόταν τίποτε περισσότερο από την πρόσπτωση του φωτονίου στο φίλτρο για να έχουμε μια μέτρηση. Από την άλλη, όμως, τι θα λέγαμε αν απαιτούνταν η ανθρώπινη παρατήρηση για να δρομολογηθεί η μέτρηση; Στην προκειμένη περίπτωση, ώσπου να ανοίξει κάποιος το κιβώτιο και να κοιτάξει μέσα, η γάτα θα έπρεπε να βρίσκεται σε κάποια απροσδιόριστη κβαντική κατάσταση, όντας ούτε ζωντανή ούτε νεκρή αλλά εν δυνάμει και τα δύο. Ti μπορεί όμως να σημαίνει — αν μπορεί να σημαίνει κάτι — το να λέμε ότι μια γάτα βρίσκεται σε μια απροσδιόριστη κατάσταση όπου είναι μισό νεκρή και μισοζωντανή;

O Bohr απάντησε χωρίς περιστροφές: δεν έχει σημασία. Το μοναδικό πράγμα που μπορούμε να ελέγξουμε είναι ότι, όταν ανοιχτεί το κουτί, θα βρούμε την έγκλειστη γάτα ή νεκρή ή ζωντανή. Ουδείς λόγος συντρέχει να ανησυχούμε για το τι μπορεί να σημαίνει μια μισονεκρή – μισοζωντανή γάτα. Και τούτο επειδή κανείς δεν πρόκειται να παρατηρήσει ποτέ κάτι τέτοιο. Κάθε γάτα που θα δείτε θα είναι πάντοτε ή νεκρή ή ζωντανή.

Ωστόσο, εδώ ανακύπτει ένα πραγματικό πρόβλημα φυσικής. H θέση του Bohr συνεπάγεται ότι υπάρχουν κβαντικά αντικείμενα, όπως τα φωτόνια, που είναι δυνατόν να βρίσκονται σε απροσδιόριστες κβαντικές καταστάσεις· και επίσης, ότι υπάρχουν κλασικά αντικείμενα, όπως οι γάτες, που μπορεί να βρίσκονται μόνο σε κλασικές καταστάσεις. To πρόβλημα γίνεται αντιληπτό αμέσως μόλις σκεφτούμε ότι μια γάτα απαρτίζεται από κβαντικά συστατικά στοιχεία — πρωτόνια, νετρόνια και ηλεκτρόνια. Εφόσον, λοιπόν, δεχόμαστε ότι η κβαντική θεωρία αποτελεί τη θεμελιώδη βάση όλης της φυσικής, τότε πώς είναι δυνατόν μια γάτα να εμφανίζεται ως κλασική, αναμφισβήτητα νεκρή ή ζωντανή γάτα, παρά ως κβαντική μισονεκρή-μισοζωντανή γάτα;

Μια διαφορετική προσέγγιση της μισονεκρής – μισοζωντανής γάτας

Ιδού, λοιπόν, ένας διαφορετικός τρόπος για να προσεγγίσουμε το πρόβλημα της μέτρησης. Σε ποιο σημείο της αλυσίδας των συμβάντων, από το φωτόνιο που προσπίπτει στο φίλτρο και ανιχνεύεται έως το φιαλίδιο με το δηλητήριο που σπάει και σκοτώνει ή όχι τη γάτα, γίνεται στην πραγματικότητα η μέτρηση; Πού παραχωρεί τη θέση της η κβαντική απροσδιοριστία στην κλασική προσδιοριστικότητα, και με ποιον τρόπο;

Το βασικό ζήτημα περιστρέφεται γύρω από το τι σημαίνει να μιλάμε για μια κβαντική κατάσταση ενός σύνθετου αντικειμένου όπως η γάτα. H ιδιότητα του ζωντανού ή νεκρού δεν αποτελεί εσωτερική ιδιότητα των στοιχειωδών κβαντικών συστατικών της γάτας αλλά μάλλον συλλογική ιδιότητα του τρόπου με τον οποίο συναρθρώνονται όλα αυτά τα συστατικά. Μια κβαντική κατάσταση της γάτας, που περιγράφεται πλήρως, θα σήμαινε τον ακριβή και πλήρη καθορισμό της κβαντικής κατάστασης του καθενός από τα ξεχωριστά σωματίδια της γάτας. Και ένα μόνο ηλεκτρόνιο να μεταβεί σε διαφορετική κατάσταση, ολόκληρη η γάτα συλλογικά μεταπίπτει σε διαφορετική ολική κβαντική κατάσταση.

Προφανώς, υπάρχουν αναρίθμητες (σχεδόν) κβαντικές καταστάσεις που αντιστοιχούν όλες στην ίδια γάτα. Ακόμη και όταν η γάτα φαίνεται να μην κάνει απολύτως τίποτε, όπως άλλωστε συνηθίζουν αυτά τα συμπαθή αιλουροειδή, η εσωτερική της κβαντική δομή βρίσκεται σε συνεχή αναταραχή, μεταβαίνοντας από τη μία κατάσταση στην άλλη. Πάντως, όλες οι κβαντικές καταστάσεις της γάτας πρέπει να ανήκουν σε μία απ’ τις εξής δύο κατηγορίες: σε αυτές που αντιστοιχούν σε ζωντανές γάτες και σε εκείνες που παριστούν νεκρές γάτες.

Εν τοιαύτη περιπτώσει, μπορούμε να κατασκευάσουμε μια πραγματική κβαντική κατάσταση όπου η γάτα να είναι μισονεκρή – μισοζωντανή; Θεωρητικά, ναι. Αρκεί να επιλέξουμε μία κατάσταση από το σύνολο των κβαντικών καταστάσεων που αντιστοιχούν στη νεκρή γάτα και μία άλλη από το σύνολο των κβαντικών καταστάσεων που αντιστοιχούν στη ζωντανή γάτα και, με τη συνήθη διαδικασία, να τις συνδυάσουμε μαθηματικά σε μία μοναδική κατάσταση που μετέχει εξίσου των δύο δυνατοτήτων. Είναι το ίδιο πράγμα, αν και σε πολύ μεγαλύτερη κλίμακα, σαν να συνδυάζαμε κβαντικές καταστάσεις φωτονίων με οριζόντια και κατακόρυφη πόλωση έτσι ώστε να προκύψει ένα φωτόνιο σε μια απροσδιόριστη κατάσταση, που η πόλωση του μένει να μετρηθεί.

Μια «μισοοριζόντια και μισοκατακόρυφη» κατάσταση πόλωσης ενός φωτονίου θα παραμείνει ως έχει. Κατ’ αρχήν, το ίδιο ισχύει και για μια «μισοζωντανή- μισονεκρή» κβαντική κατάσταση της γάτας. Εδώ, όμως, τα πράγματα περιπλέκονται. Και τούτο επειδή τόσο το ζωντανό μισό της γάτας όσο και το νεκρό είναι ελεύθερα να εξελιχθούν γρήγορα σε μια από τις μυριάδες άλλες καταστάσεις ζωής και θανάτου στις οποίες επιτρέπεται να μεταπέσουν. Το σπουδαιότερο δε, καθώς το νεκρό μέρος «σαρώνει» ταχύτατα όλες τις δυνατές καταστάσεις θανάτου και το ίδιο κάνει και το ζωντανό μισό, τα δύο μισά εξελίσσονται το ένα ανεξάρτητα από το άλλο.

Για να παρουσιάσουμε μια πραγματική «μισονεκρή-μισοζωντανή» κατάσταση, θα πρέπει να επιτευχθεί μια πολύ συγκεκριμένη συνεκτικότητα στον τρόπο με τον οποίο οι δύο συνιστώσες συνδυάζονται μεταξύ τους. Καθώς κάθε συνιστώσα εξελίσσεται, αυτή η συνεκτικότητα καταστρέφεται, οπότε στην πράξη η γάτα δεν συμπεριφέρεται σαν να είναι «μισοζωντανή-μισόνεκρή» αλλά σαν να είναι ή ζωντανή ή νεκρή, δηλαδή ακριβώς όπως περιμένουμε να συμπεριφέρεται μια γάτα. Για να ακριβολογούμε, δεν σημειώθηκε κάποια θεμελιώδης μεταβολή του συστήματος κατά το πέρασμα από την κατάσταση «ζωής και θανάτου» σε εκείνη της «ζωής ή θανάτου»· απλώς, καθίσταται πρακτικά αδύνατη η πραγματοποίηση ενός πειράματος όπου θα παρατηρηθεί οτιδήποτε εκτός από μια γάτα που είναι ή νεκρή ή ζωντανή. Από πρακτική άποψη, λοιπόν, η γάτα είναι κλασική.

H διαδικασία αυτή της «άρσης της συνεκτικότητας» μεταξύ των συνιστωσών μιας σύνθετης κβαντικής κατάστασης καταδεικνύει πόσο δύσκολο είναι να διατηρήσουμε σύνθετα αντικείμενα σε καθαρές κβαντικές καταστάσεις. Και τούτο επειδή αυτά τα αντικείμενα υπόκεινται σε αναρίθμητες τυχαίες αλληλεπιδράσεις και επιδράσεις, τόσο εσωτερικές όσο και εξωτερικές. Ev ολίγοις, δεν είναι αδύνατο να υπάρξει μια «μισονεκρή-μισοζωντανή» γάτα* είναι απλώς εξαιρετικά απίθανο —και σχεδόν αδύνατο να ανιχνευθεί.

Υπάρχει και ένας εναλλακτικός τρόπος για να συλλάβουμε αυτή την κατάσταση: μπορούμε να πούμε ότι η συνεχής αλληλεπίδραση των ατόμων και των ηλεκτρονίων της γάτας ισοδυναμεί με μια διαρκή «αυτομέτρηση» της κβαντικής κατάστασης. Δεν είναι η παρατήρηση ή η ανίχνευση αλλά η ακατάπαυστη αλληλεπίδραση όλων των κβαντικών καταστάσεων σε μια γάτα που παρεμποδίζει κάθε ξεχωριστή κατάσταση να παραμείνει σταθερή.

Έτσι, οι άνθρωποι ή οι γάτες θα βρεθούν αναπόφευκτα σε μια παρατηρήσιμη κλασική κατάσταση — έστω και αν η υποκείμενη κβαντική κατάσταση της γάτας μεταβάλλεται ακατάπαυστα και είναι ολωσδιόλου απρόβλεπτη. Με άλλα λόγια, μπορεί να θεωρείται βέβαιο ότι καθετί μεγάλο θα φαίνεται, σχεδόν πάντα, ως κλασικό και όχι ως κβαντικό αντικείμενο. Ακριβώς σύμφωνα με τους κανόνες που θέσπισε ο δόκτωρ Bohr!

Συγγραφέας του άρθρου είναι ο David Lindley ένας θεωρητικός φυσικός του Πανεπιστημίου του Κέμπριτζ και των Εργαστηρίων FERMI. Θεωρείται από τους καλύτερους εκλαϊκευτές της Φυσικής (από το περιοδικό Quantum)