1. Εισαγωγή Η συμμετρία στη Φύση – H νιφάδα του χιονιού
H έννοια της συμμετρίας ξεκίνησε από την εποχή του Πυθαγόρα, ο οποίος πίστευε ότι πίσω από την πολυπλοκότητα των καθημερινών γεγονότων ο κόσμος έχει μια αρμονία και ότι τα μαθηματικά είναι η γλώσσα με την οποία αυτή η αρμονία εκφράζεται.
Όταν λοιπόν κάποιος δει στο μικροσκόπιο μια νιφάδα του χιονιού θα θαυμάσει το συμμετρικό σχήμα της. Πρόκειται για ένα μικροσκοπικό εξαγωνικό κρύσταλλο, που αποτελείται από έξι σχεδόν όμοια πέταλα. Έτσι αν τον περιστρέψουμε κατά 60 ή κατά 120 μοίρες γύρω από το κέντρο του θα φαίνεται ακριβώς όμοιος. O κρύσταλλος δηλαδή παραμένει αναλλοίωτος κάτω από έναν τέτοιο μετασχηματισμό περιστροφής, γεγονός που χαρακτηρίζει τη συμμετρία του.
Σύμφωνα τώρα με τον μαθηματικό Weyl ένα αντικείμενο είναι συμμετρικό, αν υπάρχει μια διαδικασία η οποία αφήνει αναλλοίωτη τη μορφή του.
Σύμφωνα με τον παραπάνω ορισμό συμμετρία στους νόμους της Φυσικής σημαίνει ότι μπορούμε να κάνουμε τέτοιες αλλαγές στα μεγέθη που υπεισέρχονται στους νόμους, οι οποίες να μην επιφέρουν καμιά τροποποίηση στους νόμους και τα αποτελέσματά τους.
Κατ’ αρχήν πρέπει να πούμε πως οι νόμοι της φύσης είναι παντού ίδιοι. Δεν παρατηρούμε καμία διαφορά στα αποτελέσματα ενός πειράματος όταν αυτό πραγματοποιείται σε διαφορετικά σημεία στο χώρο.
Ένα πολύ απλό παράδειγμα αυτού του είδους συμμετρίας είναι η μετατόπιση στο χώρο: Οι νόμοι της Φυσικής παραμένουν αναλλοίωτοι σε μετατοπίσεις στο χώρο. Επίσης, παραμένουν αναλλοίωτοι σε περιστροφές γύρω από οποιονδήποτε άξονα που περνάει από κάποιο σημείο.
Πώς όμως περιγράφεται με μαθηματικό τρόπο; Έστω λοιπόν ένα αντικείμενο στο χώρο δύο διαστάσεων. Ένας παρατηρητής για να βρει τη θέση του ορίζει αυθαίρετα ένα σύστημα συντεταγμένων, έστω A, και στο σύστημα αυτό η θέση του αντικειμένου προσδιορίζεται από τις συντεταγμένες Χ, Υ και η απόσταση του δίνεται από την σχέση Χ2+Υ2. Εφόσον όμως το σύστημα συντεταγμένων είναι αυθαίρετο, ο παρατηρητής θα μπορούσε να χρησιμοποιήσει ένα οποιοδήποτε άλλο, έστω B, το οποίο για παράδειγμα να έχει διαφορετικό προσανατολισμό ως προς το A. Σε αυτό το σύστημα B οι συντεταγμένες του σημείου θα είναι προφανώς διαφορετικές, έστω Χ’ και Υ’. H δε απόσταση του με βάση τις νέες συντεταγμένες θα είναι Χ‘2+Υ‘2.
Ωστόσο, οι νόμοι της Φυσικής θα πρέπει να εκφράζονται με τέτοιο τρόπο ώστε να μην αλλάζουν μορφή όταν υπόκεινται στον παραπάνω μετασχηματισμό. Δηλαδή, εδώ η απόσταση του (που είναι κάτι το αντικειμενικό) θα είναι ίδια σε όλα τα συστήματα συντεταγμένων, ανεξάρτητα από το αν το δεύτερο είναι στραμμένο ως προς το πρώτο και ανεξάρτητο από κάθε σύστημα. Έτσι, παρόλο που έχουμε μετασχηματισμό περιστροφής ισχύει ότι η απόσταση S = Χ2+Υ2 = Χ‘2+Υ‘2.
Τι μας λέει όμως αυτή η συμμετρία: ότι δεν υπάρχει κανένα προνομιακό σημείο στο σύμπαν που να είναι η αρχή μέτρησης του χώρου. Όλα τα σημεία είναι ισοδύναμα και οι νόμοι της Φυσικής πρέπει να εκφράζονται με τέτοιο τρόπο ώστε να είναι αναλλοίωτοι σε μετασχηματισμούς περιστροφής και μετατόπισης. Ή για να το πούμε διαφορετικά: δεν πρέπει να παρατηρούμε καμία διαφορά στα αποτελέσματα ενός πειράματος όταν αυτό πραγματοποιείται σε διαφορετικά σημεία στο χώρο.
2. Η κρυμμένη συμμετρία στο νόμο της παγκόσμιος έλξης του Νεύτωνα
Τον 16ο αιώνα οι άνθρωποι θεωρούσαν ότι ο Θεός έχει φτιάξει ένα αρμονικό και συμμετρικό σύμπαν, με τέλεια σχήματα (όπως ο κύκλος ή η σφαίρα), απαλλαγμένο από μη συμμετρικά σχήματα (ελλείψεις ή περίπλοκα σχήματα). Όμως η αντίληψη αυτή οδήγησε σε λάθος θεωρήσεις, όπως για παράδειγμα οι άνθρωποι αρνιόντουσαν να δουν τις ελλειπτικές τροχιές των πλανητών γύρω από τον Ήλιο. Έτσι, προσπαθούσαν να εξηγήσουν τις κινήσεις των πλανητών με την ιδέα ότι εφόσον το σύμπαν είναι συμμετρικό (τέλειο – θεϊκό), θα πρέπει οι πλανήτες, ο Ήλιος, το φεγγάρι και τα αστέρια να κινούνται σε τέλειες κυκλικές τροχιές, με την Γη (το κέντρο της Δημιουργίας) ακριβώς στο κέντρο αυτών των κυκλικών τροχιών. Φυσικά τότε το μοντέλο του Πτολεμαίου ικανοποιούσε την αισθητική και την αντίληψη του για το θείο. O Θεός σύμφωνα με τον Πτολεμαίο έπρεπε να έχει δημιουργήσει ένα κομψό, ένα συμμετρικό σύμπαν, με τέλειες κυκλικές τροχιές ή επίκυκλων στο κέντρο των οποίων ήταν κι ένας πλανήτης.
Στη φύση όμως δεν υπάρχουν προνομιακά σημεία στο σύμπαν (όπως θεωρούσε τότε ο Πτολεμαίος για τη Γη) και αυτό σημαίνει ότι οι νόμοι της φύσης πρέπει να εκφράζονται έτσι, ώστε να είναι αναλλοίωτοι σε περιστροφές. Αν υπήρχε κάποιο προνομιακό σημείο στο σύμπαν θα έπαυε να υπάρχει συμμετρία στο σύμπαν – άτοπον.
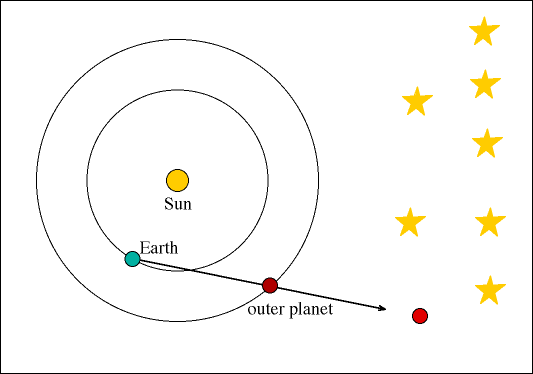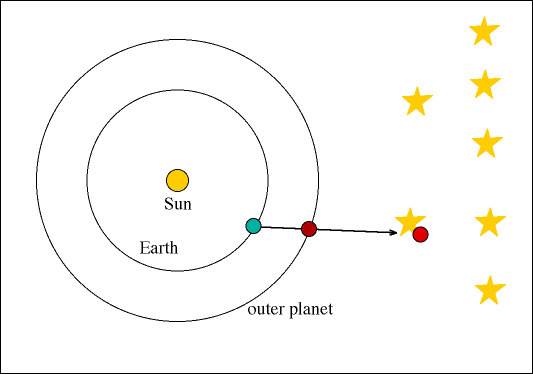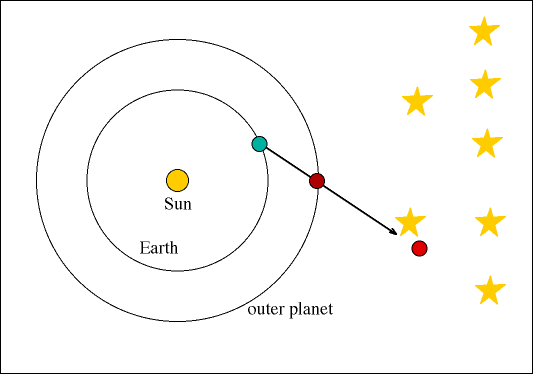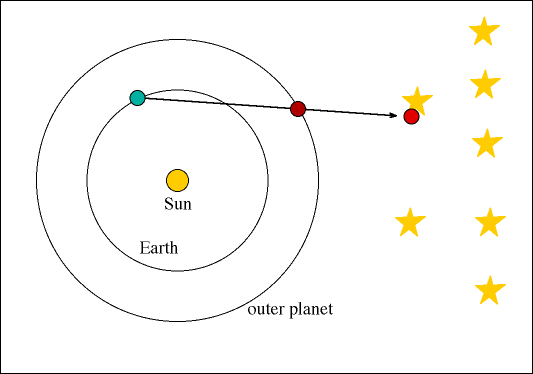
Το ηλιοκεντρικό μοντέλο του Κοπέρνικου με τις κυκλικές τροχιές
Ο Κοπέρνικος υιοθέτησε μεν την ιδέα του Αρίσταρχου, το ηλιοκεντρικό μοντέλο, οπότε οι πλανήτες θεώρησε ότι κινούνται γύρω από τον Ήλιο, αλλά πάλι σε κυκλικές τροχιές. Δηλαδή το προνομιακό σημείο μεταφέρθηκε από τη Γη στον Ήλιο.
Έναν αιώνα αργότερα ο Γιόχαν Κέπλερ έκανε το επόμενο μεγάλο άλμα θεωρώντας ότι οι κινήσεις των πλανητών δεν είναι κυκλικές αλλά ελλειπτικές (πρώτος νόμος του Κέπλερ). Ένα σχήμα δηλαδή που δεν παρουσιάζει την τελειότητα και τη συμμετρία του κύκλου, όπως το θεωρούσαν μέχρι τότε. Όμως ο κύκλος (το πιο απλό σχήμα στον χώρο) δεν αντιπροσωπεύει και την αληθινή συμμετρία που χαρακτηρίζει τον κόσμο. Φυσικά είναι δύσκολο να αντιληφθεί κάποιος ότι η έλλειψη κι όχι ο κύκλος εμπεριέχει μια συμμετρία, κι αυτό φαίνεται στον δεύτερο νόμο του Κέπλερ που έχει σχέση με τη ταχύτητα των πλανητών γύρω από τον Ήλιο. Διαπίστωσε λοιπόν ότι τα εμβαδά που διαγράφουν οι επιβατικές ακτίνες των πλανητών είναι ίσα, σε ίσους χρόνους. Για να είναι αυτά τα εμβαδά ίσα θα πρέπει ο πλανήτης να κινείται ταχύτερα όταν βρίσκεται κοντύτερα στον Ήλιο και πιο αργά όταν βρίσκεται μακρύτερα.
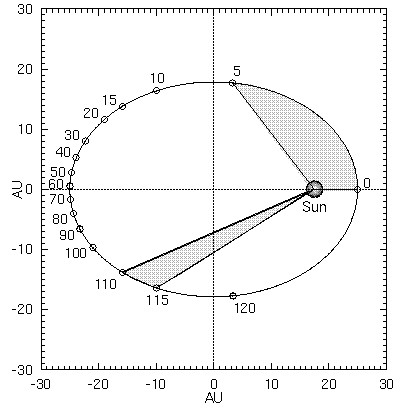
Ο 2ος νόμος του Κέπλερ: η Γη διαγράφει μια έλλειψη γύρω από τον Ήλιο, ο οποίος βρίσκεται στη μία εστία της έλλειψης. Παρατηρούμε ότι η επιβατική ακτίνα που ξεκινάει από τον Ήλιο και φθάνει στη Γη σε ίσους χρόνους διαγράφει ίσα εμβαδά
Σήμερα ξέρουμε ότι ο νόμος αυτός εκφράζει τη διατήρηση της στροφορμής. Η στροφορμή είναι ακριβώς το εμβαδό που διαγράφεται από ένα σώμα το οποίο περιστρέφεται. H στροφορμή ενός πλανήτη είναι το μέτρο της τροχιακής του κίνησης και αυτό δεν θα πρέπει να αλλάζει καθώς ο πλανήτης περιστρέφεται γύρω από τον Ήλιο. Για να διατηρείται αυτό το μέγεθος σταθερό (η στροφορμή ή το εμβαδόν δηλαδή) θα πρέπει όταν η απόσταση μικραίνει η ταχύτητα να μεγαλώνει και το αντίστροφο. Το γεγονός λοιπόν ότι οι πλανήτες κινούνται σε ελλειπτικές τροχιές και αλλάζουν ταχύτητα ανάλογα με τη απόσταση τους δεν είναι μια «παραξενιά» της φύσης αλλά εκφράζει τη συμμετρία σε περιστροφές στο χώρο, συμμετρία άμεσα συνδεδεμένη με τη διατήρηση της στροφορμής.
Κατά τη διάρκεια των αιώνων που πέρασαν, οι μαθηματικοί και οι φυσικοί άρχισαν να αντιλαμβάνονται ότι υπάρχει μια βαθειά σχέση μεταξύ συμμετρίας και νόμων διατήρησης στη Φυσική. H διατήρηση της ορμής σχετίζεται με τη συμμετρία σε μετατοπίσεις. H διατήρηση της στροφορμής σχετίζεται με τη συμμετρία σε περιστροφές. Και η διατήρηση της ενέργειας είναι αποτέλεσμα του αναλλοίωτου των νόμων της Φυσικής σε μετατοπίσεις στο χρόνο.
Αλλά και ο νόμος βαρύτητας του Νεύτωνα, που δέχεται ότι όλα τα σώματα αλληλεπιδρούν μεταξύ τους με μια δύναμη αντιστρόφως ανάλογη με το τετράγωνο της απόστασης τους, δεν εξαρτάται από το σύστημα αναφοράς αλλά μόνο από τις μάζες και τις σχετικές αποστάσεις των σωμάτων. Ισχύει τόσο για σώματα πάνω στη Γη όσο και για τις κινήσεις των πλανητών γύρω από τον Ήλιο. Είναι συνεπώς αναλλοίωτος σε μετατοπίσεις και περιστροφές. Επιπλέον εμπεριέχει τους νόμους του Κέπλερ και ταυτόχρονα περιγράφει την έλξη των σωμάτων από τη Γη: δεν υπάρχουν διαφορετικοί νόμοι που να περιγράφουν αυτό που συμβαίνει στη Γη και αυτό που συμβαίνει στον ουρανό. Βλέπουμε λοιπόν ότι ο νόμος βαρύτητας του Νεύτωνα εκφράζει τη συμμετρία που υπάρχει στη φύση, είναι αναλλοίωτος σε μετασχηματισμούς περιστροφής και μετατόπισης.
Αυτή η σχέση μεταξύ συμμετρίας και νόμων διατήρησης εδραιώθηκε με το μαθηματικό τύπο που είναι γνωστός σαν θεώρημα Noether. Οι νόμοι της Κλασσικής Φυσικής μπορούν να προκύψουν από το θεώρημα της ελάχιστης δράσης. H μαθηματικός Emmy Noether (1918) έδειξε ότι κάθε τέτοιος νόμος που παρουσιάζει μια συμμετρία συνοδεύεται από μια διατηρούμενη ποσότητα, η οποία μπορεί να προκύψει από το θεώρημα ελάχιστης δράσης.
3. Η συμμετρία στην σχετικότητα του Γαλιλαίου
H διατύπωση της Αρχής της Σχετικότητας του Γαλιλαίου λέει ότι οι νόμοι της Φυσικής παραμένουν ίδιοι, ανεξάρτητοι από το αν είμαστε ακίνητοι η κινούμαστε με σταθερή ταχύτητα πάνω σε ευθεία γραμμή, δηλαδή είναι ίδιοι για κάθε αδρανειακό παρατηρητή. Αν λοιπόν ταξιδεύουμε σε ένα αεροπλάνο που κινείται με σταθερή ταχύτητα σε σχέση με τη Γη, τα πάντα μέσα στο αεροπλάνο συμπεριφέρονται με τον ίδιο τρόπο ως εάν ήμασταν ακίνητοι κάτω στη Γη. Τι σημαίνει ακριβώς αυτή η συμμετρία; Σημαίνει ότι ένας αδρανειακός παρατηρητής δεν μπορεί από το αποτέλεσμα πειραμάτων να διακρίνει μια κατάσταση ηρεμίας από μια κατάσταση σταθερής κίνησης σε ευθεία γραμμή.
Αριστερά βλέπουμε το σύστημα αναφοράς του κόκκινου οδηγού που είναι το ίδιο με το δικό μας, όταν στεκόμαστε ακίνητοι στην άκρη του δρόμου. Ως προς αυτό το σύστημα αναφοράς, το μπλε αυτοκίνητο ταξιδεύει προς τα εμπρός με ταχύτητα Uμπλε και κάποια αντικείμενα (πχ μπάλες) πετιούνται από το μπλε αυτοκίνητο με ταχύτητα V όπως την αντιλαμβάνεται ο παρατηρητής στο κόκκινο αυτοκίνητο.
Δεξιά διευκρινίζεται τι συμβαίνει, ως προς το σύστημα αναφοράς του μπλε αυτοκινήτου. Ως προς το μπλε αυτοκίνητο, λοιπόν, τα αντικείμενα πετιούνται προς τα εμπρός από το παράθυρό του με ταχύτητα V’ και το κόκκινο αυτοκίνητο πηγαίνει προς τα πίσω
Μέχρι όμως την εποχή του Νεύτωνα οι άνθρωποι πίστευαν στον απόλυτο χώρο. Ότι όλοι μας ανεξαρτήτως εάν κινούμαστε ή όχι, τον αντιλαμβανόμαστε με τον ίδιο τρόπο. Ένα αντικείμενο ή ένα γεγονός έχει μια θέση στον απόλυτο χώρο και όλοι μας συμφωνούμε για τη θέση αυτή. Σύμφωνα όμως με την αρχή της σχετικότητας του Γαλιλαίου η έννοια του απόλυτου χώρου, δηλαδή της απόλυτης θέσης ενός αντικειμένου ή ενός γεγονότος στο χώρο καταργείται. Γιατί μπορεί ο ταξιδιώτης μέσα στο αεροπλάνο να αντιλαμβάνεται μόνο την κίνηση του μέσα στο αεροπλάνο, αλλά ένας παρατηρητής στη Γη θα πει πως αφού το αεροπλάνο κινείται ως προς τη Γη συμμετέχει σε δύο κινήσεις ταυτόχρονα, άρα η θέση του στον χώρο (όπως την καταλαβαίνει ο παρατηρητής στη Γη), αλλάζει και λόγω της κίνησης του ταξιδιώτη μέσα στο αεροπλάνο και λόγω της κίνησης του ίδιου του αεροπλάνου. Άρα οι δύο τους (ταξιδιώτης και παρατηρητής στη Γη) διαφωνούν ως προς το ποια είναι η θέση ενός αντικειμένου ή ενός γεγονότος στο χώρο και την ορίζουν βάσει του συστήματος αναφοράς που χρησιμοποιούν. Όμως και οι δύο περιγραφές στο παραπάνω παράδειγμα είναι σωστές, και δεν υπάρχει σωστό και λάθος σύστημα αναφοράς στη φύση.
Το σύστημα αναφοράς είναι ένα ανθρώπινο εργαλείο που το χρησιμοποιούμε για να ορίσουμε τη θέση ενός αντικειμένου ή γεγονότος. Ωστόσο η φυσική πραγματικότητα είναι ανεξάρτητη από το σύστημα αναφοράς που χρησιμοποιούμε για να την περιγράψουμε, είναι ίδια για όλα τα συστήματα αναφοράς. Συνέπεια λοιπόν της συμμετρίας που διέπει το φυσικό μας κόσμο όσον αφορά στην κίνηση με σταθερή ταχύτητα σε ευθεία γραμμή (όπου συμμετρία σημαίνει ότι δεν μπορείς να πεις τίνος παρατηρητή η άποψη είναι σωστή) είναι ότι όταν συζητάμε για αντικείμενα ή γεγονότα που συμβαίνουν σ’ ένα σημείο του χώρου αυτό είναι άνευ σημασίας. Το πού συμβαίνει ένα γεγονός εξαρτάται από την ταχύτητα με την οποία κινούμαστε, ωστόσο οι νόμοι της φύσης είναι ανεξάρτητοι από αυτήν την κίνηση. Για να μετατρέψουμε τη μία συντεταγμένη του γεγονότος (όπως τη βλέπει ο ένας παρατηρητής) στην συντεταγμένη του άλλου παρατηρητή (αν κινείται με σταθερή ταχύτητα ως προς τον πρώτο) χρησιμοποιούμε κάποιες μαθηματικές εξισώσεις, που λέγονται μετασχηματισμοί του Γαλιλαίου.
Βλέπουμε λοιπόν ότι η έννοια του απόλυτου χώρου του Αριστοτέλη είναι ασυμβίβαστη με την Αρχή της Σχετικότητας του Γαλιλαίου. Ωστόσο παραμένει η έννοια του απόλυτου χρόνου. Ο χρόνος εξακολουθούσε μέχρι το 1905 να ήταν παγκόσμιος και απόλυτος, όμως τότε καταρρίφθηκε από τον Αϊνστάιν.
4. Η συμμετρία στην Ειδική θεωρία της Σχετικότητας
Πέρασαν περίπου 200 χρόνια από τότε που ο Γαλιλαίος διατύπωσε την Αρχή της Σχετικότητας ώσπου το 1873 ο James Clerk Maxwell δημοσίευσε ένα σύνολο εξισώσεων, οι οποίες περιγράφουν τους νόμους του ηλεκτρομαγνητισμού. Μία από τις πιο δραματικές συνέπειες των εξισώσεων του Maxwell ήταν ότι το φως είναι ένα ηλεκτρομαγνητικό κύμα το οποίο ταξιδεύει με σταθερή ταχύτητα c ίση με 300 χιλιάδες χιλιόμετρα το δευτερόλεπτο. Το ερώτημα που προέκυψε αμέσως ήταν: σταθερή ταχύτητα σε σχέση με τι; H επιστημονική κοινότητα της εποχής υιοθέτησε την εξήγηση ότι τα κύματα του φωτός είναι ταλαντώσεις ενός υποθετικού μέσου (του αιθέρα), που καλύπτει όλο το χώρο, όπως ακριβώς τα ηχητικά κύματα είναι ταλαντώσεις του αέρα και τα κύματα του νερού είναι ταλαντώσεις στην επιφάνεια ενός υγρού σώματος. Το φως συνεπώς ταξιδεύει με ταχύτητα c σε σχέση με τον αιθέρα, σε σχέση δηλαδή μ’ ένα Ακίνητο Σύστημα Αναφοράς (Α.Σ.Α) το οποίο είναι ακίνητο ως προς τον αιθέρα. Τότε όμως, σύμφωνα με την αρχή σχετικότητας του Γαλιλαίου, για ένα Α.Σ.Α που κινείται ως προς τον αιθέρα η ταχύτητα του φωτός θα πρέπει να είναι διαφορετική. Κάτι αντίστοιχο λοιπόν θα έπρεπε να ισχύει και για τη Γη. H Γη κινείται μέσα στον απόλυτο αιθέρα και περιφέρεται γύρω από τον Ήλιο. Τον Ιανουάριο κινείται προς μια κατεύθυνση και ύστερα από έξι μήνες προς την αντίθετη κατεύθυνση. Συνεπώς θα πρέπει πάνω στη Γη να μετράμε διαφορετική ταχύτητα του φωτός σε διαφορετικές κατευθύνσεις και η διαφορά αυτή θα πρέπει να μεταβάλλεται με τις εποχές. H επαλήθευση μιας τέτοιας πρόβλεψης ήταν μια πραγματική πρόκληση για εκείνη την εποχή. Οι Michelson και Morley ανέλαβαν να την επιβεβαιώσουν πραγματοποιώντας, το 1881, το ομώνυμο πείραμα, το οποίο ωστόσο δεν μπόρεσε να βρει καμία ένδειξη ότι η ταχύτητα του φωτός μεταβάλλεται με την κατεύθυνση. Τι λοιπόν συνέβαινε; Ήταν το πείραμα λάθος; Ήτανε οι νόμοι του Maxwell λάθος ή λάθος οι μετασχηματισμοί ταχύτητας του Γαλιλαίου;
H λύση του προβλήματος δόθηκε όταν ο Einstein και ο Poincare συνειδητοποίησαν ότι ο μόνος τρόπος με τον οποίο είναι δυνατόν κάποιος που κινείται και κάποιος που δεν κινείται να μετρούν την ίδια ταχύτητα είναι να έχουν διαφορετική αντίληψη όχι μόνο για το χώρο αλλά και για το χρόνο. Αυτό σημαίνει ότι ο χρόνος παύει να είναι απόλυτος, ίδιος για όλους τους αδρανειακούς παρατηρητές. H ιδέα αυτή αποτελεί την ουσία της Ειδικής θεωρίας της Σχετικότητας της οποίας η διατύπωση είναι η εξής:
1. Όλοι οι νόμοι της Φυσικής είναι ίδιοι για κάθε αδρανειακό παρατηρητή.
2. H ταχύτητα του φωτός είναι σταθερή για όλους τους αδρανειακούς παρατηρητές, όπως υποδηλώνει το πείραμα.
Ας δούμε όμως πώς είδε ο Αϊνστάιν την σχετικότητα
Πάρτε τα κόκκινα και μπλε αυτοκίνητα από το προηγούμενο παράδειγμα, και βάλτε ένα λέιζερ πάνω στο μπλε αυτοκίνητο. Θα βάλουμε έναν καθρέφτη στο μπλε αυτοκίνητο όπως φαίνεται στα σχήματα, και θα στοχεύσουμε με το λέιζερ στον καθρέπτη κάθετα στη κατεύθυνση που το μπλε αυτοκίνητο ταξιδεύει.
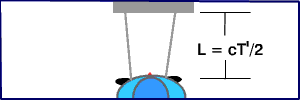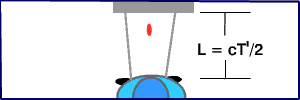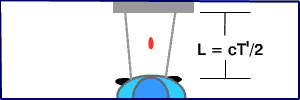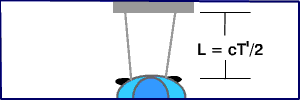
Η διαδρομή του παλμού του λέιζερ όπως εμφανίζεται στο σύστημα αναφοράς του μπλε αυτοκινήτου.
Μέσα στο χρονικό διάστημα T που μετρείται από τον οδηγό του μπλε αυτοκινήτου, ο οποίος ενεργοποιεί το λέιζερ, το φως του λέιζερ ταξιδεύει μια απόσταση 2L, από το λέιζερ στον καθρέφτη και πάλι πίσω.
Εν τω μεταξύ, η οδηγός του κόκκινου αυτοκινήτου βλέπει το μπλε αυτοκίνητο που πλησιάζει. Σύμφωνα με την οδηγό του κόκκινου αυτοκινήτου, το λέιζερ χρειάστηκε έναν συνολικό χρόνο Τ για να χτυπήσει τον καθρέφτη και να επιστρέψει. (Αυτή η οδηγός είναι πρόθυμη να συμφωνήσει με την οδηγό του μπλε αυτοκινήτου ότι η απόσταση μεταξύ του λέιζερ και του καθρέφτη είναι L, δεδομένου ότι κανένας οδηγός δεν έχει οποιαδήποτε ταχύτητα προς εκείνη την κατεύθυνση, αφού κινούνται κάθετα προς αυτήν)
Η οδηγός του κόκκινου μετρά ότι το μπλε αυτοκίνητο έχει ταξιδέψει μια απόσταση X=Uμπλε.T και ο παλμός του λέιζερ ότι έχει ταξιδέψει μια συνολική απόσταση 2D=CT στο χρόνο αυτό (όπου C=ταχύτητα του φωτός)
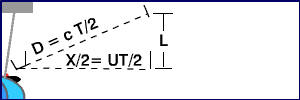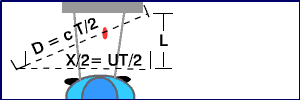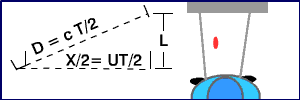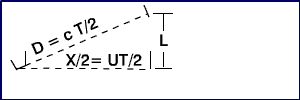
Εδώ είναι ο παλμός του λέιζερ όπως εμφανίζεται στο σύστημα αναφοράς του κόκκινου αυτοκινήτου.
Εδώ είναι που προκύπτει το πρόβλημα. Δεδομένου όπως συναγάγαμε ακριβώς πιο πάνω, ότι cT’ = 2L και cT = 2D, ο μόνος τρόπος που θα μπορούσαμε να είχαμε ίσους χρόνους T’ = T θα ήταν αν η απόσταση D = L.
Επομένως, οι οδηγοί του κόκκινου και μπλε αυτοκινήτου δεν αντιλαμβάνονται τα χρονικά διαστήματα μεταξύ εκπομπής και λήψης του παλμού ως ίσα.
Έτσι δύο γεγονότα που είναι ταυτόχρονα σε ένα σύστημα αναφοράς, δεν είναι κατ’ ανάγκη ταυτόχρονα και σε ένα άλλο, που κινείται ως προς το πρώτο. Ή διαφορετικά: γεγονότα που είναι ταυτόχρονα για έναν αδρανειακό παρατηρητή που κινείται δεν είναι ταυτόχρονα για έναν ακίνητο παρατηρητή και το αντίστροφο.
Αυτή είναι μια βασική διαφορά ανάμεσα στο μοντέλο του Αϊνστάιν και στο Νευτώνειο μοντέλο.
Γιατί υπάρχει αυτή η διαφορά στο χρόνο; H απάντηση είναι ότι τα γεγονότα αυτά απέχουν χωρικά και όπως ξέρουμε οι χωρικές συντεταγμένες ενός γεγονότος εξαρτώνται από το σύστημα αναφοράς που χρησιμοποιούμε για να τις ορίσουμε. Άρα λοιπόν μια από τις συνέπειες της συμμετρίας όσον αφορά στην κίνηση με σταθερή ταχύτητα σε ευθεία γραμμή (όπου συμμετρία σημαίνει ότι δεν μπορούμε να πούμε τίνος η άποψη είναι σωστή) είναι πως το να αναφερόμαστε σε γεγονότα που συμβαίνουν στον κόσμο «τώρα» είναι άνευ σημασίας, αν τα γεγονότα απέχουν χωρικά. Προφανώς το ταυτόχρονο δεν ταυτίζεται για τους δύο παρατηρητές.
Το γεγονός αυτό το είδαμε και στην σχετικότητα του Γαλιλαίου όπου δεν ταυτίζονταν οι συντεταγμένες ενός γεγονότος, γιατί το ένα σύστημα κινούνταν ως προς το άλλο: διαφορετικοί παρατηρητές ανάλογα με το αν κινούνται ή όχι έχουν διαφορετική άποψη για τη θέση ενός γεγονότος στο χώρο.
Αντίστοιχα λοιπόν δύο γεγονότα που για έναν αδρανειακό παρατηρητή φαίνεται να συμβαίνουν την ίδια χρονική στιγμή (ίδια χρονική συντεταγμένη t) για έναν άλλον αδρανειακό παρατηρητή συμβαίνουν σε διαφορετικές χρονικές στιγμές (διαφορετικές χρονικές συντεταγμένες). Σύμφωνα με την Ειδική θεωρία της Σχετικότητας κάθε γεγονός έχει μια χωρική συντεταγμένη (ουσιαστικά τρεις: x,y και z) και μια χρονική συντεταγμένη (t). O χώρος και ο χρόνος δηλαδή αλληλοσυμπλέκονται πλήρως σε μια νέα οντότητα μέσα στην οποία ζούμε, τον τετραδιάστατο χωρόχρονο. Χρειαζόμαστε φυσικά έναν τρόπο με τον οποίο να «μεταφράζουμε» τις χωροχρονικές συντεταγμένες ενός γεγονότος μετρημένες σ’ ένα ακίνητο σύστημα αναφοράς (Α.Σ.Α) σε χωροχρονικές συντεταγμένες σ’ ένα άλλο Α.Σ.Α που κινείται με σταθερή ταχύτητα σε σχέση με το πρώτο. Οι μαθηματικές εξισώσεις που κάνουν αυτή «τη μετάφραση» λέγονται μετασχηματισμοί Lorentz. Όλοι οι νόμοι της Φυσικής πρέπει να είναι αναλλοίωτοι κάτω από τους μετασχηματισμούς αυτούς, κατά αντιστοιχία με τους μετασχηματισμούς περιστροφής και τους μετασχηματισμούς του Γαλιλαίου, που είδαμε προηγουμένως.
Στους μετασχηματισμούς Lorentz διαπιστώνουμε τα γνωστά «παράξενα» και «εντυπωσιακά» της Ειδικής θεωρίας της Σχετικότητας αναφορικά με τη συστολή του μήκους και διαστολή του χρόνου. Ωστόσο δεν είναι και τόσο παράξενα αρκεί να σκεφτούμε ότι μήκος είναι η απόσταση μεταξύ δύο γεγονότων (δύο σημείων) που συμβαίνουν ταυτόχρονα. Ο λόγος λοιπόν που διαφορετικοί αδρανειακοί παρατηρητές μετρούν διαφορετικό μήκος είναι γιατί διαφωνούν ως προς το συγχρονισμό των δύο σημείων. Ο λόγος που μετρούν διαφορετικό χρόνο είναι γιατί διαφωνούν ως προς τη χωρική θέση των γεγονότων. H διαφωνία τους όμως είναι συμμετρική και συνεπώς κανείς δεν μπορεί να πει ποιανού η άποψη είναι η σωστή. Οι δύο περιγραφές είναι απόλυτα συμμετρικές. Δεν υπάρχει τίποτα παράδοξο στην Ειδική θεωρία της Σχετικότητας αρκεί να θεωρήσουμε ότι ο χρόνος δεν είναι απόλυτος όπως ήταν παραδεκτό μέχρι το 19° αιώνα.
Όπως αναφέραμε πριν κάθε συμμετρία είναι άμεσα συνδεδεμένη με τη διατήρηση ενός φυσικού μεγέθους (θεώρημα Noether). Στη Νευτώνεια Μηχανική η συμμετρία σε μετατοπίσεις και περιστροφές συνδέονται με τη διατήρηση της ενέργειας και της ορμής αντιστοίχως. Στη Σχετικιστική Φυσική μπορεί να δειχτεί ότι το μέγεθος που διατηρείται είναι η τετραορμή, ένα μέγεθος που έχει τρεις χωρικές και μια χρονική συντεταγμένη. Οι χωρικές συντεταγμένες της τετραορμής αντιστοιχούν στις χωρικές συντεταγμένες της ορμής, ενώ η χρονική λέγεται σχετικιστική ενέργεια και είναι το άθροισμα της μάζας και της κινητικής ενέργειας. H Ειδική θεωρία της Σχετικότητας όπως ακριβώς συνδέει το χρόνο και το χώρο σε μία γεωμετρία, έτσι συνδέει και τους νόμους διατήρησης της ενέργειας και της ορμής σ’ έναν νόμο, το νόμο διατήρησης της τετραορμής. Το γεγονός ότι διατηρείται η σχετικιστική ενέργεια σημαίνει ότι δεν διατηρείται χωριστά η μάζα και η ενέργεια, αλλά το άθροισμα τους. Συνεπώς μια διαδικασία στην οποία η μάζα γίνεται ενέργεια ή το αντίστροφο δεν παραβιάζει το νόμο διατήρησης της τετραορμής.
4. H ανακάλυψη νέων νόμων μέσω της αναζήτησης «κρυμμένων» συμμετριών
Η Αρχή της Ισοδυναμίας αναφέρει ότι η μάζα αδρανείας ενός σώματος είναι ίση με τη βαρυτική του μάζα. Ο Αϊνστάιν συνειδητοποίησε ότι αυτό σήμαινε ότι ένα πείραμα που πραγματοποιείται σ’ ένα επιταχυνόμενο σύστημα αναφοράς δεν θα μπορούσε να διακρίνει τις δυνάμεις που οφείλονται στην επιτάχυνση από εκείνες που οφείλονται στη βαρύτητα. Αυτό τον οδήγησε στο ότι θα πρέπει οι νόμοι της Φυσικής να διέπονται από μια μεγαλύτερη συμμετρία, η οποία περιλαμβάνει και την επιτάχυνση. Συνειδητοποίησε ακόμα ότι η αρχή της ισοδυναμίας υπονοεί ότι ο χωρόχρονος είναι καμπυλωμένος και ότι η δύναμη της βαρύτητας είναι μια άμεση συνέπεια αυτής της καμπύλωσης. H συμμετρία που ανακάλυψε είναι γνωστή ως diffeomorphism invariance και σημαίνει ότι οι νόμοι της Φυσικής έχουν την ίδια μορφή σε οποιοδήποτε τετραδιάστατο σύστημα συντεταγμένων στο χωρόχρονο (Γενική θεωρία της Σχετικότητας). Στη Γενική θεωρία της Σχετικότητας ο χωρόχρονος και η ύλη συγχωνεύονται, παύουν δηλαδή να είναι ξεχωριστές οντότητες, κατ’ αναλογία με την Ειδική θεωρία της Σχετικότητας που ενοποιεί το χώρο και τον χρόνο σε μία οντότητα, το χωρόχρονο.
Στο δεύτερο μισό του εικοστού αιώνα θεμελιώθηκε και αποδείχτηκε πειραματικά με εκπληκτική ακρίβεια η Κβαντική Ηλεκτροδυναμική, η θεωρία που περιγράφει τις ηλεκτρομαγνητικές αλληλεπιδράσεις. Και αυτή η θεωρία είναι άρρηκτα συνδεδεμένη με μια συμμετρία, την τοπική συμμετρία βαθμίδας U(1). Πρόκειται για μια συμμετρία που μοιάζει με τη συμμετρία σε στροφές, όχι όμως στον πραγματικό τρισδιάστατο χώρο, αλλά στον εσωτερικό και αφηρημένο χώρο των κυματοσυναρτήσεων των σωματιδίων. Έτσι ο ηλεκτρομαγνητισμός μπορεί να συνοψιστεί στην ακόλουθη πρόταση: Το σύμπαν μας χαρακτηρίζεται από μια τοπική συμμετρία βαθμίδας U(1). Το διατηρούμενο μέγεθος σ’ αυτή την περίπτωση είναι το ηλεκτρικό φορτίο.
Μια άλλη συμμετρία SU(3) χαρακτηρίζει τις ισχυρές αλληλεπιδράσεις (αλληλεπιδράσεις μεταξύ κουάρκ, αντικουάρκ και γκλουονίων). Πρόκειται και πάλι για συμμετρία σε ένα είδος στροφών, αυτή τη φορά όμως στον εσωτερικό κόσμο των κουάρκς, (τον χώρο των «χρωμάτων» γιατί γνωρίζουμε πως τα κουάρκ έχουν κι έναν άλλο βαθμό ελευθερίας, έναν κβαντικό αριθμό, το χρώμα.) Κάθε κουάρκ μπορεί να έχει τρεις καταστάσεις- χρώματα που συμβολικά τα ονομάζουμε κόκκινο, μπλε, πράσινο. Έχουμε μάλιστα δει ότι όλα τα αδρόνια είναι άχρωμα που σημαίνει ότι τα αδρόνια είναι αναλλοίωτα σε στροφές στο χώρο των «χρωμάτων». Το διατηρούμενο μέγεθος σ’ αυτήν την περίπτωση είναι το «χρώμα». H απαίτηση η θεωρία που περιγράφει τον κόσμο των κουάρκ να είναι αναλλοίωτη κάτω από τοπικούς μετασχηματισμούς στο χώρο των χρωμάτων, οδήγησε στην ανάπτυξη της Κβαντικής Χρωμοδυναμικής, η οποία ορίζει την ύπαρξη οκτώ μποζονίων βαθμίδας (οκτώ γκλουόνια) που είναι οι φορείς ή διαδότες της ισχυρής δύναμης. H δύναμη της συμμετρίας έγκειται στο ότι οδηγεί στην ανάπτυξη μιας ολόκληρης θεωρίας που περιγράφει πώς αλληλεπιδρά η ύλη με το πεδίο.
Μια συμμετρία με ακόμα πιο πολύπλοκο όνομα SU(2)XU(1)γ χαρακτηρίζει και «ενοποιεί» τις ηλεκτρομαγνητικές και ασθενείς αλληλεπιδράσεις, προβλέποντας την ύπαρξη τριών μποζονίων βαθμίδας, τριών πεδίων, επιπλέον του φωτονίου. H μεγάλη διαφορά τους από το γνωστό μας φωτόνιο είναι ότι έχουν μάζα, γεγονός που εξηγεί τη μικρή εμβέλεια των ασθενών αλληλεπιδράσεων. H ύπαρξη αυτών των πεδίων διαπιστώθηκε πειραματικά στα πειράματα U(1) και U(2) το 1983 στο CERN, μια από τις μεγαλύτερες επιτυχίες της φυσικής των τελευταίων δεκαετιών.
Φυσικά υπάρχουν συμμετρίες τις οποίες δεν αναφέραμε. Το θέμα είναι πολύ μεγάλο έτσι ώστε η εκτενής και η εις βάθος παρουσίαση του είναι αδύνατη στα πλαίσια αυτού του άρθρου. Είδαμε όμως, αν και πολύ συνοπτικά, ότι από την εποχή του Αριστοτέλη μέχρι και τις μέρες μας η έννοια της συμμετρίας έπαιξε ολοένα και πιο καθοριστικό, με την πάροδο του χρόνου, ρόλο στην αναζήτηση και στην ανακάλυψη των νόμων της Φυσικής. Είδαμε επίσης ότι η συμμετρία είναι μια ενοποιητική έννοια. Είναι λοιπόν ίσως εύλογο ν’ αναρωτηθεί κανείς αν υπάρχει μια μεγαλύτερη, άγνωστη ακόμα, συμμετρία που χαρακτηρίζει όλες τις δυνάμεις στη φύση. Αυτό είναι ένα από τα μεγάλα ερωτήματα που θέτει και φυσικά καλείται ν’ απαντήσει η μοντέρνα Φυσική.
Το άρθρο αυτό βασίστηκε σε μια ομιλία της Κ. Ζαχαριάδου (ΕΚΕΦΕ Δημόκριτος) που έγινε σε μαθητές
Αναφορές
1. O χαρακτήρας του Φυσικού Νόμου, Richard Feynman
2. H εξέλιξη των ιδεών στη Φυσική, Albert Einstein -Leopold lnfeld
3. H ελαφρότητα της βαρύτητας, Jayant Narlikar
Leave a Comment