Η «θεωρία των πάντων» είναι μία από τα πιο αγαπημένα όνειρα της επιστήμης ή το Ιερό Δισκοπότηρο όλων των φυσικών. Αν βρεθεί ποτέ, θα περιγράφει τη λειτουργία του σύμπαντος στο πιο θεμελιώδες επίπεδο και, επομένως, θα περικλείει όλη την γνώση μας για τη φύση. Θα απαντά, επίσης, σε κάποια διαρκή αινίγματα, όπως τι είναι η σκοτεινή ύλη, η αιτία που ρέει ο χρόνος σε μία μόνο κατεύθυνση και το πώς λειτουργεί η βαρύτητα. Ο Stephen Hawking είπε κάποτε ότι μια τέτοια θεωρία θα είναι "ο τελικός θρίαμβος της ανθρώπινης λογικής – και από τότε θα πρέπει να γνωρίζουμε το μυαλό του Θεού".

Όμως, οι θεολόγοι για καιρό ακόμα δεν θα χάνουν τον ύπνο τους. Παρά τις προσπάθειες δεκαετιών για την ενοποίηση όλων των θεωριών, η πρόοδος ήταν αργή. Αντί για μία ή δύο αντίπαλες θεωρίες οι οποίες βάσιμα μπορεί να αξιολογηθούν βάσει αποδεικτικών στοιχείων, υπάρχουν πολλές υποψήφιες θεωρίες των πάντων, αλλά με λίγες πολύτιμες ενδείξεις για το ποια (αν υπάρχουν) θα μπορούσε να αποδειχθεί σωστή.
Εδώ υπάρχει ένας σύντομος οδηγός για τις έξι θεωρίες:
1.Θεωρία χορδών
Είναι ίσως η πιο γνωστή θεωρία των πάντων, και αυτή που έχει μελετηθεί πιο πολύ. Αφήνει να εννοηθεί ότι τα θεμελιώδη σωματίδια που παρατηρούμε στην πραγματικότητα δεν είναι καθόλου σωματίδια, αλλά μικροσκοπικές χορδές που ανάλογα με τον τρόπο ταλάντωσης τους, παίρνουν τη μορφή των γνωστών σωματιδίων.
 Πάνω: ένας χώρος Calabi-Yau είναι από τις πιο ελπιδοφόρες υποψήφιες θεωρίες για τα πληθωριστικά μοντέλα της θεωρίας χορδών
Πάνω: ένας χώρος Calabi-Yau είναι από τις πιο ελπιδοφόρες υποψήφιες θεωρίες για τα πληθωριστικά μοντέλα της θεωρίας χορδών
Επιπλέον, τα μαθηματικά της θεωρίας χορδών επικαλούνται πρόσθετες χωρικές διαστάσεις, τις οποίες οι άνθρωποι δεν μπορούν να βιώσουν άμεσα. Μπορεί να είναι ριζοσπαστικές προτάσεις, αλλά πολλοί θεωρητικοί βρίσκουν την προσέγγιση των χορδών κομψή, και μάλιστα έχουν προτείνει πολυάριθμες παραλλαγές της βασικής θεωρίας, που φαίνεται να λύνουν κάποια κοσμολογικά αινίγματα. Ωστόσο, έχουν δύο μεγάλες προκλήσεις να ξεπεράσουν εάν θέλουν να πείσουν την υπόλοιπη επιστημονική κοινότητα ότι η θεωρία χορδών είναι η καλύτερη υποψήφια για μια θεωρία των πάντων.
Πρώτον, οι θεωρητικοί των χορδών μέχρι τώρα αγωνίζονται να κάνουν νέες προβλέψεις που μπορούν να ελεγχθούν πειραματικά. Έτσι, η θεωρία χορδών παραμένει ακριβώς αυτό που λέει: μια θεωρία.
Δεύτερον, υπάρχουν πάρα πολλές παραλλαγές της θεωρίας, κάθε μία εκ των οποίων θα μπορούσε να είναι σωστή – που διαφέρουν λίγο μεταξύ τους. Για να λύσουν αυτό το πρόβλημα, μερικοί φυσικοί έχουν προτείνει ένα γενικότερο πλαίσιο που ονομάζεται Μ-θεωρία, η οποία ενοποιεί πολλές θεωρίες χορδών.
Όμως η τελευταία έχει και τα δικά της προβλήματα. Ανάλογα με τον τρόπο που αυτή θα συσταθεί, η Μ-θεωρία μπορεί να περιγράψει οποιαδήποτε από 10500 σύμπαντα. Μερικοί φυσικοί υποστηρίζουν ότι αυτό το τεράστιο νούμερο είναι απόδειξη ότι υπάρχουν πολλαπλά σύμπαντα, αλλά άλλοι πιστεύουν ότι αυτό σημαίνει απλώς ότι η θεωρία δεν είναι ελέγξιμη.
Διαβάστε και τα σχετικά άρθρα:
Το σημερινό τοπίο στη θεωρία χορδών
Θεωρία Χορδών: Είναι το τελευταίο αδιέξοδο της επιστήμης;
Το επόμενο κορυφαίο μοντέλο θα είναι η θεωρία χορδών
2. Κβαντική βαρύτητα βρόχων
Αν και δεν είχε την ίδια προβολή στα μέσα ενημέρωσης, η κβαντική βαρύτητα βρόχων είναι μέχρι στιγμής ο μόνος πραγματικός αντίπαλος της θεωρίας χορδών.
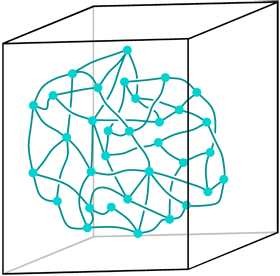 Αριστερά: Ο ιστός του χώρου είναι ένα δίκτυο σπιν με γραμμές και κόμβους (τελείες). Ο μικρότερος όγκος 10-99 εκατοστά αντιστοιχεί σε ένα κόμβο που το φως θέλει χρόνο 10-43 δευτερόλεπτα για να τον διασχίσει. Μεταξύ των κόμβων και πάνω στις γραμμές τοποθετούνται σύμβολα που αναπαριστούν ή τις δυνάμεις της φύσης, όπως πχ η δύναμη της βαρύτητας, ή διάφορα σωματίδια που βρίσκονται εκεί. Η κίνηση σωματιδίων στο χώρο απεικονίζεται με αυτά τα σύμβολα να μετακινούνται με το μικρότερο δυνατό βήμα. Ο κβαντικός χωρόχρονος περιγράφεται από αντίστοιχα διαγράμματα, που ονομάζονται αφροί σπιν.
Αριστερά: Ο ιστός του χώρου είναι ένα δίκτυο σπιν με γραμμές και κόμβους (τελείες). Ο μικρότερος όγκος 10-99 εκατοστά αντιστοιχεί σε ένα κόμβο που το φως θέλει χρόνο 10-43 δευτερόλεπτα για να τον διασχίσει. Μεταξύ των κόμβων και πάνω στις γραμμές τοποθετούνται σύμβολα που αναπαριστούν ή τις δυνάμεις της φύσης, όπως πχ η δύναμη της βαρύτητας, ή διάφορα σωματίδια που βρίσκονται εκεί. Η κίνηση σωματιδίων στο χώρο απεικονίζεται με αυτά τα σύμβολα να μετακινούνται με το μικρότερο δυνατό βήμα. Ο κβαντικός χωρόχρονος περιγράφεται από αντίστοιχα διαγράμματα, που ονομάζονται αφροί σπιν.
Η βασική ιδέα είναι ότι ο χώρος δεν είναι συνεχής, όπως συνηθίζουμε να πιστεύουμε, αλλά είναι διαιρεμένος σε μικροσκοπικά κομμάτια πλάτους 10-35 μέτρα. Αυτά πάλι συνδέονται με δεσμούς για να κάνουν τον χώρο στη συνέχεια να τον αντιλαμβανόμαστε όπως τον ξέρουμε. Όταν αυτοί οι δεσμοί είναι πεπλεγμένοι σε πλεξούδες και κόμβους, παράγουν τα στοιχειώδη σωματίδια.
Η κβαντική βαρύτητα βρόχων έχει κάνει κάποιες δειλές προβλέψεις φαινομένων του πραγματικού κόσμου, και επίσης έχει ρίξει κάποιο φως στη γέννηση του σύμπαντος. Όμως, οι υποστηρικτές της μέχρι τώρα αγωνίζονται για να ενσωματώσουν την βαρύτητα στις θεωρίες τους. Και όπως με τη θεωρία χορδών, μια πραγματική πειραματική δοκιμή (έλεγχος) είναι ακόμα κάπως μακρινή.
Διαβάστε και τα σχετικά άρθρα:
Η κβαντική βαρύτητα βρόχων
Είμαστε φτιαγμένοι από χωρόχρονο λέει η κβαντική βαρύτητα βρόχων
Το Σύμπαν: Ένας Κβαντικός Βρόγχος
3. Αιτιώδης δυναμικός τριγωνισμός ή CDT

Δεξιά: Μικρά πλακίδια φτιάχνουν το Σύμπαν, όπως ακριβώς μπορείτε να κολλήσετε έξι ισόπλευρα τρίγωνα μαζί σε ένα σημείο για να κάνετε ένα τμήμα επίπεδου χώρου, έτσι και η θεωρία CDT μπορεί να παράγει επίπεδο, θετικά ή αρνητικά κυρτωμένο χωρόχρονο. Τα τρίγωνα αυτά δεν είναι φυσικά αντικείμενα. Αντίθετα, είναι ένα μαθηματικό και υπολογιστικό εργαλείο – που οδηγούν σε επιβλητικά αποτελέσματα για το σύμπαν μας.
Ο αιτιώδης δυναμικός τριγωνισμός φαίνεται αρκετά παρόμοια με αυτήν της κβαντικής βαρύτητας βρόχων με μια πρώτη ματιά. Ακριβώς όπως και η κβαντική βαρύτητα βρόχων σπάζει τον χώρο σε μικροσκοπικές «δομικές μονάδες», η CDT υποθέτει ότι ο χωροχρόνος είναι χωρισμένος σε μικρά δομικά στοιχεία – αλλά αυτή τη φορά τα κομμάτια είναι τεσσάρων διαστάσεων που λέγονται πενταχωρόνια (pentachorons).
Τα πενταχωρόνια μπορεί στη συνέχεια να κολλάνε μαζί για την δημιουργία ενός σύμπαντος μεγάλης κλίμακας – που αποδεικνύεται ότι έχει τρεις χωρικές διαστάσεις και μία διάσταση του χρόνου, όπως ακριβώς είναι στην πραγματικότητα και ο Κόσμος μας. Μέχρι στιγμής πάει καλό, αλλά υπάρχει ένα σημαντικό μειονέκτημα: Η CDT ως έχει αυτή τη στιγμή δεν μπορεί να εξηγήσει την ύπαρξη της ύλης.
Διαβάστε και τα:
Αιτιώδης δυναμικός τριγωνισμός: Πρώτος ριζοσπαστικός δρόμος για μια Θεωρία των Πάντων
Πως να κατασκευάσετε το Σύμπαν
4. Κβαντική Βαρύτητα Αϊνστάιν
Αυτή η ιδέα, που προτάθηκε αρχικά από τον Martin Reuter του Πανεπιστημίου του Mainz, παίρνει έναν μάλλον διαφορετικό δρόμο.
Ένας κομμάτι του προβλήματος για την ενοποίηση της βαρύτητας με την κβαντική μηχανική είναι τι συμβαίνει με την βαρύτητα στις μικρές κλίμακες. Όσο πιο κοντά είναι δύο αντικείμενα μεταξύ τους, τόσο ισχυρότερη είναι η βαρυτική έλξη τους. Αλλά η βαρύτητα ενεργεί, επίσης, και στον εαυτό της, και ως εκ τούτου, σε πολύ μικρές αποστάσεις ξεκινά ένας βρόχος ανάδρασης. Σύμφωνα με τις συμβατικές θεωρίες η δύναμη θα πρέπει να γίνει τρομακτικά μεγάλη σε μικροσκοπικές αποστάσεις – που σημαίνει ότι υπάρχει κάτι λάθος με τις συμβατικές θεωρίες.
Ωστόσο, ο Reuter έχει βρει έναν τρόπο για να δημιουργήσει ένα «σταθερό σημείο»: μια απόσταση κάτω από την οποία η βαρύτητα σταματά να γίνεται ολοένα και πιο ισχυρή. Θα μπορούσε λοιπόν αυτή η ιδέα να βοηθήσει στην επίλυση του πιο πάνω προβλήματος, και να οδηγήσει σε μια κβαντική θεωρία της βαρύτητας.
Διαβάστε και το:
Κβαντική Βαρύτητα Αϊνστάιν : Δεύτερος ριζοσπαστικός δρόμος για μια Θεωρία των Πάντων
5. Κβαντικό μοντέλο γραφημάτων
 Όλες οι παραπάνω θεωρίες υποθέτουν ότι υπάρχει τόσο ο χώρος όσο και ο χρόνος, και στη συνέχεια προσπαθούν να δημιουργήσουν το υπόλοιπο σύμπαν. Το κβαντικό μοντέλο γραφημάτων – το πνευματικό τέκνο της Φωτεινής Μαρκοπούλου του Ινστιτούτου Θεωρητικής Φυσικής Perimeter στο Waterloo του Καναδά – προσπαθεί να τα καταργήσει.
Όλες οι παραπάνω θεωρίες υποθέτουν ότι υπάρχει τόσο ο χώρος όσο και ο χρόνος, και στη συνέχεια προσπαθούν να δημιουργήσουν το υπόλοιπο σύμπαν. Το κβαντικό μοντέλο γραφημάτων – το πνευματικό τέκνο της Φωτεινής Μαρκοπούλου του Ινστιτούτου Θεωρητικής Φυσικής Perimeter στο Waterloo του Καναδά – προσπαθεί να τα καταργήσει.
Όταν το σύμπαν δημιουργήθηκε στο big bang, λέει η Μαρκοπούλου, δεν υπήρχε ο χώρος όπως τον ξέρουμε. Αντίθετα, υπήρξε ένα αφηρημένο δίκτυο από «κόμβους» του χώρου, στον οποίο ο κάθε κόμβος συνδέεται με κάθε άλλο. Πολύ σύντομα στη συνέχεια, αυτό το δίκτυο κατέρρευσε και ορισμένοι από τους κόμβους απομακρύνθηκαν μακριά από κάθε άλλο, αποτελώντας το μεγάλο σύμπαν που βλέπουμε σήμερα.
Διαβάστε και το:
Κβαντικό μοντέλο γραφημάτων : Τρίτος ριζοσπαστικός δρόμος για μια Θεωρία των Πάντων
6. Εσωτερική σχετικότητα
Αναπτύχθηκε από τον Olaf Dreyer του MIT (τον σύζυγο της Φωτεινής Μαρκοπούλου), και προσπαθεί να εξηγήσει πώς η γενική σχετικότητα θα μπορούσε να προκύψει σε ένα κβαντικό κόσμο.
Κάθε σωματίδιο στο σύμπαν έχει μια ιδιότητα που λέγεται "σπιν", η οποία μπορεί να θεωρηθεί κάτι σαν την στροφορμή των σωματιδίων όταν περιστρέφονται. Στο μοντέλο του Dreyer υπάρχει ένα σύστημα σπιν που υφίστανται ανεξάρτητα από την ύλη και είναι τοποθετημένα τυχαία. Όταν το σύστημα φθάσει σε μια κρίσιμη θερμοκρασία, τα σπιν ευθυγραμμίζονται και σχηματίζοντας ένα διατεταγμένο μοτίβο.
Όποιος πραγματικά ζει μέσα στο σύστημα των σπιν δεν θα τα δει. Όλοι αυτοί βλέπουν τα αποτελέσματά τους, που όπως έχει δείξει ο Dreyer θα περιλαμβάνει τον χωροχρόνο και την ύλη. Ο ίδιος ο Dreyer έχει, επίσης, καταφέρει να συλλάβει τη νευτώνεια βαρύτητα από το μοντέλο του: ωστόσο, η γενική σχετικότητα δεν έχει ακόμη εμφανιστεί σε αυτό το μοντέλο.
Διαβάστε και το:
Εσωτερική σχετικότητα : Τέταρτος ριζοσπαστικός δρόμος για μια Θεωρία των Πάντων
7. E8
Το 2007 ο φυσικός (και καμιά φορά σέρφερ) Garrett Lisi ανάγκασε τον κόσμο να ασχοληθεί μαζί του, γιατί μια κομψή συμμετρική μαθηματική δομή – η Ε8 – μπορεί τελικά να αποκαλύπτει τον σύνδεσμο ανάμεσα στη βαρύτητα και στις άλλες θεμελιώδεις δυνάμεις της φύσης. Αυτό προτείνει ο Garrett Lisi ένας αιρετικός φυσικός που ξοδεύει περισσότερο χρόνο πάνω στη σανίδα του σερφ παρά μπροστά στις εξισώσεις του.
 Η μαθηματική αυτή δομή βρέθηκε το 1887, αλλά κατανοήθηκε πλήρως από τους μαθηματικούς το 2007 μετά από δουλειά, που αν γραφεί σε μικρά γράμματα, θα μπορούσε να καλύψει μια επιφάνεια στο μέγεθος του Manhattan
Η μαθηματική αυτή δομή βρέθηκε το 1887, αλλά κατανοήθηκε πλήρως από τους μαθηματικούς το 2007 μετά από δουλειά, που αν γραφεί σε μικρά γράμματα, θα μπορούσε να καλύψει μια επιφάνεια στο μέγεθος του Manhattan
Η αναστάτωση αυτή προκλήθηκε από ένα δημοσιευμένο άρθρο όπου συζητούσε το Ε8, ένα σύνθετο μαθηματικό μοντέλο οκτώ διαστάσεων με 248 σημεία. Ο Lisi έδειξε ότι τα διάφορα θεμελιώδη σωματίδια και οι γνωστές δυνάμεις της φυσικής θα μπορούσαν να τοποθετηθούν στα σημεία του μοτίβου Ε8, και ότι πολλές από τις αλληλεπιδράσεις τους, εν συνέχεια προκύπτουν φυσιολογικά.
Μερικοί φυσικοί επέκριναν έντονα την δημοσίευση, ενώ άλλοι το αντιμετώπισαν πιο προσεκτικά. Στα τέλη του 2008, δόθηκε επιχορήγηση στον Lisi για να συνεχίσει τις σπουδές του πάνω στο Ε8.
Δείτε και το σχετικό άρθρο
Είναι ένα μαθηματικό σχήμα η θεωρία του παντός;
Λύθηκε ένα αίνιγμα 248 διαστάσεων (οι αναπαραστάσεις της ομάδας Ε8) Η θεωρία του παντός σε 248 απλά βήματα
Πηγή: New Scientist



Leave a Comment