Στον Ρώσο μαθηματικό Grigoriy Perelman απονεμήθηκε βραβείο του ενός εκατομμυρίου δολαρίων για την επίλυση ενός από πιο δύσκολα προβλήματα στην ιστορία των μαθηματικών. Αλλά το πραγματικό αίνιγμα είναι αν αυτός θα το αποδεχθεί.
Η απομονωμένος από τον πολύ κόσμο Grigoriy Perelman έχει αναγνωριστεί από την Μαθηματική κοινότητα ότι απέδειξε την Εικασία του Poincaré, ένα από τα επτά προβλήματα το οποίο επιλέχτηκε από το Ινστιτούτο Μαθηματικών Clay (CMI) το 2000, ως το σημαντικότερο από τα άλυτα προβλήματα στα μαθηματικά.
Η εικασία, που προτάθηκε από Ανρί Πουανκαρέ το 1904, ασχολείται με τις ιδιότητες των πεδίων σε τρεις διαστάσεις και με τα σχήματα που είναι δυνατόν να έχει το Σύμπαν.
Η εικασία Πουανκαρέ είναι ένα κεντρικό ζήτημα στην τοπολογία, τη μελέτη των γεωμετρικών ιδιοτήτων των αντικειμένων που δεν αλλάζουν όταν τεντώνονται, διαστρεβλώνονται ή συρρικνώνονται.
Η επιφάνεια της Γης περιγράφεται ως δισδιάστατη σφαίρα από την τοπολογία. Εάν κάποιος την περικύκλωνε με ένα λάσο, θα μπορούσε να την αναγκάσει να περιοριστεί σε ένα σημείο. Στην επιφάνεια του ντόνατς, εντούτοις, ένα λάσο που θα περνούσε μέσα από την τρύπα του στο κέντρο, δεν θα μπορούσε να το περιορίσει σε ένα σημείο χωρίς να κοπεί η επιφάνεια.
Για παράδειγμα η Εικασία του Πουανκαρέ καθορίζει ποια στερεά σώματα (ή πολλαπλότητες σε αφηρημένους μαθηματικούς χώρους άνω των τριών διαστάσεων) είναι ισοδύναμα, από τοπολογική άποψη με μια σφαίρα και ποια όχι. Π.χ. ένας κύβος από πλαστελίνη είναι ισοδύναμος με σφαίρα, αφού μπορούμε να τον πλάσουμε σαν σφαίρα, ενώ ένα ντόνατς δεν είναι, γιατί έχει μια τρύπα στη μέση.
Φαντασθείτε ότι έχετε ένα λάστιχο, ένα μήλο και ένα ντόνατς με τρύπα στη μέση. Αν τραβήξετε το λάστιχο και το τοποθετήσετε περιμετρικά γύρω από το μήλο, θα μπορείτε να μετακινήσετε το λάστιχο από τον «Ισημερινό» στον «Πόλο» του μήλου, χωρίς να σκίσετε το λάστιχο και χωρίς να εγκαταλείψετε την επιφάνεια του μήλου. Αν, όμως, το λάστιχο τοποθετηθεί πάνω στην επιφάνεια του ντόνατς, τότε δεν υπάρχει τρόπος να μετακινήσουμε το λάστιχο σε όλη την επιφάνεια του ντόνατς, χωρίς να το σκίσουμε ή το ένα ή το άλλο. Ο Πουανκαρέ υπέθεσε ότι κάτι ανάλογο συμβαίνει και στον τετραδιάστατο χώρο, ενώ σύγχρονοι Μαθηματικοί απέδειξαν ότι κάτι τέτοιο συμβαίνει και σε χώρο περισσότερων των τεσσάρων διαστάσεων.
Ο Perelman δημοσίευσε μια απόδειξη το 2002, αλλά επειδή απογοητεύτηκε με τους μαθηματικούς, αποσύρθηκε από τη μαθηματική κοινότητα. Το 2006 αρνήθηκε να αποδεχθεί το μετάλλιο Fields για το έργο του, ένα βραβείο που συχνά περιγράφεται ως το βραβείο Νόμπελ των μαθηματικών.
Ο πρόεδρος του Ινστιτούτου CMI, James Carlson, περιμένει να δει εάν ο Perelman θα κάνει το ίδιο και για το βραβείο της Χιλιετίας, όπως λέγεται. “Μπορεί να αργήσει λίγο πριν πάρει την απόφασή του”, λέει.
Η εικασία του Πουανκαρέ είναι το μόνο από τα επτά προβλήματα της Χιλιετίας που έχει λυθεί μέχρι σήμερα, και η μοίρα του χρηματικού έπαθλου είναι αβέβαιη, γιατί δεν ξέρουμε εάν ο Πέρελεμαμ το απορρίψει.
Ελαστικοί λουκουμάδες
Για να καταλάβουμε καλύτερα την εικασία του Poincaré και την απόδειξη του Perelman, χρειάζεται να ξέρουμε κάποια πράγματα γύρω από την τοπολογία. Σ’ αυτόν τον κλάδο των μαθηματικών, το ακριβές σχήμα των αντικειμένων δεν έχει μεγάλη σημασία. Φανταζόμαστε τα αντικείμενα σα να αποτελούνται από εύπλαστη ζύμη ή πλαστελίνη, η οποία μπορεί να εκταθεί, να συμπιεστεί και να λυγίσει σε όποιο βαθμό θέλουμε. Γιατί όμως πρέπει να θεωρούμε αντικείμενα ή χώρους φτιαγμένους από φανταστική εύπλαστη ζύμη; Ο λόγος έχει να κάνει με το γεγονός ότι το ακριβές σχήμα ενός αντικειμένου – η απόσταση μεταξύ δύο σημείων – είναι ένα ουσιαστικό ζήτημα της γεωμετρίας του αντικειμένου. Θεωρώντας αντικείμενα από πλαστελίνη, οι τοπολόγοι ανακαλύπτουν ποιες ιδιότητες του αντικειμένου είναι τόσο θεμελιώδεις ώστε να υπάρχουν ανεξάρτητα της γεωμετρικής δομής του. Μελετώντας τοπολογία είναι σα να ανακαλύπτουμε ποιες ανθρώπινες ιδιότητες είναι τόσο γενικές, με τη χρησιμοποίηση ανθρώπινων μορφών από πλαστελίνη οι οποίες μπορούν να πάρουν τη μορφή κάθε ανθρώπου. Οι τοπολόγοι λένε χαρακτηριστικά ότι γι αυτούς ένας λουκουμάς με σχήμα δαχτυλιδιού και ένα φλιτζάνι δεν ξεχωρίζουν. Αυτό σημαίνει ότι μπορούμε να μορφοποιήσουμε ένα φλιτζάνι από πλαστελίνη σε σχήμα λουκουμά, πιέζοντας την πλαστελίνη γύρω-γύρω, χωρίς ν’ ανοίξουμε τρύπες ή να κολλήσουμε ανεξάρτητες περιοχές του.(Βλέπε παρακάτω σχήμα).
Μια μπάλα από την άλλη μεριά, μπορεί να μετατραπεί σε λουκουμά, μόνο αν ανοίξουμε μια τρύπα στο μέσον της ή αν την τεντώσουμε στο ανάπτυγμα ενός κυλίνδρου και κολλήσουμε μαζί τα άκρα του αναπτύγματος αυτού.Επειδή όμως χρειάζονται τέτοια κοψίματα και κολλήματα, μια μπάλα δεν είναι ίδια τοπολογικά με ένα λουκουμά.
Αυτό που ενδιαφέρει περισσότερο τους τοπολόγους είναι η επιφάνεια της μπάλας και του λουκουμά. Έτσι αντί να φανταζόμαστε ένα στερεό σώμα, θα φανταζόμαστε και στις δύο περιπτώσεις την ελαστική επιφάνεια ενός μπαλονιού στο σχήμα που μας ενδιαφέρει. Οι τοπολογίες εξακολουθούν να διαφέρουν: ένα σφαιρικό μπαλόνι δεν μπορεί να μορφοποιηθεί σε ένα δακτυλιοειδές μπαλόνι, το οποίο λέγεται τόρος. Τοπολογικά, μια σφαίρα και ένας τόρος είναι διαφορετικά πράγματα. Οι πρώτοι τοπολόγοι καταπιάστηκαν με το ζήτημα, πόσα διαφορετικά τοπολογικά αντικείμενα υπάρχουν και πως θα μπορούσαν αυτά να χαρακτηριστούν. Για τα 2-διάστατα αντικείμενα, τα οποία λέγονται επίσης και επιφάνειες, η απάντηση είναι καθαρή: Ο αριθμός τους εξαρτάται από το πόσα "χερούλια" δηλαδή λαβές έχουν.
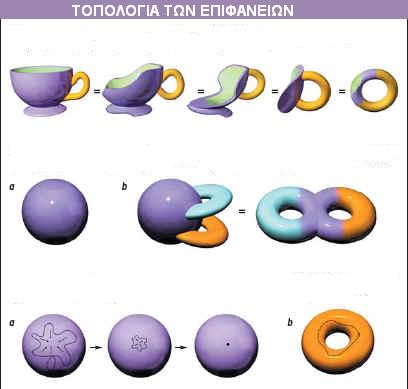
Πρώτη σειρά: Στην τοπολογία, το ακριβές σχήμα δηλαδή η γεωμετρία δεν είναι κάτι σημαντικό. Είναι σαν να είναι όλα κατασκευασμένα από πλαστελίνη ή λάστιχο και να μπορούμε να τα διαμορφώνουμε με έκταση, συμπίεση ή συστροφή. Απαγορεύεται ωστόσο να τα κόψουμε ή να τα κολλήσουμε. Έτσι στην τοπολογία, κάθε αντικείμενο με μια μόνο τρύπα, όπως στο φλιτζάνι του καφέ (άνω εικόνα, αριστερά), είναι ισοδύναμο με τον λουκουμά, στα δεξιά.
Δεύτερη σειρά: Κάθε πιθανή 2-διάστατη πολλαπλότητα, ή επιφάνεια, – αν περιοριστούμε στις συμπαγείς και προσανατολισμένες – μπορεί να κατασκευαστεί αν πάρουμε μια σφαίρα (ένα μπαλόνι), και του προσθέσουμε λαβές. Η πρόσθεση μιας λαβής μας δίνει μια επιφάνεια τύπου-1, δηλαδή ένα τόρο, που είναι η επιφάνεια του λουκουμά (επάνω δεξιά). Προσθέτοντας δύο λαβές παίρνουμε την επιφάνεια τύπου-2 [b] κοκ.
Τρίτη σειρά: Η 2-σφαίρα είναι μοναδική μεταξύ των επιφανειών, κατά το ότι οποιοσδήποτε κλειστός βρόχος, εμφυτευμένος πάνω σε μια 2-σφαίρα μπορεί να συρρικνωθεί σε ένα σημείο [α].Αντίθετα, ένας βρόχος πάνω σε ένα τόρο, μπορεί να παγιδευτεί γύρω από την τρύπα στο μέσον [b]. κάθε επιφάνεια εκτός από την 2-σφαίρα, έχει λαβές πάνω στις οποίες μπορεί να παγιδευτεί ο βρόχος. Η εικασία του Poincaré προτείνει ότι η 3-σφαίρα είναι μοναδική μεταξύ των 3-διάστατων πολλαπλοτήτων. Κάθε βρόχος πάνω σ’ αυτήν μπορεί να συρρικνωθεί σε ένα σημείο, αλλά ο βρόχος πάνω σε οποιαδήποτε άλλη πολλαπλότητα μπορεί να παγιδευτεί.
Κατά το τέλος του 19ου αιώνα, οι μαθηματικοί κατάλαβαν πως να ταξινομήσουν τις επιφάνειες. Από όλες τις επιφάνειες, η γνωστή μας σφαίρα είχε μια μοναδική απλότητα. Φυσικά στη συνέχεια στράφηκαν στις 3-διάστατες πολλαπλότητες.Το πρώτο ερώτημα που έθεσαν ήταν αν η 3-σφαίρα ήταν μοναδική σε απλότητα, ανάλογη με την 2-σφαίρα. Η πορεία ενός αιώνα που ακολούθησε, ήταν γεμάτη λανθασμένα βήματα και λανθασμένες αποδείξεις.
Ο Henri Poincaré αντιμετώπισε άμεσα αυτό το πρόβλημα. Ήταν ένας εκ των δύο επιφανέστερων μαθηματικών στο κατώφλι του 20ου αιώνα. Ο άλλος ήταν ο David Hilbert. Ο Poincaré ήταν ίσως ο τελευταίος "ολιστής" μαθηματικός. Καταπιανόταν με όλους τους κλάδους των μαθηματικών. Τόσο με τα καθαρά μαθηματικά όσο και με τα εφαρμοσμένα. Είχε συνεισφορά επίσης στις θεωρίες της ουράνιας μηχανικής, στον ηλεκτρομαγνητισμό και στη φιλοσοφία της επιστήμης όπου έγραψε μερικά αρκετά δημοφιλή εκλαϊκευμένα βιβλία.
Ο Poincaré δημιούργησε τον κλάδο των μαθηματικών που ονομάστηκε αλγεβρική τοπολογία. Γύρω στα 1900, χρησιμοποιώντας τεχνικές από το πεδίο αυτό, δημιούργησε ένα μέτρο της τοπολογίας των αντικειμένων που αποκλήθηκε ομοτοπία. Για να καθορίσουμε την ομοτοπία μιας πολλαπλότητας, ας φανταστούμε ότι εμφυτεύουμε ένα κλειστό βρόχο μέσα στην πολλαπλότητα (βλέπε τελευταία σειρά της επάνω εικόνας). Ο βρόχος μπορεί να τυλιχτεί γύρω από την πολλαπλότητα με κάθε δυνατό τρόπο. Θέτουμε λοιπόν την ερώτηση: μπορεί ο βρόχος να συρρικνωθεί σε ένα σημείο πάντοτε, μετακινώντας τον απλώς πάνω στην πολλαπλότητα, χωρίς να έχουμε το δικαίωμα να σηκώσουμε κάποιο τμήμα του από την πολλαπλότητα; Σε ένα τόρο η απάντηση είναι όχι. Αν ο βρόχος διατρέχει την περιφέρεια του τόρου, δεν μπορεί να συρρικνωθεί σε ένα σημείο και παγιδεύεται στον εσωτερικό δακτύλιο του λουκουμά. Η ομοτοπία λοιπόν είναι ένα μέτρο, όλων των διαφορετικών τρόπων που μπορεί να παγιδευτεί ο βρόχος.
Σε μια n-σφαίρα, αδιάφορο πόσο μπλεγμένος μπορεί να είναι αρχικά ο βρόχος, πάντα μπορεί να ξεμπερδευτεί και να συρρικνωθεί σ’ ένα σημείο. Σημειωτέον ότι επιτρέπεται να περάσει ο βρόχος μέσα από τον εαυτό του, κατά τη διάρκεια αυτών των χειρισμών. Ο Poincaré έκανε την εικασία ότι η μόνη 3-πολλαπλότητα επί της οποίας κάθε δυνατός βρόχος μπορεί να συρρικνωθεί σε ένα σημείο, ήταν η 3-σφαίρα, δεν μπόρεσε όμως να το αποδείξει.
Κατά τις δεκαετίες που ακολούθησαν, πολλοί άνθρωποι ανήγγειλαν ότι απέδειξαν την εικασία, αλλά στην πορεία αποδείχτηκε ότι είχαν κάνει λάθη.
Δείτε και τα σχετικά άρθρα
Η λύση από τον Πέρελεμαν της Εικασίας του Πουανκαρέ το σημαντικότερο επίτευγμα κατά το 2006 σύμφωνα με το Science
Άλυτα μαθηματικά προβλήματα
Leave a Comment