Μια εξίσωση σταρ: E = mc2

H E = mc² είναι η πιο φημισμένη εξίσωση όλων των εποχών. Έχει μπει στο εξώφυλλο του περιοδικού Time. Έχει γίνει το αντικείμενο μιας «βιογραφίας» που χειρίζεται την εξίσωση σαν να ήταν άνθρωπος. Είναι ο τίτλος ενός θεατρικού έργου της Χάλι Φλάναγκαν. Ο  Δαλάι Λάμα έχει δηλώσει ότι είναι «η μοναδική επιστημονική εξίσωση που γνωρίζω». Έχουν γραφτεί γι’ αυτήν ποιήματα και τραγούδια.

Όσοι είναι μιας κάποιας ηλικίας μπορεί να θυμούνται την επιτυχία, «Einstein A Go-Go», από τους Landscape, το συγκρότημα ηλεκτρονικής ποπ της δεκαετίας του 1980, οι στίχοι του οποίου έλεγαν, «You’d better watch out, you’d better beware, coz Albert says that E equals mc squared» («Καλά θα κάνεις να προσέξεις, καλά θα κάνεις να ‘χεις το νου σου, γιατί ο Άλμπερτ λέει ότι το E ισούται με εμ-σι στο τετράγωνο»).

Πιο πρόσφατα, η τραγουδίστρια Μαράια Κάρεϊ έβγαλε ένα άλμπουμ με τίτλο E = MC² , με το δεξιό μέλος της εξίσωσης να παραπέμπει στα αρχικά του ονόματος της. Στη διάρκεια των λεγόμενων επιστημονικών πολέμων της δεκαετίας του 1990, είχε ξεσπάσει διαμάχη με τη θέση της Γαλλίδας φεμινίστριας φιλοσόφου Λυς Ιριγκαρέ, ότι η εξίσωση E = mc²  είναι «σεξιστική εξίσωση», επειδή δίνει προνομιούχα θέση στην ταχύτητα του φωτός.

H εξίσωση έχει εμφανιστεί επίσης σε γραμματόσημα διάφορων χωρών, σε κινηματογραφικές ταινίες (Ένα Σχολείο Πολύ Ροκ), δημοφιλή μυθιστορήματα με επιστημονικές φιλοδοξίες (το Άγγελοι & Δαίμονες του Νταν Μπράουν), και σε πολλά καρτούν και βιντεοπαιχνίδια.

Όλα αυτά μπορεί να μας κάνουν να αναρωτηθούμε, μήπως η E = mc²  δεν είναι πραγματική εξίσωση, αλλά μάλλον μια διασημότητα. Διασημότητα είναι κάποιος, την ύπαρξη του οποίου γνωρίζουν όλοι, χωρίς όμως να ξέρουν πολλά πράγματα για αυτόν. Με τον ίδιο τρόπο, όλοι αναγνωρίζουν αυτήν την εξίσωση, και είναι σίγουροι για τη σπουδαιότητα της, αλλά δεν ξέρουν ποτέ γιατί ακριβώς είναι τόσο σημαντική.

Ξέρουμε πολλά κουτσομπολιά γι’ αυτήν, αλλά και πάλι νιώθουμε πάντα ότι τη βλέπουμε «απ’ έξω». Αναρωτιόμαστε, τι πραγματικά σημαίνει. H προβολή της E = mc² , όπως και η προβολή μιας διασημότητας, μοιάζει να έχει παρασκευαστεί από κάποια μυστηριώδη κοινωνική διεργασία.

O Γάλλος διανοούμενος Ρολάν Μπαρτ έγραψε κάποτε ένα δοκίμιο για τον Αϊνστάιν στο οποίο επεσήμαινε ότι, ενώ οι φωτογραφίες του Αϊνστάιν συχνά τον δείχνουν δίπλα σε έναν πίνακα γεμάτο από ακατανόητα σύμβολα και εξισώσεις, τα καρτούν συχνά τον απεικονίζουν με την κιμωλία στο χέρι δίπλα σε έναν καθαρό πίνακα στον οποίο είναι γραμμένος μόνο αυτός ο συγκεκριμένος τύπος, σαν να του ήλθε έτσι εντελώς ξαφνικά. O Μπαρτ παρατηρεί ότι ο συμβολικός χαρακτήρας αυτής της εξίσωσης αποκαθιστά την εικόνα της «γνώσης που έχει αναχθεί σε έναν τύπο… της επιστήμης που εμπεριέχεται ολοκληρωτικά σε μερικά γράμματα».

Και ο ίδιος ο Αϊνστάιν άρχισε να χρησιμοποιεί αυτήν την εξίσωση στη φημισμένη πλέον, απλοποιημένη της μορφή. Τον Απρίλιο του 1946 κυκλοφόρησε το πρώτο τεύχος του δημοφιλούς πλέον περιοδικού Science Illustrated με ένα άρθρο γραμμένο από τον Αϊνστάιν που είχε τίτλο «E = mc²».

Τ ην 1η Ιουλίου 1946, λιγότερο από ένα χρόνο μετά τις εκρήξεις στη Χιροσίμα και το Ναγκασάκι, και λίγο πριν κλείσουν 41 χρόνια μετά την πρώτη της εμφάνιση στην αρχική μορφή της, η εξίσωση E = mc² εμφανίστηκε στο εξώφυλλο του περιοδικού Time. Το τεύχος συνέπιπτε με μια ατομική δοκιμή στο Νότιο Ειρηνικό. To εξώφυλλο είχε ένα πορτρέτο του ασπρομάλλη πλέον, 66χρονου Αϊνστάιν, τον οποίο περιέγραφε ως έναν «ντροπαλό, σχεδόν άγιο, παιδιάστικο άνθρωπο», δίπλα σε ένα τρομερό σύννεφο-μανιτάρι που υψώνεται πάνω από πολεμικά πλοία. Οι κόκκινες φλόγες στη βάση γίνονται πορτοκαλί και μοβ εκεί που υψώνεται η στήλη του καπνού, καταλήγοντας στο γκρίζο κεφάλι του μανιταριού, πάνω στο οποίο είναι γραμμένη η διαβόητη πλέον εξίσωση: E = mc². H εξίσωση είχε γίνει μια διασημότητα. 

Η γέννηση της εξίσωσης

Όπως τελικά οι διασημότητες δεν είναι παρά άνθρωποι έτσι με τον ίδιο τρόπο η E = mc²  είναι και αυτή μία ακόμη εξίσωση. Όπως συμβαίνει και με άλλες εξισώσεις, η E = mc² δημιουργήθηκε από τη δυσαρέσκεια για τις υπάρχουσες θεωρίες, αρχικά εμφανίστηκε με διαφορετική μορφή από αυτή με την οποία τη γνωρίζουμε σήμερα, αναδιαμόρφωσε τον τρόπο που βλέπουμε τον κόσμο, και είχε απρόσμενες συνέπειες.

Η Ειδική Θεωρία της Σχετικότητας δημοσιεύθηκε στις 26 Σεπτεμβρίου του 1905 και εισήγαγε μερικές ριζικές αλλαγές στις έννοιες του χώρου και του χρόνου. Όμως, ο Αϊνστάιν γρήγορα κατάλαβε ότι μέσα σε αυτή τη θεωρία υπήρχαν περισσότερες συνέπειες από αυτές που θα μπορούσε να προβλέψει ο ίδιος όσο την έγραφε. Μία από τις συνέπειες τη συνειδητοποίησε σχεδόν αμέσως.

Λίγο αργότερα έγραφε στον φίλο του Conrad Habicht:

“Μια συνέπεια της μελέτης πάνω στην ηλεκτροδυναμική όντως μου πέρασε από το νου. Συγκεκριμένα, η αρχή της σχετικότητας, σε συνδυασμό με τις θεμελιώδεις εξισώσεις του Μάξγουελ, απαιτεί η μάζα να είναι άμεσο μέτρο της ενέργειας που εμπεριέχεται σε ένα σώμα. Το φως μεταφέρει και μάζα. Μια αισθητή μείωση της μάζας θα πρέπει να συμβαίνει στην περίπτωση του ραδίου. Το συμπέρασμα είναι διασκεδαστικό και δελεαστικό, μπορεί όμως κάλλιστα ο Παντοδύναμος Θεός να γελά με το όλο θέμα και απλώς να με τραβά από τη μύτη.”

Μια μέρα, αφού δημοσιεύθηκε το άρθρο του για τη σχετικότητα, ο Αϊνστάιν ταχυδρόμησε στο περιοδικό Annalen ένα τρισέλιδο άρθρο που περιέγραφε αυτό το πόρισμα, και είχε τίτλο: «Εξαρτάται η Αδράνεια ενός Σώματος από το Ενεργειακό του Περιεχόμενο;».

Το άρθρο δημοσιεύθηκε αργότερα εκείνο το χρόνο. Όπως επεσήμανε, μεταξύ άλλων, ο ιστορικός της επιστήμης John Rigden, αυτό το άρθρο δεν ανοίγει νέους δρόμους, απλώς επισημαίνει ένα συμπέρασμα που προκύπτει λογικά από το προηγούμενο άρθρο, και που θα μπορούσε εύκολα να είχε αναπτυχθεί σε ένα τελικό τμήμα του.

O Αϊνστάιν ανοίγει το άρθρο του «Ενεργειακού Περιεχομένου» με έναν αφοπλιστικά σεμνό τρόπο. «Τα αποτελέσματα μιας ηλεκτροδυναμικής διερεύνησης που δημοσιεύθηκε από τον γράφοντα πρόσφατα σε αυτό το περιοδικό οδηγούν σε ένα πολύ ενδιαφέρον συμπέρασμα».

Καταλήγει σε αυτό το συμπέρασμα από το παρακάτω παράδειγμα. Ας υποθέσουμε ότι ένα σώμα (ένα άτομο, για παράδειγμα) με μάζα m που ηρεμεί στο σύστημα αναφοράς A εκπέμπει δύο φωτεινές δέσμες προς αντίθετες κατευθύνσεις, καταναλώνοντας επομένως ενέργεια. Ας πούμε ότι η συνολική ποσότητα ενέργειας που χάνεται είναι L (όπως και στο προηγούμενο άρθρο, ο Αϊνστάιν χρησιμοποιεί τα ασυνήθιστα για τα σημερινά δεδομένα σύμβολα L για την ενέργεια και V για την ταχύτητα του φωτός).

Έτσι, κάθε φωτεινή δέσμη μεταφέρει ενέργεια L/2. Ένας παρατηρητής στο A βλέπει το σώμα να μην εμφανίζει συνολική αλλαγή της κινητικής του ενέργειας. Το άτομο παραμένει ακίνητο, έχει αποβάλει ένα μέρος της ενέργειας που είχε ενώ βρισκόταν σε κατάσταση διέγερσης, και συνεχίζει να έχει την ίδια μάζα που είχε αρχικά.

Όμως, ένας παρατηρητής στο B, για τον οποίο το A κινείται, βλέπει κάτι διαφορετικό. H φωτεινή δέσμη που κινείται προς τα εμπρός έχει περισσότερη ορμή από εκείνη που κινείται προς τα πίσω, που σημαίνει ότι το άτομο έχει μια συνολική αλλαγή (μείωση) της κινητικής του ενέργειας. Αυτό μπορεί να συμβεί μόνο αν μειωθεί η ταχύτητα ή η μάζα του ατόμου. Όμως, η ταχύτητα του είναι η ίδια. Στο σύστημα αναφοράς στο οποίο ηρεμεί δεν υπάρχει αλλαγή στην κινητική του κατάσταση. H μόνη άλλη δυνατότητα είναι ότι, από την άποψη του συστήματος αναφοράς στο οποίο το άτομο κινείται, η μάζα του έχει μειωθεί.

H μάζα τού ατόμου δεν έχει αυξηθεί από την άποψη του συστήματος αναφοράς στο οποίο ηρεμεί. H «αδρανειακή του μάζα» είναι η ίδια. Όμως, η μάζα από την άποψη του εργαστηρίου, το οποίο το βλέπει ως ένα κινούμενο σώμα, έχει αλλάξει. Κατά πόσο όμως; Χρησιμοποιώντας τα εργαλεία του προηγούμενου άρθρου του, ο Αϊνστάιν βρίσκει ότι ο συντελεστής μετατροπής είναι και πάλι το β.

O Αϊνστάιν -χρησιμοποιώντας ξανά τα σύμβολα L για την ενέργεια και V για την ταχύτητα του φωτός- συνεχίζει ως εξής:

Αν ένα σώμα εκλύει ενέργεια L με τη μορφή ακτινοβολίας, η μάζα του μειώνεται κατά L/V2. Αφού προφανώς εδώ δεν έχει σημασία αν η ενέργεια που αφαιρείται από το σώμα συμβαίνει να μετατραπεί σε ενέργεια ακτινοβολίας ή σε κάποιο άλλο είδος ενέργειας, οδηγούμαστε στο πιο γενικό συμπέρασμα: η μάζα ενός σώματος είναι ένα μέτρο του ενεργειακού του περιεχομένου.

Αυτή είναι η πρώτη φορά που εμφανίζεται τυπωμένη η ιδέα που τελικά θα γίνει διάσημη ως E = mc². Δεν παρουσιάζεται ρητά με τη μορφή εξίσωσης, και δεν υπάρχουν αυτά τα γνωστά σύμβολα. Όμως διατυπώνεται πλήρως η απρόσμενη, ή και επαναστατική ακόμη, έννοια της μάζας-ενέργειας. Αυτή η έννοια μεταμόρφωσε μερικές από τις πιο θεμελιώδεις ιδέες μας για τον τρόπο που είναι συγκροτημένο το σύμπαν.

Ένωσε δύο πράγματα που πιστεύαμε πάντα ότι είναι τελείως διαφορετικά: την ενέργεια, η αρχή διατήρησης της οποίας ήταν ένα κορυφαίο επίτευγμα της φυσικής του δέκατου ένατου αιώνα, και τη μάζα, η αρχή διατήρησης της οποίας ήταν ένα κορυφαίο επίτευγμα του δέκατου όγδοου αιώνα. Τα δύο αυτά μεγέθη μπορούν να μετατραπούν το ένα στο άλλο.

Αυτή η ιδέα έφερε επίσης επανάσταση στις προϋποθέσεις αντικειμενικότητας. Στη νευτώνεια σκηνή, η ενέργεια και η μάζα παραμένουν ίδιες όταν παρατηρούνται από διαφορετικά αδρανειακά συστήματα αναφοράς. Στη σκηνή τού Αϊνστάιν, παραμένουν ουσιαστικά ίδιες σε χαμηλές ταχύτητας, αλλά αλλάζουν όσο η ταχύτητα του συστήματος αναφοράς πλησιάζει την ταχύτητα του φωτός. Αυτό που είναι αντικειμενικό -αυτό που υπάρχει πραγματικά- είναι οι αλλαγές μήκους και χρόνου κατά τη συγκεκριμένη ποσότητα που παρατηρούνται από ένα άλλο σύστημα αναφοράς με αρκετά μεγάλη ταχύτητα.

Μέσα στα επόμενα χρόνια, ο Αϊνστάιν αναφέρθηκε σε αυτό το αποτέλεσμα αρκετές φορές, αν και πάλι με τη μορφή περιγραφών ή με τα αρχικά του σύμβολα, και όχι ακόμη με τη φημισμένη σημερινή μορφή. Για παράδειγμα, σε μια υποσημείωση σε ένα άρθρο του το 1906, έγραψε ότι «η αρχή της σταθερότητας της μάζας είναι μια ειδική περίπτωση της αρχής της ενέργειας».

Στις αρχές του 1907, σε ένα άλλο άρθρο στο Annalen, αναφέρεται στην ενέργεια, με το σύμβολο ε, στη μάζα, με το ελληνικό γράμμα μ, και στην ταχύτητα του φωτός, με το γράμμα V, και χρησιμοποιεί την εξίσωση  Εδώ, η φημισμένη εξίσωση -η ενέργεια ισούται με τη μάζα επί την ταχύτητα του φωτός στο τετράγωνο- εμφανίζεται με το διορθωτικό παράγοντα β, που καλύπτει την περίπτωση να κινείται το σώμα. Δηλαδή, ας πάρουμε ένα κομμάτι ύλης, π.χ. ένα ηλεκτρόνιο. Σε ηρεμία, κάθε ηλεκτρόνιο έχει την ίδια μάζα. Είναι λες και η φύση έδωσε αυτή τη μάζα σε κάθε ηλεκτρόνιο όταν δημιουργήθηκε. Κάθε φορά που ζυγίζουμε το ηλεκτρόνιο στο δικό του σύστημα αναφοράς, έχει πάντα αυτή τη μάζα.

Τ ώρα, ας υποθέσουμε ότι το κοιτάζουμε από ένα άλλο σύστημα αναφοράς, στο οποίο το ηλεκτρόνιο κινείται. Αν E = mc², και το c είναι σταθερό, τότε το m και το e πρέπει να μεταβάλλονται ακριβώς με τον ίδιο τρόπο καθώς αυξάνεται η ενέργεια. H αδρανειακή μάζα του ηλεκτρονίου – η μάζα του στο δικό του σύστημα αναφοράς – δεν αλλάζει. Όμως η μάζα που μετράς στο εργαστήριο, όπου το βλέπεις να κινείται, αλλάζει. Και το β, ο συντελεστής μετατροπής, είναι ο μετασχηματισμός που σου λέει με τι πρέπει να πολλαπλασιάσεις για να βρεις τη μάζα ηρεμίας. Αν παραλείψουμε αυτόν το διορθωτικό παράγοντα, παίρνουμε αυτό που Αϊνστάιν ονομάζει σε μια υποσημείωση, «τον απλοποιημένο τύπο

μν² = ε₀

Αργότερα εκείνη τη χρονιά, ο Αϊνστάιν άλλαξε τα σύμβολα του και άρχισε να χρησιμοποιεί το c αντί για το V για την ταχύτητα του φωτός. H θεωρία της σχετικότητας περιέχει ένα αποτέλεσμα «εξαιρετικής θεωρητικής σημασίας», λέει. «Η αδρανειακή μάζα και η ενέργεια ενός φυσικού συστήματος εμφανίζονται να είναι πράγματα του ίδιου είδους. Σε σχέση με την αδράνεια, μια μάζα μ είναι ισοδύναμη με ένα ενεργειακό περιεχόμενο μεγέθους μc^{2 »}

Μέσα στα επόμενα λίγα χρόνια, ο Αϊνστάιν ανέπτυξε πληρέστερα την αρχής ισοδυναμίας μάζας-ενέργειας και τις συνέπειες της. Και σε ένα χειρόγραφο για τη θεωρία της σχετικότητας το 1912, στην αρχή μιας συζήτησης του θέματος, γράφει τον παραπάνω τύπο χρησιμοποιώντας το m στη θέση του μ, και το L (όπως και στην πρώτη εκδοχή της εξίσωσης) στη θέση ε, το οποίο όμως μετά διαγράφει, και το γράφει E. Από τότε συνεχίζει να χρησιμοποιεί το E και το c, και τώρα έχουμε τη γνωστή εξίσωση μαζί με το διορθωτικό παράγοντα

 
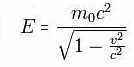
Πηγή: 10 εξισώσεις που άλλαξαν τον Κόσμο του Robert Crease