 Τα μαθηματικά είναι παντού γύρω μας και διαμορφώνουν την κατανόηση που έχουμε για το Κόσμο με αμέτρητους τρόπους.
Τα μαθηματικά είναι παντού γύρω μας και διαμορφώνουν την κατανόηση που έχουμε για το Κόσμο με αμέτρητους τρόπους.
Το 2013, ο μαθηματικός και συγγραφέας της επιστήμης Ian Stewart (αριστερά) δημοσίευσε ένα βιβλίο για 17 υπέροχες εξισώσεις που άλλαξαν τα μαθηματικά αλλά και την ιστορία του κόσμου.
Στο άρθρο αυτό ο Larry Phillips συνοψίζει τις εξισώσεις αυτές και μας επεξηγεί την κάθε μία.
 1) Το Πυθαγόρειο Θεώρημα (530 π.Χ.): Το θεώρημα αυτό είναι θεμελιώδες για την κατανόηση της γεωμετρίας. Περιγράφει τη σχέση μεταξύ των πλευρών ενός ορθογωνίου τριγώνου σε μια επίπεδη επιφάνεια: αθροίζοντας τα τετράγωνα των μικρών πλευρών, a και b, μπορείτε έτσι να πάρετε το τετράγωνο του μήκους της μεγάλης πλευράς, c.
1) Το Πυθαγόρειο Θεώρημα (530 π.Χ.): Το θεώρημα αυτό είναι θεμελιώδες για την κατανόηση της γεωμετρίας. Περιγράφει τη σχέση μεταξύ των πλευρών ενός ορθογωνίου τριγώνου σε μια επίπεδη επιφάνεια: αθροίζοντας τα τετράγωνα των μικρών πλευρών, a και b, μπορείτε έτσι να πάρετε το τετράγωνο του μήκους της μεγάλης πλευράς, c.
Η σχέση αυτή, κατά κάποιο τρόπο, στην πραγματικότητα διακρίνει την κανονική, επίπεδη, Ευκλείδεια γεωμετρία από την κυρτή, μη Ευκλείδεια γεωμετρία. Για παράδειγμα, ένα ορθογώνιο τρίγωνο στην επιφάνεια μιας σφαίρας δεν χρειάζεται να ακολουθεί το Πυθαγόρειο θεώρημα.
 2) Οι λογάριθμοι (John Napier 1610): Οι λογάριθμοι είναι τα αντίστροφα της εκθετικής συνάρτησης. Ένας λογάριθμος σε μια συγκεκριμένη βάση μας λέει σε ποιά δύναμη χρειάζεται να υψώσετε την βάση για να πάρετε έναν αριθμό. Για παράδειγμα, με βάση το 10, ο λογάριθμος του 1 είναι log (1) = 0, αφού 1 = 100, ο log(10) = 1, επειδή 10 = 101 και log (100) = 2, δεδομένου ότι 100 = 102.
2) Οι λογάριθμοι (John Napier 1610): Οι λογάριθμοι είναι τα αντίστροφα της εκθετικής συνάρτησης. Ένας λογάριθμος σε μια συγκεκριμένη βάση μας λέει σε ποιά δύναμη χρειάζεται να υψώσετε την βάση για να πάρετε έναν αριθμό. Για παράδειγμα, με βάση το 10, ο λογάριθμος του 1 είναι log (1) = 0, αφού 1 = 100, ο log(10) = 1, επειδή 10 = 101 και log (100) = 2, δεδομένου ότι 100 = 102.
Η παραπάνω εξίσωση δίπλα παριστάνει το λογάριθμο του γινομένου 2 αριθμών log (ab) = log (α) + log (β), και είναι μία από τις πιο χρήσιμες εφαρμογές των λογαρίθμων: μετατρέπει τον πολλαπλασιασμό σε πρόσθεση.
Μέχρι την ανάπτυξη του ψηφιακού υπολογιστή, αυτός ήταν ο πιο συνηθισμένος τρόπος για να πολλαπλασιάσετε γρήγορα μεγάλους αριθμούς, επιταχύνοντας σε μεγάλο βαθμό τους υπολογισμούς στη φυσική, την αστρονομία και τη μηχανική.
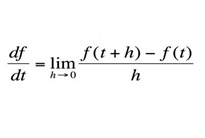 3) Λογισμός (Newton 1668): Ο τύπος που δίνεται εδώ είναι ο ορισμός της παραγώγου στο λογισμό. Η παράγωγος μετρά τον ρυθμό που μία ποσότητα μεταβάλλεται. Για παράδειγμα, μπορούμε να σκεφτούμε την ταχύτητα, σαν την παράγωγο της θέσης – αν περπατάτε με τα πόδια με 5 km την ώρα, στη συνέχεια, κάθε ώρα, έχετε αλλάξετε τη θέση σας κατά 5 km.
3) Λογισμός (Newton 1668): Ο τύπος που δίνεται εδώ είναι ο ορισμός της παραγώγου στο λογισμό. Η παράγωγος μετρά τον ρυθμό που μία ποσότητα μεταβάλλεται. Για παράδειγμα, μπορούμε να σκεφτούμε την ταχύτητα, σαν την παράγωγο της θέσης – αν περπατάτε με τα πόδια με 5 km την ώρα, στη συνέχεια, κάθε ώρα, έχετε αλλάξετε τη θέση σας κατά 5 km.
Φυσικά, ένα μεγάλο μέρος της επιστήμης ενδιαφέρεται για την κατανόηση του πώς τα πράγματα αλλάζουν, και η παράγωγος όπως και το ολοκλήρωμα – το άλλο θεμέλιο του λογισμού – βρίσκονται στην καρδιά του τρόπου που οι μαθηματικοί και οι επιστήμονες κατανοούν την μεταβολή.
 4) Νόμος της βαρύτητας (Newton 1667): ο νόμος της βαρύτητας του Νεύτωνα περιγράφει τη δύναμη F της βαρύτητας μεταξύ δύο αντικειμένων. Η δύναμη αυτή είναι ανάλογη μιας καθολικής σταθεράς, G, των μαζών των δύο αντικειμένων, m1 και m2 και εξαρτάται από την απόσταση μεταξύ των αντικειμένων, r. Ο νόμος του Νεύτωνα είναι ένα αξιόλογο κομμάτι της επιστημονικής ιστορίας – εξηγεί, σχεδόν τέλεια, γιατί οι πλανήτες κινούνται ελλειπτικά. Επίσης, αξιοσημείωτο είναι ο καθολικός χαρακτήρας της – και αυτό σημαίνει ότι η βαρύτητα στη Γη, ή στο ηλιακό μας σύστημα, λειτουργεί το ίδιο οπουδήποτε στο σύμπαν.
4) Νόμος της βαρύτητας (Newton 1667): ο νόμος της βαρύτητας του Νεύτωνα περιγράφει τη δύναμη F της βαρύτητας μεταξύ δύο αντικειμένων. Η δύναμη αυτή είναι ανάλογη μιας καθολικής σταθεράς, G, των μαζών των δύο αντικειμένων, m1 και m2 και εξαρτάται από την απόσταση μεταξύ των αντικειμένων, r. Ο νόμος του Νεύτωνα είναι ένα αξιόλογο κομμάτι της επιστημονικής ιστορίας – εξηγεί, σχεδόν τέλεια, γιατί οι πλανήτες κινούνται ελλειπτικά. Επίσης, αξιοσημείωτο είναι ο καθολικός χαρακτήρας της – και αυτό σημαίνει ότι η βαρύτητα στη Γη, ή στο ηλιακό μας σύστημα, λειτουργεί το ίδιο οπουδήποτε στο σύμπαν.
Την βαρύτητα του Νεύτωνα την κατέχουμε πολύ καλά εδώ και διακόσια χρόνια, ενώ έδωσε τη θέση της στη γενική σχετικότητα του Αϊνστάιν.
 5) Η τετραγωνική ρίζα του –1 (Euler 1750): Οι μαθηματικοί ανέκαθεν ερωτούσαν ποιός πραγματικά να είναι αυτός ο αριθμός, μεταβαίνοντας έτσι από τους φυσικούς αριθμούς προς τους αρνητικούς αριθμούς, έως τα κλάσματα, έως τους πραγματικούς αριθμούς. Η ρίζα του -1, που συνήθως γράφεται i, ολοκλήρωσε αυτή τη διαδικασία, δίνοντας αφορμή για την ανακάλυψη των μιγαδικών αριθμών.
5) Η τετραγωνική ρίζα του –1 (Euler 1750): Οι μαθηματικοί ανέκαθεν ερωτούσαν ποιός πραγματικά να είναι αυτός ο αριθμός, μεταβαίνοντας έτσι από τους φυσικούς αριθμούς προς τους αρνητικούς αριθμούς, έως τα κλάσματα, έως τους πραγματικούς αριθμούς. Η ρίζα του -1, που συνήθως γράφεται i, ολοκλήρωσε αυτή τη διαδικασία, δίνοντας αφορμή για την ανακάλυψη των μιγαδικών αριθμών.
Από μαθηματική άποψη, οι μιγαδικοί αριθμοί είναι εξαιρετικά κομψοί. Η Άλγεβρα λειτουργεί άψογα με τον τρόπο που θέλουμε – και κάθε εξίσωση έχει μια μιγαδική λύση, μια κατάσταση που δεν ισχύει για τους πραγματικούς αριθμούς: Η εξίσωση x2 + 4 = 0 δεν έχει καμία πραγματική λύση, αλλά έχει μόνο μια μιγαδική λύση: τη ρίζα του -4, ή αλλιώς το 2i. Ο λογισμός μπορεί να επεκταθεί στους μιγαδικούς αριθμούς, και με αυτόν τον τρόπο, θα βρείτε μερικές καταπληκτικές συμμετρίες και ιδιότητες αυτών των αριθμών. Αυτές οι ιδιότητες καθιστούν τα πολύπλοκα νούμερα απαραίτητα στα ηλεκτρονικά και στην επεξεργασία του σήματος.
 6) Ο τύπος των πολυέδρων του Euler (1751): Τα πολύεδρα είναι οι τρισδιάστατες εκδόσεις των πολυγώνων, όπως ο κύβος είναι το πολύεδρο του τετραγώνου. Οι γωνίες ενός πολυέδρου ονομάζονται κορυφές, οι γραμμές που συνδέουν τις κορυφές είναι οι ακμές του, και τα πολύγωνα που καλύπτουν αυτό το πολύεδρο είναι οι επιφάνειες του.
6) Ο τύπος των πολυέδρων του Euler (1751): Τα πολύεδρα είναι οι τρισδιάστατες εκδόσεις των πολυγώνων, όπως ο κύβος είναι το πολύεδρο του τετραγώνου. Οι γωνίες ενός πολυέδρου ονομάζονται κορυφές, οι γραμμές που συνδέουν τις κορυφές είναι οι ακμές του, και τα πολύγωνα που καλύπτουν αυτό το πολύεδρο είναι οι επιφάνειες του.
Ένας κύβος για παράδειγμα έχει 8 κορυφές, 12 ακμές, και 6 επιφάνειες. Αν προσθέσετε τις κορυφές και τις επιφάνειες μαζί, και αφαιρέσετε τις ακμές παίρνετε πάντα 2: Έτσι εδώ 8 + 6-12 = 2.
Αυτό θα ισχύει αν το πολύεδρο σας έχει 4, 8, 12, 20 , ή οποιοδήποτε αριθμό επιφανειών.
Η παρατήρηση του Euler ήταν ένα από τα πρώτα παραδείγματα του τι σήμερα ονομάζουμε τοπολογικές αμετάβλητες (ή ιδιότητες) – δηλαδή κάποιοι αριθμοί ή ιδιότητες που μοιράζονται σχήματα που είναι όμοια μεταξύ τους. Σε ολόκληρη την κατηγορία των πολυέδρων θα πρέπει να ισχύει V + F – E = 2 (τοπολογική ιδιότητα των πολυέδρων). Η παρατήρηση αυτή, μαζί με τη λύση του Euler για το πρόβλημα Bridges of Konigsburg, άνοιξε το δρόμο για την ανάπτυξη της τοπολογίας, ενός κλάδου των μαθηματικών απαραίτητο για την σύγχρονη φυσικής.
 7) Κανονική κατανομή (Gauss 1810): Η κανονική κατανομή πιθανοτήτων, η οποία έχει τη γνώριμη κωνοειδή καμπύλη ως γράφημα (αριστερά είναι η εξίσωση της), είναι πανταχού παρούσα στις στατιστικές.
7) Κανονική κατανομή (Gauss 1810): Η κανονική κατανομή πιθανοτήτων, η οποία έχει τη γνώριμη κωνοειδή καμπύλη ως γράφημα (αριστερά είναι η εξίσωση της), είναι πανταχού παρούσα στις στατιστικές.
Η κανονική καμπύλη χρησιμοποιείται στη φυσική, τη βιολογία, καθώς και τις κοινωνικές επιστήμες για να διαμορφώσουν διάφορες ιδιότητες. Ένας από τους λόγους που η κανονική καμπύλη εμφανίζεται τόσο συχνά, είναι ότι περιγράφει τη συμπεριφορά μεγάλων ομάδων ανεξάρτητων διεργασιών.
 8) Κυματική Εξίσωση (J.d’ Albert 1746): Αυτή είναι μια διαφορική εξίσωση, ή μια εξίσωση που περιγράφει πως μία ιδιότητα αλλάζει μέσα στο χρόνο με τη βοήθεια της διπλής παραγώγου, όπως βλέπουμε αριστερά. Η κυματική εξίσωση περιγράφει τη συμπεριφορά των κυμάτων – μια δονούμενη χορδή κιθάρας, οι κυματισμοί σε μια λίμνη αφού πέσει σε αυτήν μια πέτρα, ή το φως που προέρχεται από ένα λαμπτήρα πυρακτώσεως. Η κυματική εξίσωση ήταν μια πρώιμη διαφορική εξίσωση, και οι τεχνικές που αναπτύχθηκαν για την επίλυση της εξίσωσης άνοιξαν την πόρτα για την κατανόηση και άλλων διαφορικών εξισώσεων.
8) Κυματική Εξίσωση (J.d’ Albert 1746): Αυτή είναι μια διαφορική εξίσωση, ή μια εξίσωση που περιγράφει πως μία ιδιότητα αλλάζει μέσα στο χρόνο με τη βοήθεια της διπλής παραγώγου, όπως βλέπουμε αριστερά. Η κυματική εξίσωση περιγράφει τη συμπεριφορά των κυμάτων – μια δονούμενη χορδή κιθάρας, οι κυματισμοί σε μια λίμνη αφού πέσει σε αυτήν μια πέτρα, ή το φως που προέρχεται από ένα λαμπτήρα πυρακτώσεως. Η κυματική εξίσωση ήταν μια πρώιμη διαφορική εξίσωση, και οι τεχνικές που αναπτύχθηκαν για την επίλυση της εξίσωσης άνοιξαν την πόρτα για την κατανόηση και άλλων διαφορικών εξισώσεων.
 9) Μετασχηματισμός Fourier (1822): Ο μετασχηματισμός Fourier είναι απαραίτητος για την κατανόηση πιο σύνθετων κυματικών δομών, όπως η ανθρώπινη ομιλία. Λαμβάνοντας υπόψη μια περίπλοκη, μπερδεμένη, κυματοσυνάρτηση, σαν την κυματομορφή που βλέπουμε στην οθόνη της ομιλίας ενός προσώπου, ο μετασχηματισμός Fourier μας επιτρέπει να σπάσουμε αυτή την περίπλοκη συνάρτηση σε ένα συνδυασμό ενός αριθμού απλών κυμάτων, απλοποιώντας έτσι σημαντικά την ανάλυση.
9) Μετασχηματισμός Fourier (1822): Ο μετασχηματισμός Fourier είναι απαραίτητος για την κατανόηση πιο σύνθετων κυματικών δομών, όπως η ανθρώπινη ομιλία. Λαμβάνοντας υπόψη μια περίπλοκη, μπερδεμένη, κυματοσυνάρτηση, σαν την κυματομορφή που βλέπουμε στην οθόνη της ομιλίας ενός προσώπου, ο μετασχηματισμός Fourier μας επιτρέπει να σπάσουμε αυτή την περίπλοκη συνάρτηση σε ένα συνδυασμό ενός αριθμού απλών κυμάτων, απλοποιώντας έτσι σημαντικά την ανάλυση.
Ο μετασχηματισμός Fourier είναι στο επίκεντρο της σύγχρονης επεξεργασίας σήματος και ανάλυσης, καθώς και της συμπίεσης δεδομένων.
 10) Εξισώσεις Navier-Stokes (1845): Όπως και η κυματική εξίσωση, και αυτή είναι μια διαφορική εξίσωση. Οι εξισώσεις Navier-Stokes περιγράφουν τη συμπεριφορά της ροής των ρευστών – το νερό που περνά μέσω ενός σωλήνα, η ροή του αέρα πάνω από το φτερό ενός αεροπλάνου, ή ο καπνός που βγαίνει από ένα τσιγάρο. Ενώ έχουμε προσεγγιστικά λύσεις των εξισώσεων Navier-Stokes, που επιτρέπουν στους υπολογιστές να προσομοιώσουν την κίνηση του ρευστού αρκετά καλά, εξακολουθεί να είναι ένα ανοικτό ερώτημα (με χρηματικό έπαθλο εκατομμυρίων δολαρίων) κατά πόσον είναι δυνατόν να κατασκευαστούν μαθηματικά ακριβές λύσεις στις εξισώσεις.
10) Εξισώσεις Navier-Stokes (1845): Όπως και η κυματική εξίσωση, και αυτή είναι μια διαφορική εξίσωση. Οι εξισώσεις Navier-Stokes περιγράφουν τη συμπεριφορά της ροής των ρευστών – το νερό που περνά μέσω ενός σωλήνα, η ροή του αέρα πάνω από το φτερό ενός αεροπλάνου, ή ο καπνός που βγαίνει από ένα τσιγάρο. Ενώ έχουμε προσεγγιστικά λύσεις των εξισώσεων Navier-Stokes, που επιτρέπουν στους υπολογιστές να προσομοιώσουν την κίνηση του ρευστού αρκετά καλά, εξακολουθεί να είναι ένα ανοικτό ερώτημα (με χρηματικό έπαθλο εκατομμυρίων δολαρίων) κατά πόσον είναι δυνατόν να κατασκευαστούν μαθηματικά ακριβές λύσεις στις εξισώσεις.
 11) Εξισώσεις του Maxwell (1865): Αυτό το σύνολο των τεσσάρων διαφορικών εξισώσεων περιγράφει τη συμπεριφορά και τη σχέση μεταξύ της ηλεκτρικής ενέργειας (Ε) και του μαγνητισμού (H).
11) Εξισώσεις του Maxwell (1865): Αυτό το σύνολο των τεσσάρων διαφορικών εξισώσεων περιγράφει τη συμπεριφορά και τη σχέση μεταξύ της ηλεκτρικής ενέργειας (Ε) και του μαγνητισμού (H).
Οι εξισώσεις του Maxwell είναι για τον κλασσικό ηλεκτρομαγνητισμό, όπως είναι οι νόμοι του Νεύτωνα και ο νόμος της παγκόσμιας έλξης στην κλασική μηχανική – είναι το θεμέλιο της εξήγησης του πώς λειτουργεί ο ηλεκτρομαγνητισμός σε κανονική κλίμακα Όπως θα δούμε, όμως, η σύγχρονη φυσική βασίζεται σε μια κβαντική μηχανική εξήγηση του ηλεκτρομαγνητισμού, και είναι πλέον σαφές ότι αυτές οι κομψές εξισώσεις είναι απλώς μια προσέγγιση που λειτουργούν καλά αλλά για την ανθρώπινη κλίμακα.
 12) Δεύτερος Νόμος της Θερμοδυναμικής (Boltzmann 1874): Η εξίσωση αυτή δηλώνει ότι, σε ένα κλειστό σύστημα, η εντροπία (S) είναι πάντα σταθερή ή αυξάνεται. Η θερμοδυναμική εντροπία είναι, σε γενικές γραμμές, ένα μέτρο της αταξίας ενός συστήματος. Ένα σύστημα που ξεκινά με μία τάξη, αλλά με άνιση κατανομή – ας πούμε, μια θερμή περιοχή δίπλα σε μία κρύα περιοχή – θα έχουν πάντα την τάση οι περιοχές αυτές να εξομαλύνουν τις θερμοκρασίες τους, με τη θερμότητα να ρέει από το ζεστό χώρο στην ψυχρή περιοχή μέχρι η θερμοκρασία να κατανέμεται ομοιόμορφα.
12) Δεύτερος Νόμος της Θερμοδυναμικής (Boltzmann 1874): Η εξίσωση αυτή δηλώνει ότι, σε ένα κλειστό σύστημα, η εντροπία (S) είναι πάντα σταθερή ή αυξάνεται. Η θερμοδυναμική εντροπία είναι, σε γενικές γραμμές, ένα μέτρο της αταξίας ενός συστήματος. Ένα σύστημα που ξεκινά με μία τάξη, αλλά με άνιση κατανομή – ας πούμε, μια θερμή περιοχή δίπλα σε μία κρύα περιοχή – θα έχουν πάντα την τάση οι περιοχές αυτές να εξομαλύνουν τις θερμοκρασίες τους, με τη θερμότητα να ρέει από το ζεστό χώρο στην ψυχρή περιοχή μέχρι η θερμοκρασία να κατανέμεται ομοιόμορφα.
Ο δεύτερος νόμος της θερμοδυναμικής είναι μία από τις λίγες περιπτώσεις της φυσικής, όπου ο χρόνος συμπεριφέρεται με αυτόν τον τρόπο. Οι περισσότερες φυσικές διεργασίες είναι αντιστρέψιμες – μπορούμε να τρέξουμε τις εξισώσεις προς τα πίσω, χωρίς να πειράξουμε τα πράγματα. Ο δεύτερος νόμος, ωστόσο, τρέχει μόνο προς σε αυτή την κατεύθυνση. Αν βάλουμε ένα παγάκι σε ένα φλιτζάνι ζεστό καφέ, βλέπουμε πάντα την τήξη του πάγου, και ποτέ δε βλέπουν το πάγωμα του καφέ.

13) Σχετικότητα (1905-1915): Ο Einstein άλλαξε ριζικά την πορεία της φυσικής με τις θεωρίες του ειδική και γενική σχετικότητα. Η κλασική εξίσωση E = mc2 αναφέρει ότι η ύλη και η ενέργεια είναι ισοδύναμες μεταξύ τους. Η ειδική σχετικότητα έφερε ιδέες όπως ότι η ταχύτητα του φωτός είναι ένα καθολικό όριο της ταχύτητας στο σύμπαν και το πέρασμα του χρόνου είναι διαφορετικό για τους ανθρώπους που κινούνται με διαφορετικές ταχύτητες.
Η γενική σχετικότητα περιγράφει τη βαρύτητα σαν μια κάμψη και σαν αναδίπλωση του χώρου και του χρόνου στον εαυτό τους, και ήταν η πρώτη μεγάλη αλλαγή στην κατανόησή της βαρύτητας μετά από το νόμο του Νεύτωνα. Η γενική σχετικότητα είναι απαραίτητη για την κατανόηση της προέλευσης, τη δομή και την τελευταία μοίρα του σύμπαντος.
 14) Εξίσωση του Schrödinger (1927): είναι η κύρια εξίσωση στην κβαντομηχανική. Όπως η γενική σχετικότητα εξηγεί το σύμπαν μας σε μεγαλύτερες κλίμακες, αυτή η εξίσωση διέπει τη συμπεριφορά των ατόμων και των υποατομικών σωματιδίων.
14) Εξίσωση του Schrödinger (1927): είναι η κύρια εξίσωση στην κβαντομηχανική. Όπως η γενική σχετικότητα εξηγεί το σύμπαν μας σε μεγαλύτερες κλίμακες, αυτή η εξίσωση διέπει τη συμπεριφορά των ατόμων και των υποατομικών σωματιδίων.
Η σύγχρονη κβαντομηχανική και η γενική σχετικότητα είναι οι δύο πιο επιτυχημένες επιστημονικές θεωρίες στην ιστορία – όλες οι πειραματικές παρατηρήσεις που έχουμε κάνει μέχρι στιγμής είναι απόλυτα συνεπείς με τις προβλέψεις τους. Η κβαντομηχανική είναι επίσης απαραίτητη για την πιο σύγχρονη τεχνολογία – πυρηνική ενέργεια, οι υπολογιστές που βασίζονται σε ημιαγωγούς, αλλά και τα λέιζερ είναι όλα χτισμένα γύρω από τα κβαντικά φαινόμενα.
 15) Θεωρία Πληροφορίας (Shannon 1949) : Η εξίσωση που δίνεται εδώ είναι για την εντροπία της πληροφορίας του Σάνον. Όπως και με την θερμοδυναμική εντροπία που είπαμε παραπάνω, είναι κι αυτή ένα μέτρο της αταξίας. Σε αυτή την περίπτωση, όμως, μετρά το πληροφοριακό περιεχόμενο ενός μηνύματος – ένα βιβλίο, μια εικόνα JPEG που αποστέλλονται στο διαδίκτυο, ή οτιδήποτε που μπορεί να αναπαρασταθεί συμβολικά. Η εντροπία κατά Shannon ενός μηνύματος αντιπροσωπεύει ένα κάτω φράγμα για το πόσο το μήνυμα αυτό μπορεί να συμπιεστεί χωρίς να χαθούν μερικά στοιχεία από το περιεχόμενό του.
15) Θεωρία Πληροφορίας (Shannon 1949) : Η εξίσωση που δίνεται εδώ είναι για την εντροπία της πληροφορίας του Σάνον. Όπως και με την θερμοδυναμική εντροπία που είπαμε παραπάνω, είναι κι αυτή ένα μέτρο της αταξίας. Σε αυτή την περίπτωση, όμως, μετρά το πληροφοριακό περιεχόμενο ενός μηνύματος – ένα βιβλίο, μια εικόνα JPEG που αποστέλλονται στο διαδίκτυο, ή οτιδήποτε που μπορεί να αναπαρασταθεί συμβολικά. Η εντροπία κατά Shannon ενός μηνύματος αντιπροσωπεύει ένα κάτω φράγμα για το πόσο το μήνυμα αυτό μπορεί να συμπιεστεί χωρίς να χαθούν μερικά στοιχεία από το περιεχόμενό του.
Η εντροπίας του Shannon ξεκίνησε τη μαθηματική μελέτη των πληροφοριών, και τα αποτελέσματά της είναι κεντρικής σημασίας για τον τρόπο που επικοινωνούμε μέσω των δικτύων σήμερα.
 16) Θεωρία του Χάους (1975): Αυτή η εξίσωση είναι λογιστική απεικόνιση που δημιούργησε ο βιολόγος Robert May. Περιγράφει μια διαδικασία εν εξελίξει, στο πέρασμα του χρόνου – xt+1, είναι η τιμή κάποιας ποσότητας x στο επόμενο χρονικό διάστημα – και δίνεται από την φόρμουλα δεξιά, και φυσικά αυτή η τιμή εξαρτάται από την τιμή xt, την τωρινή τιμή του x. Η k είναι μια επιλεγμένη σταθερά. Για ορισμένες τιμές του k, η απεικόνιση δείχνει χαοτική συμπεριφορά: αν αρχίσουμε με κάποια συγκεκριμένη αρχική τιμή του x, η διαδικασία θα εξελιχθεί μονόδρομα, αλλά αν αρχίσουμε με άλλη αρχική τιμή, ακόμα και με μια τιμή πολύ πολύ κοντά στην πρώτη τιμή, η διαδικασία θα εξελιχθεί με ένα εντελώς διαφορετικό τρόπο.
16) Θεωρία του Χάους (1975): Αυτή η εξίσωση είναι λογιστική απεικόνιση που δημιούργησε ο βιολόγος Robert May. Περιγράφει μια διαδικασία εν εξελίξει, στο πέρασμα του χρόνου – xt+1, είναι η τιμή κάποιας ποσότητας x στο επόμενο χρονικό διάστημα – και δίνεται από την φόρμουλα δεξιά, και φυσικά αυτή η τιμή εξαρτάται από την τιμή xt, την τωρινή τιμή του x. Η k είναι μια επιλεγμένη σταθερά. Για ορισμένες τιμές του k, η απεικόνιση δείχνει χαοτική συμπεριφορά: αν αρχίσουμε με κάποια συγκεκριμένη αρχική τιμή του x, η διαδικασία θα εξελιχθεί μονόδρομα, αλλά αν αρχίσουμε με άλλη αρχική τιμή, ακόμα και με μια τιμή πολύ πολύ κοντά στην πρώτη τιμή, η διαδικασία θα εξελιχθεί με ένα εντελώς διαφορετικό τρόπο.
Βλέπουμε χαοτική συμπεριφορά – δηλαδή συμπεριφορά ευαίσθητη στις αρχικές συνθήκες – σαν και αυτή σε πολλά πεδία. Ο καιρός είναι ένα κλασικό παράδειγμα – μια μικρή αλλαγή στις ατμοσφαιρικές συνθήκες σε μία ημέρα μπορεί να οδηγήσει σε εντελώς διαφορετικά καιρικά συστήματα λίγες μέρες αργότερα, πιο συχνά αναφερόμαστε στο πέταγμα μιας πεταλούδας, σε μία ήπειρο που προκαλεί έναν τυφώνα σε μια άλλη ήπειρο.
 17) Εξίσωση Black-Scholes (1990): Άλλη μία διαφορική εξίσωση, που περιγράφει πώς οι οικονομικοί ειδικοί και οι traders βρίσκουν τιμές για τα παράγωγα. Τα παράγωγα – είναι χρηματοοικονομικά προϊόντα που βασίζονται σε κάποιο υποκείμενο στοιχείο ενεργητικού, όπως ένα απόθεμα – και είναι ένα σημαντικό μέρος του σύγχρονου χρηματοπιστωτικού συστήματος.
17) Εξίσωση Black-Scholes (1990): Άλλη μία διαφορική εξίσωση, που περιγράφει πώς οι οικονομικοί ειδικοί και οι traders βρίσκουν τιμές για τα παράγωγα. Τα παράγωγα – είναι χρηματοοικονομικά προϊόντα που βασίζονται σε κάποιο υποκείμενο στοιχείο ενεργητικού, όπως ένα απόθεμα – και είναι ένα σημαντικό μέρος του σύγχρονου χρηματοπιστωτικού συστήματος.
Η εξίσωση Black-Scholes επιτρέπει στους εξπέρ περί τα χρηματοπιστωτικά, τον υπολογισμό της αξίας αυτών των χρηματοοικονομικών προϊόντων, με βάση τις ιδιότητες του παραγώγου και του υποκείμενου περιουσιακού στοιχείου.
Δείτε και ένα σχετικό βίντεο


