Γιατί σε σημεία που το βαρυτικό πεδίο είναι ισχυρότερο, τα ρολόγια “τρέχουν” με πιο αργούς ρυθμούς; Η απάντηση βρίσκεται στα πλαίσια της Γενικής σχετικότητας και μπορούμε να δώσουμε μια απλή εξήγηση χωρίς να καταφύγουμε στις γενικές εξισώσεις πεδίου του Einstein. Ένα από τα κεντρικά σημεία στα οποία στηρίχτηκε η Γενική Σχετικότητα, είναι η λεγόμενη αρχή της ισοδυναμίας. Αυτή λέει ότι όλοι οι νόμοι της φυσικής έχουν την ίδια μορφή σε ένα σύστημα αναφοράς που εκτελεί ελεύθερη πτώση, με αυτή που θα είχαν σε ένα σύστημα αναφοράς εκτός πεδίου βαρύτητας.
Η αρχή αυτή εύκολα μπορεί να μας οδηγήσει και σε ένα άλλο συμπέρασμα. Ότι δηλαδή ένα σύστημα που επιταχύνεται προς μια κατεύθυνση με επιτάχυνση g είναι ισοδύναμο με ένα άλλο ακίνητο, που βρίσκεται μέσα σε πεδίο βαρύτητας έντασης έντασης ίσης με g, και αντίθετης φοράς. Αυτή η απλή πρόταση έχει πολλές και σημαντικές συνέπειες, μια από τις οποίες είναι και η διαστολή του χρόνου από το πεδίο βαρύτητας.
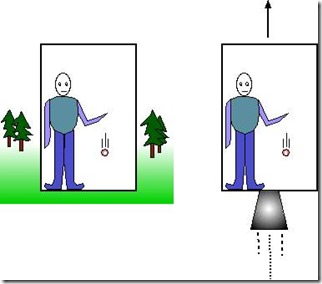
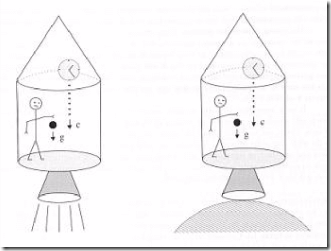
Ας θεωρήσουμε ένα σύστημα αναφοράς, όπως λ.χ. ένα πύραυλο ύψους h που κινείται προς τα επάνω με επιτάχυνση g (αριστερό μέρος του σχήματος), και ένα ρολόι στο επάνω μέρος του πυραύλου, που στέλνει φωτόνια προς το πάτωμα με σταθερό ρυθμό. Η συχνότητα των φωτονίων αυτών – πιο σωστά η περίοδός τους – χρησιμοποιείται ως μονάδα για τη μέτρηση του χρόνου από το ρολόι αυτό.
Αν ο πύραυλος επιταχύνεται προς τα επάνω με g, τότε το δάπεδο μέσα στο χρόνο που χρειάζεται ένα φωτόνιο για να φτάσει από την οροφή στο δάπεδο, θα έχει αποκτήσει ταχύτητα
v=gh/c όπου c είναι η ταχύτητα του φωτός η οποία είναι σταθερή.
Σύμφωνα τότε με το φαινόμενο Doppler για το φως, το φως όταν θα φτάσει στο πάτωμα, θα έχει υποστεί μια μετατόπιση συχνότητας προς το μπλε που δίνεται σε πρώτη προσέγγιση από τη σχέση:
Δf = vf/c ή Δf=ghf/c2 ή Δf/f = gh/c2 όπου f είναι η συχνότητα των φωτονίων που στέλνει το ρολόι-πηγή της οροφής.
Είναι εύκολο να δούμε ότι η σχετική αυτή μεταβολή της συχνότητας αντιπροσωπεύει επίσης τον αυξημένο ρυθμό καταγραφής των φωτονίων όπως τον μετράει ένας παρατηρητής στο δάπεδο.
Ο παρατηρητής λοιπόν του δαπέδου, αν διαθέτει ένα πανομοιότυπο ρολό με αυτό της οροφής είναι αναγκασμένος να συμπεράνει ότι, το ρολόι της οροφής τρέχει με γρηγορότερο ρυθμό από το δικό του, κι έτσι εξηγεί την υψηλότερη συχνότητα των φωτονίων που λαμβάνει.
Αν λοιπόν υποτεθεί ότι η επιτάχυνση διαρκεί κάποιο χρονικό διάστημα t σύμφωνα με το ρολόι της οροφής, ο παρατηρητής του δαπέδου θα αντιλαμβάνεται ότι το ρολόι της οροφής έχει προηγηθεί του δικού του κατά Δt σύμφωνα με τη σχέση:
Δt/t = gh/c2
Με άλλα λόγια, αντιλαμβάνεται ότι το ρολόι της οροφής πηγαίνει πιο γρήγορα από το δικό του ή ότι το δικό του είναι πιο αργό – μένει πίσω.
Αν επικαλεστούμε τώρα την αρχή της ισοδυναμίας που αναφέραμε στην αρχή, καταλήγουμε στο συμπέρασμα ότι και η βαρύτητα φέρνει το ίδιο αποτέλεσμα. Ένας παρατηρητής στο δάπεδο ενός ακίνητου πυραύλου που βρίσκεται ακίνητος στο πεδίο βαρύτητας ας πούμε της Γης, θα αντιλαμβάνεται ότι το δικό του ρολόι πάει πίσω σε σχέση με ένα ρολόι που βρίσκεται υψηλότερα στην κορυφή του πυραύλου. (Δεξιό μέρος του σχήματος).
μάλιστα αν θυμηθούμε ότι η διαφορά δυναμικού μεταξύ δύο σημείων με υψομετρική διαφορά h σ’ ένα π.χ. ομογενές πεδίο βαρύτητας δίνεται από τη σχέση:
Δφ = gh
τότε καταλήγουμε στη σχέση που δίνει τη διαστολή του χρόνου μέσα στο πεδίο βαρύτητας:
Δt/t = Δφ/c2
Η πειραματική επαλήθευση της μετατόπισης Doppler της συχνότητας του φωτός λόγω πεδίου βαρύτητας, και συνεπώς της επιβεβαίωσης της αρχής της ισοδυναμίας, έγινε ήδη από τη δεκαετία του 1960.
Πειραματική απόδειξη για την διαστολή του χρόνου που προβλέπει η σχετικότητα
Η ειδική σχετικότητα προβλέπει ότι αν δύο γεγονότα τα καταγράφουν τα ρολόγια δύο διαφορετικών παρατηρητών, για τον ένα εκ των οποίων τα γεγονότα αυτά συμβαίνουν στην ίδια θέση στον χώρο ενώ για τον άλλον συμβαίνουν σε διαφορετικές θέσεις, η χρονική διαφορά των γεγονότων ως προς τον πρώτο παρατηρητή θα είναι μεγαλύτερη από αυτήν που κατέγραψε ο δεύτερος. Το φαινόμενο αυτό της επιμήκυνσης του χρόνου ονομάζεται διαστολή του χρόνου.
Υπάρχουν διάφορες αποδείξεις για την διαστολή αυτή του χρόνου. Για παράδειγμα, ρολόγια εξαιρετικής ακρίβειας επιβιβάστηκαν σε ταχύτατα αεροπλάνα. Όταν μετά συγκρίθηκαν οι ενδείξεις τους με αντίστοιχα ρολόγια που είχαν παραμείνει επί του εδάφους και είχαν αρχικά συγχρονιστεί με τα ιπτάμενα, βρέθηκε ότι τα ιπτάμενα ρολόγια είχαν καταγράψει ελαφρά μικρότερα χρονικά διαστήματα.
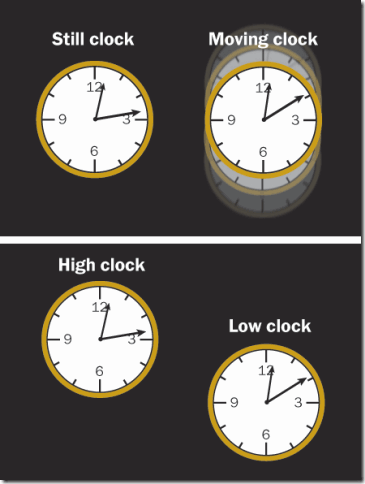Διαστολή χρόνου λόγω ταχύτητας και διαστολή χρόνου λόγω βαρυτικού πεδίου
Τον Οκτώβριο του 1971, οι πειραματιστές Hafele και Keating, χρησιμοποίησαν ατομικά ρολόγια Καισίου, τα οποία αφού πρώτα συντόνισαν με ατομικά ρολόγια του Ναυτικού παρατηρητηρίου στην Washington, επιβίβασαν στη συνέχεια σε αεροπλάνα, τα οποία πέταξαν το μεν ένα προς την ανατολή και το δεύτερο προς τη δύση. Μετά από κάθε πτήση συνέκριναν το χρόνο που κατέγραψε το ρολόι επί του αεροσκάφους, με τον χρόνο που κατέγραψε το ρολόι του παρατηρητηρίου του Ναυτικού. Τα πειραματικά δεδομένα συμφωνούσαν μέσα στα όρια του πειραματικού σφάλματος με τις προβλέψεις της Γενικής Σχετικότητας. Πιο συγκεκριμένα, το χρονόμετρο που πέταξε προς δυσμάς κατέγραψε χρονικό διάστημα μεγαλύτερο από αυτό που κατέγραψε το δίδυμο χρονόμετρο που πέταξε προς ανατολάς. Φυσικά οι διαφορές αυτές ήταν πολύ μικρές επειδή τα αεροπλάνα πετούν με ταχύτητες πάρα πολύ μικρότερες από αυτήν του φωτός.
Ένα άλλο πείραμα που μας πείθει για την διαστολή του χρόνου, στηρίζεται στη διάσπαση ορισμένων σωματιδίων. Τέτοια σωματίδια που διασπώνται σε άλλα σωματίδια είναι τα μιόνια, τα οποία σχηματίζονται από την αλληλεπίδραση των κοσμικών ακτίνων με τα στρώματα της ανώτερης ατμόσφαιρας.
Όταν βρίσκονται σε ηρεμία τα σωματίδια αυτά διασπώνται περίπου σε χρόνο t = 2 x 10-6 sec, χρόνος ο οποίος είναι πολύ μικρός για να προλάβουν να φτάσουν αδιάσπαστα μέχρι την επιφάνεια της Γης. Επειδή όμως ταξιδεύουν με ταχύτητες οι οποίες συγκρίνονται με εκείνη του φωτός, ο χρόνος της ζωής τους t‘ όπως μετρείται από ένα γήινο παρατηρητή ο οποίος τα καταγράφει σε δύο διαφορετικές θέσεις (θέση δημιουργίας και θέση καταστροφής τους), έχει διασταλεί σε σχέση με τον χρόνο ζωής του συστήματος ηρεμίας τους. Έτσι ο παρατηρητής αυτός μπορεί να εξηγήσει πως προλαβαίνουν και φτάνουν τα σωματίδια αυτά μέχρι τη Γη.
