Γνωρίζουμε πως αν ένα σώμα, πχ ένας πλανήτης ή ένας δορυφόρος, τοποθετηθεί σε ένα σημείο του πεδίου βαρύτητας δύο άλλων ουράνιων σωμάτων και η συνολική δύναμη που εξασκείται πάνω στο σώμα είναι μηδέν, τότε θα ισορροπήσει. Κάθε τέτοιο σημείο ονομάζεται σημείο ισορροπίας Λαγκράνζ. Για παράδειγμα, ανάμεσα σε δύο ουράνια σώματα, υπάρχει πάντα ένα σημείο ισορροπίας, στο οποίο αν τοποθετηθεί ένας δορυφόρος, θα δέχεται συνολική βαρυτική δύναμη μηδέν, αν συνυπολογιστεί βέβαια και η φυγόκεντρος δύναμη.
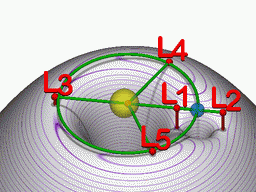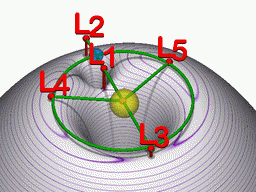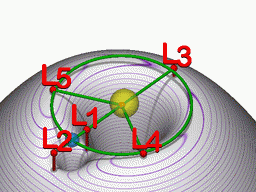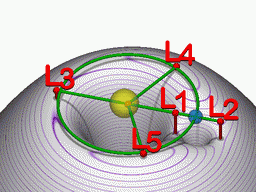
Απεικόνιση σχέσης μεταξύ σημείων Λαγκράνζ (κόκκινο), ενός πλανήτη (μπλε) σε αριστερόστροφη τροχιά γύρω από ένα αστέρι (κίτρινο) και το ενεργό δυναµικό στο επίπεδο της τροχιάς.
Μπορούμε βέβαια να πούμε πως η συνολική έλξη που δέχεται ένας δορυφόρος στα σημεία αυτά είναι ίση με την απαραίτητη κεντρομόλο δύναμη για να περιστρέφεται.
Ευσταθή και ασταθή σημεία ισορροπίας
Υπάρχουν δύο είδη σημείων ισορροπίας. Τα ευσταθή και τα αστασθή σημεία. Αν ένας δορυφόρος τοποθετηθεί σε κάποιο σημείο ευσταθούς ισορροπίας με μικρή ταχύτητα, τότε το σώμα θα έχει την τάση να επιστρέφει, σε κάθε περίπτωση, στο σημείο ευσταθούς ισορροπίας, παραμένοντας, έτσι, για πάντα στην περιοχή γύρω από αυτό.
Αν όμως το σημείο είναι ασταθές, τότε με την πάροδο του χρόνου ο δορυφόρος θα απομακρύνεται σταδιακά από την περιοχή ασταθούς ισορροπίας και δε θα επιστρέψει ποτέ.
Θεωρούμε λοιπόν ένα σώμα (πλανήτη ή δορυφόρο) που κινείται σε κυκλική τροχιά (ή σχεδόν κυκλική) τροχιά γύρω από ένα άλλο (πλανήτη ή άστρο). Τότε υπάρχουν, ανάμεσά τους, καθορισμένα σημεία ισορροπίας, σε σχέση με την ευθεία που τα ενώνει.
Την ύπαρξη των σημείων αυτών είχε προβλέψει ο Γάλλος μαθηματικός και αστρονόμος Louis Lagrange (Λαγκρανζ), από το 1772. Συνολικά, υπάρχουν 5 τέτοια σημεία ισορροπίας για ένα σύστημα δύο ουρανίων σωμάτων (πχ. Γη-Ήλιος ή Γη-Σελήνη).
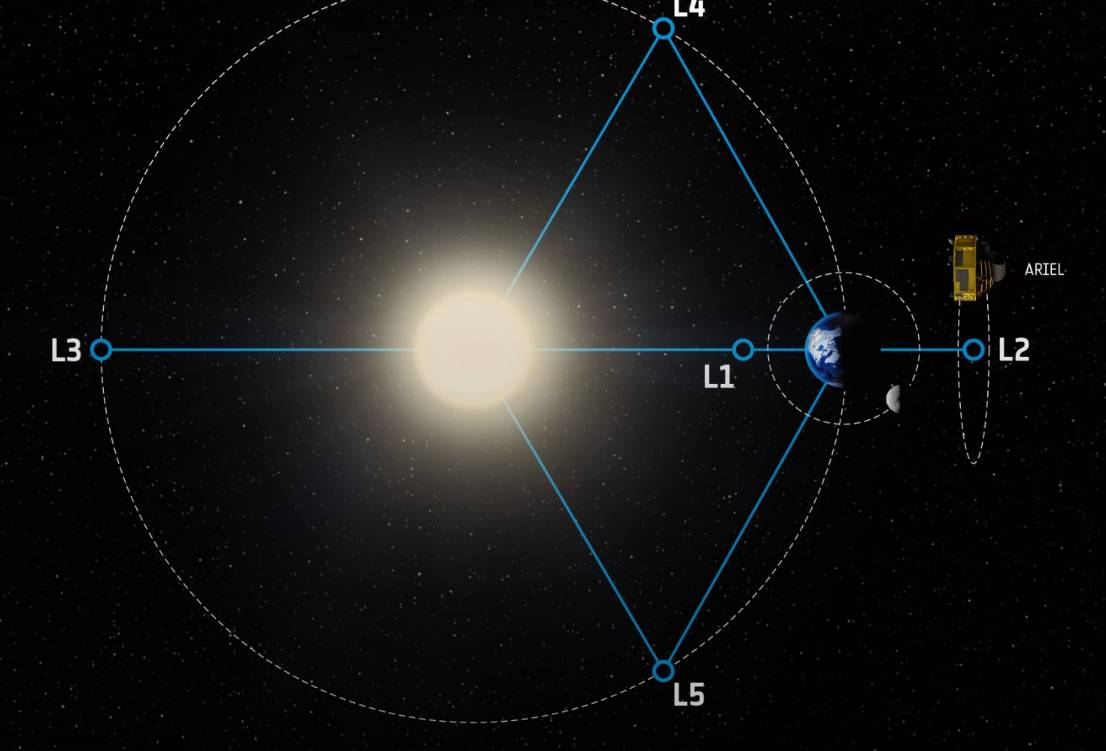
Τα τρία σημεία από αυτά (L1 – L2 – L3), βρίσκονται πάνω στην ευθεία που ενώνει τα δύο ουράνια σώματα, ενώ τα υπόλοιπα (L4 – L5), βρίσκονται πάνω στις κορυφές ενός ισόπλευρου τριγώνου. Σε αυτά σημεία, η συνολική δύναμη που δέχεται ένας δορυφόρος, που περιστρέφεται, από τ’ άλλα δύο ουράνια σώματα, είναι ίση με την κεντρομόλο δύναμη.
Τα σημεία L1, L2, L3 είναι ασταθή σημεία ισορροπίας. Γι’ αυτό, ένας δορυφόρος που θα τοποθετηθεί σε μία από αυτές τις τρεις θέσεις, θα πρέπει ανά τακτά χρονικά διαστήματα να πυροδοτεί τους κινητήρες του, ώστε να αποτρέπει την οποιαδήποτε διαταραχή στην ταχύτητα του (που μπορεί να προέρχεται από πολλούς παράγοντες), που θα το απομακρύνει από την περιοχή του σημείου ισορροπίας.
Για το σύστημα Γης – Ήλιου, όμως, αν και τα τρία αυτά σημεία είναι ασταθή, ορίζεται μια σταθερή τροχιά, γύρω από αυτά.
Όμως τα L4, L5 αντίθετα είναι ευσταθή σημεία ισορροπίας, γι’ αυτό και οποιοδήποτε σώμα βρεθεί με μηδενική ταχύτητα στην περιοχή ενός από αυτά τα σημεία, δεν θα μπορεί να ξεφύγει ποτέ από εκεί. Χαρακτηριστικό παράδειγμα είναι οι ομάδες των Τρωικών Αστεροειδών που βρίσκονται παγιδευμένοι στα σημεία L4, L5 του συστήματος Δία – Ηλίου και που ανακαλύφθηκε το 1906.
Καθένα από τα L4, L5 , που αποτελούν τα σταθερά σημεία Λαγκρανζ, αποτελούν την μια κορυφή ενός ισοπλεύρου τριγώνου, που στις δύο άλλες του κορυφές, βρίσκονται τα δύο ουράνια σώματα των οποίων οι βαρυτικές δυνάμεις ισορροπούν στο σημείο L4 ή L5 .
Χρησιμοποίηση των σημείων Lagrange στις διαστημικές αποστολές
Το γεγονός πως τα σημεία Lagrange είναι σημεία ισορροπίας και έχουν σταθερή θέση ως προς ένα σύστημα ουρανίων σωμάτων, τα κάνει χρήσιμα, για πολλούς σκοπούς, στους σχεδιαστές των διαστημικών αποστολών :
Το σημείο L1 του συστήματος Γης – Ηλίου βρίσκεται πάνω στην ευθεία των δύο σωμάτων και προς την πλευρά του Ήλιου, οπότε τα διαστημόπλοια που τοποθετούνται σε σταθερή τροχιά γύρω απ’ αυτόν, να μπορούν να καταγράφουν τα χαρακτηριστικά του ηλιακού ανέμου, προτού αυτός φτάσει στη Γη. ένα παράδειγμα αποτελεί ο επιστημονικός δορυφόρος της ESA, MAP, SOHO αλλά και το Genesis που τέθηκε σε μια τροχιά γύρω από το σημείο ισορροπίας Lagrange L1.
Όλα τα σημεία Lagrange του συστήματος Γης – Ηλίου (εκτός του σημείου L3) μπορούν να χρησιμοποιηθούν ως περιοχές τοποθέτησης μεγάλων διαστημικών τηλεσκοπίων. Οι θέσεις αυτές προσφέρονται για εύκολη επικοινωνία με τη Γη αλλά και για καλύτερες και περισσότερες παρατηρήσεις, καθώς στο οπτικό πεδίο του τηλεσκοπίου δε θα παρεμβάλλεται ο γήινος όγκος, όπως συμβαίνει με το Hubble (αφού όλα τα σημεία Lagrange Γης – Ηλίου βρίσκονται τουλάχιστον 1,5 εκατ. χλμ. από τη Γη). Ήδη, το επόμενο μεγάλο διαστημικό τηλεσκόπιο που σχεδιάζεται (Next Generation Space Telescope), προβλέπεται να τοποθετηθεί σε σταθερή τροχιά γύρω από το σημείο L2 του συστήματος Γης – Ηλίου.
Το γεγονός πως τα σημεία Lagrange είναι σημεία ισορροπίας, σημαίνει πως στην περιοχή τους η βαρυτική δύναμη είναι σχεδόν ανύπαρκτη. Δηλαδή ένας δορυφόρος που ξεκινάει το ταξίδι του από εκεί, μπορεί με μια μικρή μεταβολή της ταχύτητας του (δηλαδή χωρίς μεγάλη κατανάλωση καυσίμων) να αλλάξει σημαντικά την τροχιά του.
Σχεδιάγραμμα του πραγματικού δυναμικού ενός συστήματος δύο σωμάτων ( εδώ, του Ήλιου και της Γης ) που οφείλεται στην βαρύτητα και την φυγόκεντρο δύναμη, όπως φαίνεται από ένα περιστρεφόμενο πλαίσιο αναφοράς όπου τα δύο σώματα μένουν σταθερά. Καθώς η Γη θ’ αρχίσει να κινείται σύμφωνα με τις ισοϋψείς καμπύλες, τα αντικείμενα που περιστρέφονται με την ίδια περιστροφική περίοδο, θα παρουσιάζουν ισοδυναμικές επιφάνειες. Με τα βέλη σημειώνονται οι κλίσεις του δυναμικού γύρω από τα πέντε σημεία Lagrange — κάτω και προς αυτά ( κόκκινο ) ή μακριά τους ( μπλε ). Στα ίδια τα σημεία, οι δυνάμεις αυτές ισορροπούν.
Πηγή στοιχείων : Wikipedia.
