H θεωρία της βαρύτητας του Αϊνστάιν

Χώρος – Χρόνος και βαρύτητα

Στη Νευτώνεια θεωρία η βαρύτητα αντιμετωπίζεται σαν ένα πεδίο το οποίο είναι ανάλογο ως προς πολλές από τις ιδιότητες του με ένα ηλεκτρικό πεδίο. Ωστόσο, υπάρχουν δύο βασικές ιδέες οι οποίες οδηγούν στη σκέψη ότι ίσως η βαρύτητα είναι διαφορετική από τα άλλα πεδία.

Πρώτον, η βαρύτητα είναι παγκόσμια. Όλα τα σώματα επηρεάζονται από αυτήν. Σε αντίθεση, τα ηλεκτρικά πεδία δεν επηρεάζουν σώματα που είναι ηλεκτρικά ουδέτερα. Επίσης, όλα τα σώματα πέφτουν με τον ίδιο τρόπο μέσα σε ένα βαρυτικό πεδίο. Αυτό το γεγονός, γνωστό ως αρχή της ισοδυναμίας, εκφράζεται στη Νευτώνεια θεωρία από την πρόταση ότι η βαρυτική δύναμη σε ένα σώμα είναι ανάλογη της μάζας του, οπότε η επιτάχυνση που υφίσταται είναι ανεξάρτητη της μάζας του. H αρχή της ισοδυναμίας ουσιαστικά οφείλεται στον Γαλιλαίο με το διάσημο πείραμα του να ρίξει δύο σώματα διαφορετικού βάρους από τον πύργο της Πίζας.

Τι σημασία έχει αυτή η παγκοσμιότητα της βαρύτητας; Υπονοεί ότι θα μπορούσε κανείς να αποδώσει τις ιδιότητες του βαρυτικού πεδίου σε μία άλλη εξίσου παγκόσμια οντότητα, το χωροχρόνο!

Μία δεύτερη, μάλλον ασαφής, σειρά ιδεών αφορά την έννοια της αδράνειας και συνήθως αποκαλείται αρχή του Μαχ, αν και πολλές από τις σχετικές ιδέες είναι παλαιότερες του Μαχ (ο οποίος τις διατύπωσε στα τέλη του 19ου αιώνα). H βασική ιδέα είναι η εξής: Θεωρούμε ένα περιστρεφόμενο σώμα. Μπορεί κανείς να μετρήσει την περιστροφή με δύο διαφορετικούς τρόπους: 1ον με μία απόλυτη και τοπική μέθοδο, μετρώντας τις τάσεις (δυνάμεις) στο σώμα που είναι απαραίτητες ώστε να συγκρατήσουν τα εξωτερικά μέρη του ώστε να μη διαφύγουν, ή 2ον σε σχέση με ύλη που βρίσκεται μακριά (για παράδειγμα καθορισμένα αστέρια).

Γιατί συμφωνούν αυτές οι δύο έννοιες περιστροφής; H ιδέα του Μαχ ήταν ότι η απομακρυσμένη ύλη στο σύμπαν καθορίζει τα τοπικά αδρανειακά φαινόμενα που σχετίζονται με την περιστροφή. Οπότε, αν κανείς μπορούσε με οποιονδήποτε τρόπο να επιταχύνει την απομακρυσμένη ύλη του σύμπαντος, θα επηρεάζονταν άμεσα οι τοπικοί μας προσδιορισμοί σε σχέση με την επιτάχυνση ή την περιστροφή. Αν δεν υπήρχε καθόλου ύλη στο υπόλοιπο σύμπαν, δεν θα έπρεπε να υπάρχει ούτε αδράνεια ούτε περιστροφή.

O Αϊνστάιν αποδέχτηκε τη βασική ιδέα της αρχής του Μαχ. Ωστόσο, οι ιδέες του Μαχ δεν μπορούν να εφαρμοστούν στην ειδική θεωρία της σχετικότητας, όπου η δομή του χωροχρόνου δεν επηρεάζεται από την ύλη. Αυτό προσέφερε ένα κίνητρο στον Αϊνστάιν να αναζητήσει μία νέα θεωρία, στην οποία τα βαρυτικά φαινόμενα θα εκφράζονται στη βάση της δομής του χωροχρόνου (αρχή της ισοδυναμίας) και η δομή του χωροχρόνου θα επηρεάζεται από την ύλη που βρίσκεται στο χωροχρόνο (αρχή του Μαχ).

H επιτυχία του σ’ αυτήν την αναζήτηση είναι ίσως το μεγαλύτερο επίτευγμα που έχει σημειωθεί ως τώρα στη θεωρητική φυσική. Παρότι κάποιες από τις ιδέες του Μαχ αντανακλώνται στη γενική σχετικότητα, αυτό δεν ισχύει για όλες. Στη γενική σχετικότητα μπορεί να πει κανείς ότι η κίνηση της απομακρυσμένης ύλης επηρεάζει κάποιες τοπικές αδρανειακές ιδιότητες, αλλά δεν τις καθορίζει πλήρως. Ειδικότερα, η περιστροφή μπορεί πάντα να προσδιοριστεί τοπικά, ακόμα και απουσία απομακρυσμένης ύλης.

Η Γενική Σχετικότητα

Η μετατόπιση φ της θέσης ενός αστέρα όπως φαίνεται στον γήινο παρατηρητή εξαιτίας της παρμόρφωσης του χωροχρόνου από τον Ήλιο

O Αϊνστάιν διερωτήθηκε τι θα σήμαινε να ισχύει μια ισοδυναμία μεταξύ επιταχυνόμενων παρατηρητών.  Και είχε την ακόλουθη εξαιρετική ιδέα: Να ταυτίσει τα σώματα που πέφτουν ελεύθερα σε ένα βαρυτικό πεδίο με τους αδρανειακούς παρατηρητές της ειδικής σχετικότητας.

Το ερώτημα αυτό τον οδήγησε σε μια μοναχική πορεία δεκαετούς περίπου σκληρής εργασίας, η οποία τον έφερε από την ειδική σχετικότητα στην καταπληκτική θεωρία που πεζά ονομάζεται γενική σχετικότητα και στην οποία οι έννοιες του χώρου, του χρόνου και της βαρύτητας είναι άρρηκτα συνδεδεμένες.

Το φαινόμενο της βαρύτητας αποτελεί άμεση εκδήλωση της καμπυλότητας του χωροχρόνου. H ενέργεια και η ορμή καμπυλώνουν τον χωρόχρονο, και η καμπυλότητα του χωροχρόνου επηρεάζει την κίνηση της ύλης και της ακτινοβολίας.

O Αϊνστάιν «απελευθέρωσε» τον χωρόχρονο από τον ρόλο του ως άκαμπτου πεδίου στο οποίο εκτυλίσσεται η φυσική. Τον μετέτρεψε από παθητικό θεατή σε δραστήριο παίκτη, που και ο ίδιος παίρνει μέρος στις δυναμικές φυσικές διεργασίες.

H γενική σχετικότητα εξήγησε πολλά παρατηρούμενα γεγονότα τα οποία αδυνατούσε να τα εξηγήσει η θεωρία του Νεύτωνα, προέβλεψε συγκλονιστικά φαινόμενα όπως οι μαύρες τρύπες και, το σπουδαιότερο, άνοιξε την πόρτα σε μια εντελώς νέα, δυναμική προοπτική για το Σύμπαν μας.

Όλοι μας έχουμε την εμπειρία του να στεκόμαστε σε έναν ανελκυστήρα ο οποίος επιταχύνεται προς τα πάνω ή προς τα κάτω. Καταλαβαίνουμε πότε επιταχυνόμαστε προς τα πάνω επειδή αισθανόμαστε βαρύτεροι. Όταν επιταχυνόμαστε προς τα κάτω, αντίθετα, αισθανόμαστε ελαφρότεροι. Φανταστείτε μάλιστα ότι κάποιος κόβει τα καλώδια ανάρτησης, έτσι ώστε ο ανελκυστήρας να εκτελεί ελεύθερη πτώση. Μέσα στην καμπίνα, τώρα, τα πάντα θα είναι «αβαρή»: αν αφήσουμε κάτι από το χέρι μας, αυτό δεν θα μας προσπεράσει για να πέσει στο δάπεδο· απλώς θα παραμένει «μετέωρο» μπροστά μας, κινούμενο μαζί μας προς το δάπεδο.

Από τις παρατηρήσεις αυτές μπορούμε να συμπεράνουμε ότι μια θεωρία σχετικότητας για επιταχυνόμενους παρατηρητές θα πρέπει να περιλαμβάνει πλευρές της βαρύτητας.

O παρατηρητής που πέφτει ελεύθερα θα παίζει έναν μοναδικό ρόλο, καθότι είναι αβαρής* για αυτόν δεν θα υφίσταται βαρύτητα. O Αϊνστάιν ανακάλυψε τον ακρογωνιαίο λίθο της γενικής σχετικότητας το 1907 διατυπώνοντας την αρχή της ισοδυναμίας, συμφωνά με την οποία οι αληθινές δυνάμεις βαρύτητας δεν είναι δυνατόν να διακρίνονται από τις φαινομενικές δυνάμεις αδράνειας.

Δηλαδή, η βαρυτική μάζα ενός σώματος (που εμφανίζεται στη βαρυτική εξίσωση του Νεύτωνα) ταυτίζεται με την αδρανειακή μάζα του (στον περίφημο τύπο του Νεύτωνα F = ma). Στο παρελθόν αυτό αποτελούσε μια φαινομενολογική βεβαίωση, όχι όμως λογική αναγκαιότητα ή θεμελιώδη αρχή.

Υπάρχει ακόμη μία παρατήρηση η οποία πρέπει να γίνει σε σχέση με τους επιταχυνόμενους παρατηρητές: φανταστείτε μια φωτεινή ακτίνα. Εξ ορισμού, αυτή διαγράφει ευθύγραμμη τροχιά μεταξύ δύο σημείων, διότι ο βραχύτερος δρόμος για να φτάσει από το ένα σημείο στο άλλο είναι η ευθεία γραμμή.

Ωστόσο, αν περιγράψουμε αυτή τη γραμμή στο σύστημα αναφοράς ενός παρατηρητή που κινείται με σταθερή επιτάχυνση, τότε η φωτεινή ακτίνα θα διαγράφει μια παραβολή (μια καμπύλη σταθερής καμπυλότητας), και η καμπυλότητα θα ισούται με τη βαρυτική επιτάχυνση — δηλαδή, με το βαρυτικό πεδίο. H ελάχιστη διαδρομή θα είναι μια καμπύλη γραμμή, και αυτό αποτελεί την «υπογραφή» ενός χώρου που είναι ο ίδιος καμπυλωμένος.

Έτσι, οι ανακαλύψεις του Αϊνστάιν ισοδυναμούσαν με μια σχέση μεταξύ επιτάχυνσης και βαρύτητας, από τη μια, και μεταξύ επιτάχυνσης και καμπυλωμένου χώρου, από την άλλη, έτσι ώστε η ταύτιση της βαρύτητας και της καμπυλότητας του χωροχρόνου γινόταν αναπόφευκτη.

Για να φανταστούμε τι εστί καμπυλωμένος χώρος, ίσως θα βοηθούσε να κατεβούμε από τις τρεις διαστάσεις στις δύο. Ας συγκρίνουμε την επιφάνεια ενός επιπέδου με την καμπυλωμένη επιφάνεια μιας σφαίρας. H δεύτερη είναι στην πραγματικότητα μια επιφάνεια σταθερής καμπυλότητας, δεδομένου ότι η επιφάνεια καμπυλώνεται με τον ίδιο τρόπο για όλα τα σημεία και σε όλες τις διευθύνσεις.

Σε μια σφαίρα, η ελάχιστη διαδρομή μεταξύ δύο σημείων είναι πράγματι καμπύλη – τμήμα ενός μέγιστου κύκλου.

H ύλη παράγει γύρω της βαρυτικό πεδίο, γεγονός από το οποίο ο Αϊνστάιν συμπέρανε ότι κάθε μάζα θα έπρεπε να καμπυλώνει το χωρόχρονο γύρω της. Σε δύο διαστάσεις, μια μάζα θα παραμόρφωνε τον επίπεδο χώρο σε επίπεδο με ένα βαθούλωμα γύρω από τη μάζα, σαν να επρόκειτο για ένα ελαστικό φύλλο πάνω στο οποίο έχει τοποθετηθεί η μάζα.

Η εξίσωση της Γενικής Σχετικότητας

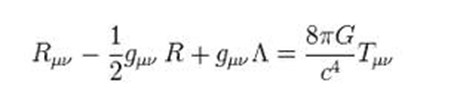
όπου είναι ο τανυστής καμπυλότητας του χώρου Ricci, ο όρος είναι η βαθμωτή καμπυλότητα, ο όρος είναι ο μετρικός τανυστής, το Λ είναι η κοσμολογική σταθερά, το G είναι η βαρυτική σταθερά του Νεύτωνα, C είναι η ταχύτητα του φωτός στο κενό και    ο τανυστής ορμής-ενέργειας.  Οι δύο πρώτοι όροι στην αριστερή πλευρά αναφέρονται σαν ο τανυστής Einstein Gμν.

Όπως και στην ειδική σχετικότητα, η μετρική περιέχει όλες τις πληροφορίες που αφορούν στη χωροχρονική σχέση των γεγονότων. Περιγράφει πλήρως το βαρυτικό πεδίο προσδιορίζοντας, μέσω των χρονοειδών γεωδαισιακών, την κίνηση όλων των παρατηρητών σε ελεύθερη πτώση. Κατά συνέπεια, η περιγραφή της βαρύτητας είναι αναπόσπαστα συνδεδεμένη με τις ιδιότητες του χωροχρόνου, καθώς και τα δύο περιγράφονται από μία και μοναδική ποσότητα, τη χωροχρονική μετρική. To βαρυτικό πεδίο είναι στην ουσία η καμπυλότητα της χωροχρονικής γεωμετρίας. Ένα δηλαδή πλαίσιο της γενικής σχετικότητας είναι ότι το βαρυτικό πεδίο περιγράφεται από την καμπύλη γεωμετρία του χωροχρόνου.

Για να ολοκληρωθεί όμως η θεωρία, απαιτείται ακόμα ένας κανόνας ο οποίος να προσδιορίζει ποιά χωροχρονική γεωμετρία (δηλαδή ποιό βαρυτικό πεδίο) σχετίζεται με κάθε συγκεκριμένη κατανομή ύλης. O κανόνας που έδωσε ο Αϊνστάιν πήρε τη μορφή της παραπάνω εξίσωσης, η οποία στην ουσία της λέει:

«καμπυλότητα του χωροχρόνου» = «πυκνότητα ενέργειας της ύλης»

Με αυτόν τον τρόπο ο Αϊνστάιν ολοκλήρωσε μία πραγματικά εντυπωσιακή και όμορφη θεωρία της βαρύτητας, τα αποτελέσματα της βαρύτητας σχετίζονται πλήρως με τη δομή του χωροχρόνου και όπου, σύμφωνα με κάποιες από τις ιδέες του Μαχ, η δομή του χωροχρόνου προκύπτει μέσω της εξίσωσης του Αϊνστάιν από την κατανομή της ύλης στο χωροχρόνο.

H παραπάνω περιγραφή της εξίσωσης του Αϊνστάιν είναι κάπως υπεραπλουστευμένη και γι’ αυτόν το λόγο πρέπει να προσθέσουμε μερικά σχόλια. Πρώτον, το αριστερό μέλος της εξίσωσης δεν περιέχει όλη την καμπυλότητα του χωροχρόνου, αλλά μόνο ένα μέρος της. Αυτό σημαίνει ότι έξω από μία κατανομή ύλης (όπου το δεξιό μέλος της εξίσωσης του Αϊνστάιν μηδενίζεται) ο χωροχρόνος θα είναι γενικά καμπύλος, δηλαδή θα υπάρχει βαρυτικό πεδίο. Επίσης, μπορεί να υπάρχει βαρυτική ακτινοβολία, δηλαδή μεταβολές της καμπυλότητας που διαδίδονται στο χωροχρόνο υπό μορφή κυμάτων. Δεύτερον, το δεξιό μέλος περιέχει συνεισφορές κι από άλλες ιδιότητες της ύλης, πέρα από την πυκνότητα της ενέργειας. Ειδικότερα, η ροή της ενέργειας και η πίεση συνεισφέρουν κι αυτές στην καμπυλότητα του χωροχρόνου.

Αν δεν υπάρχει καθόλου ύλη, το δεξιό μέλος της εξίσωσης του Αϊνστάιν μηδενίζεται και μία καθ’ όλα αποδεκτή λύση είναι η επίπεδη χωροχρονική γεωμετρία της ειδικής σχετικότητας. Υπάρχουν ωστόσο κι άλλες λύσεις, οι οποίες περιγράφουν πιθανά βαρυτικά πεδία στο εξωτερικό σωμάτων, βαρυτικά κύματα κ.λπ. Υπό αυτήν την έννοια, η γενική σχετικότητα εμπεριέχει την ειδική σχετικότητα σαν ειδική περίπτωση.

Στην περιγραφή μας για τη γενική σχετικότητα, δεχτήκαμε ως βασική υπόθεση το ότι σώματα σε ελεύθερη πτώση ακολουθούν γεωδαισιακές της χωροχρονικής μετρικής. Ωστόσο αποδεικνύεται (η απόδειξη δόθηκε περίπου δέκα χρόνια μετά τη διατύπωση της γενικής σχετικότητας) ότι η εξίσωση του Αϊνστάιν από μόνη της αρκεί για να προσδιορίσει την κίνηση της ύλης στο χωροχρόνο. H «υπόθεση των γεωδαισιακών» αποτελεί, λοιπόν, συνέπεια της εξίσωσης Αϊνστάιν και όχι αυτόνομη υπόθεση.

Τέλος, σημειώνουμε ότι στην πράξη είναι πολύ δύσκολο να βρει κανείς ακριβείς λύσεις των εξισώσεων Αϊνστάιν. Ευτυχώς, πολλές λύσεις με μεγάλο φυσικό ενδιαφέρον είναι γνωστές (όπως αυτές που περιγράφουν μελανές οπές) και οι ιδιότητες των αντίστοιχων χωροχρόνων έχουν μελετηθεί λεπτομερώς. Ωστόσο, η άγνοια των γενικών λύσεων της εξίσωσης Αϊνστάιν εμποδίζει τον προσδιορισμό των γενικότερων δυνατών χωροχρονικών δομών που είναι συμβατές με τη γενική σχετικότητα.

Περιγραφή της εξίσωσης

Η εξίσωση του Αϊνστάιν εκφράζουν ακριβώς αυτά που μόλις περιγράψαμε. Στο αριστερό μέλος τα πεδία (x, t) παριστούν τις συνιστώσες της καμπυλότητας στις διάφορες διευθύνσεις του χωροχρόνου σε κάθε χωροχρονικό σημείο, ενώ στο δεξιό μέλος βρίσκουμε ένα πεδίο με πολλές συνιστώσες (x, t) το οποίο περιγράφει την πυκνότητα ενέργειας και ορμής στον χωρόχρονο.

Οι δείκτες μ και ν είναι χωροχρονικοί δείκτες, λαμβάνουν τις τέσσερις τιμές 0, 1, 2 και 3 — όπου το μηδέν αναφέρεται στη χρονική συνιστώσα. Έτσι, στο αριστερό μέλος εμφανίζεται όλη η πληροφορία για τη γεωμετρία του χωροχρόνου, ενώ στο δεξιό μέλος δίνεται όλη η πληροφορία σχετικά με την κατανομή της ύλης και της ακτινοβολίας.

O όρος που περιέχει τη λεγόμενη «κοσμολογική σταθερά» Λ θα μπορούσε να έχει γραφεί είτε στο αριστερό είτε στο δεξιό μέλος, ανάλογα με το πώς ερμηνεύουμε τη Λ. Από τη μια, η ύλη και η ενέργεια καθορίζουν πώς καμπυλώνεται ο χωρόχρονος, ενώ, από την άλλη, η καμπυλότητα του χωροχρόνου λειτουργεί ως βαρυτική δύναμη και επομένως καθορίζει πώς κινούνται τόσο τα σωματίδια όσο και το φως.

Το κρίσιμο σημείο δεν έγκειται μόνο στο ότι ο χωρόχρονος είναι καμπυλωμένος αλλά — το σπουδαιότερο — στο ότι είναι δυναμικός. Αυτό σημαίνει ότι ο χωρόχρονος δεν αποτελεί απλώς έναν μαθηματικό στίβο όπου διεξάγεται η φυσική, αλλά ότι ο ίδιος λαμβάνει δραστήρια μέρος στο παιχνίδι, συμμετέχοντας σε δυναμικές διεργασίες ακριβώς όπως και οι λοιποί φυσικοί βαθμοί ελευθερίας.

Υπάρχει μία ακόμη αναλογία η οποία ίσως μας βοηθήσει να συλλάβουμε τη ριζική τροπή στην εννοιολογική μας κατανόηση της βαρύτητας που συνεπάγονται οι εξισώσεις του Αϊνστάιν, τούτη τη φορά όχι υπό το μανδύα ενός καμπυλωμένου χωροχρόνου. Στον ηλεκτρομαγνητισμό ο νόμος που προσδιορίζει την ελκτική ή απωστική δύναμη μεταξύ δύο σημειακών φορτίων παρουσιάζει μεγάλη ομοιότητα με τον νόμο της βαρυτικής έλξης μεταξύ δύο σημειακών μαζών, όπως τον διατύπωσε ο Νεύτων.

Ξέρουμε ότι στις εξισώσεις του Maxwell βλέπουμε την ανάδυση του ηλεκτρικού και του μαγνητικού πεδίου, όχι απλώς ως μαθηματικών κατασκευών για τον υπολογισμό των δυνάμεων που αναπτύσσονται μεταξύ φορτίων, αλλά ως ανεξάρτητων φυσικών βαθμών ελευθερίας που ικανοποιούν τις εξισώσεις αυτές. Αυτές οι εξισώσεις έχουν λύσεις που αντιστοιχούν σε ηλεκτρομαγνητικά κύματα διαδιδόμενα διαμέσου του κενού — εξ ορισμού, με την ταχύτητα του φωτός. Έτσι επιλύθηκε ο παρακάτω γρίφος που επί μακρόν ταλάνιζε τους επιστήμονες.

Φανταστείτε ότι κάπου θέτουμε σε κίνηση ένα φορτίο, οπότε περιμένουμε το πεδίο να μεταβληθεί, αυτή δε η μεταβολή του πεδίου να αναγκάσει κάποιο άλλο πάρα πολύ απομακρυσμένο φορτίο να τεθεί σε κίνηση. Σύμφωνα με τον παλιό νόμο της ηλεκτρικής δύναμης, η δύναμη μεταδίδεται ακαριαία. Αν, ωστόσο, μελετήσετε τις εξισώσεις Maxwell, θα διαπιστώσετε ότι η μεταβολή του πεδίου δεν διαδίδεται παρά με την ταχύτητα του φωτός — διασώζοντας φυσικά την ιερή έννοια της αιτιότητας.

O Αϊνστάιν, εν προκειμένω, κατανοούσε άριστα ότι, με τον νευτώνειο νόμο της βαρύτητας, η ίδια η «ακαριαία δράση εξ αποστάσεως» θα προκαλούσε ένα εννοιολογικό πρόβλημα. Με άλλα λόγια, με την ειδική σχετικότητα ο Αϊνστάιν είχε λύσει την αντίθεση ανάμεσα στις εξισώσεις Maxwell και τις δυναμικές εξισώσεις του Νεύτωνα, όμως η αντίθεση με το νόμο της βαρυτικής δύναμης παρέμενε σε εκείνη τη φάση ακόμη ανεπίλυτη.

O Αϊνστάιν ήξερε τι έπρεπε να αναζητήσει: ένα σύνολο εξισώσεων για το βαρυτικό πεδίο, οι οποίες θα έπαιζαν τον ίδιο ρόλο με εκείνες του Maxwell στον ηλεκτρομαγνητισμό. Οι εξισώσεις για το βαρυτικό πεδίο θα έπρεπε να είναι παρόμοιες με τις εξισώσεις Maxwell αλλά βεβαίως όχι ακριβώς ίδιες — τουλάχιστον εξαιτίας του ότι η βαρυτική δύναμη μεταξύ μαζών λειτουργεί πάντοτε ελκτικά. Και αυτό ακριβώς βρήκε. Το γεγονός ότι οι εξισώσεις του επέτρεπαν ταυτόχρονα μια γεωμετρική ερμηνεία που συνεπαγόταν την καμπυλότητα του χώρου και του χρόνου στάθηκε από αυτή την άποψη ένα απροσδόκητο αλλά υπέροχο δώρο.

H θεωρία της βαρύτητας του Αϊνστάιν συγκαταλέγεται μεταξύ των πλέον καλαίσθητων επιτευγμάτων της θεωρητικής φυσικής. Ενσάρκωσε ένα σπουδαίο εννοιολογικό σημείο καμπής και έδωσε αρκετές αξιοσημείωτες προβλέψεις, προχωρώντας πολύ πέρα από τη θεωρία του Νεύτωνα.