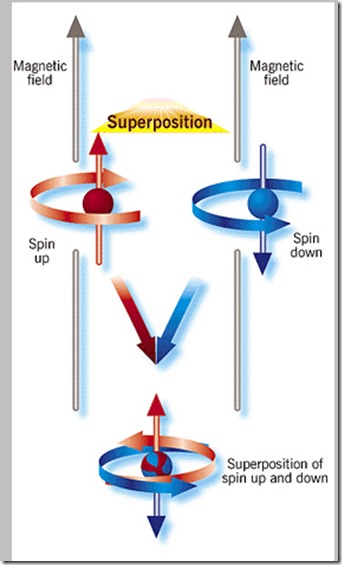
Σύμφωνα με την κβαντομηχανική, και ειδικότερα σύμφωνα με την εικόνα του Schrodinger, κάθε σύστημα περιγράφεται από μια κυματοσυνάρτηση η οποία είναι συνάρτηση της θέσης των σωματιδίων του συστήματος και του χρόνου. Το τετράγωνο αυτής της συνάρτησης εκφράζει την πιθανότητα να βρεθεί το σύστημά μας στις συγκεκριμένες θέσεις την συγκεκριμένη χρονική στιγμή.
Η εξέλιξη της κυματοσυνάρτησης αυτής με το χρόνο -η οποία περιγράφεται από μια διαφορική εξίσωση, την εξίσωση του Schrodinger – είναι ομαλή και συνεχής. Μια τέτοια εξέλιξη στα μαθηματικά λέγεται μοναδιαία (unitary) και έχει πολλές ενδιαφέρουσες ιδιότητες.
Μια από τις σημαντικότερες ιδιότητες της εξίσωσης του Schrodinger και της κυματοσυνάρτησης είναι ότι κάθε επαλληλία διαφορετικών συναρτήσεων που αποτελούν λύσεις της εξίσωσης Schrodinger για ένα συγκεκριμένο σύστημα, θα είναι επίσης λύση που θα παριστάνει την εξέλιξη του συστήματος.
Με άλλα λόγια ένα κβαντικό σύστημα που μπορεί να βρίσκεται ξεχωριστά σε δύο διαφορετικές καταστάσεις, μπορεί να βρίσκεται και σε ένα γραμμικό συνδυασμό αυτών των καταστάσεων.
Αυτή είναι η κβαντική υπέρθεση των καταστάσεων. Και μάλιστα, αν αρχικά το σύστημά μας βρίσκεται σε μια τέτοια υπέρθεση, ο μοναδιαίος τρόπος της εξέλιξής του υπαγορεύει ότι αν δεν μεσολαβήσει κάποια αλληλεπίδραση του συστήματος με το περιβάλλον, το σύστημα θα εξακολουθήσει να βρίσκεται σ’ αυτή την υπέρθεση.
Ας εξετάσουμε ένα νοητό παράδειγμα που εμφανίζονται τα παραπάνω.
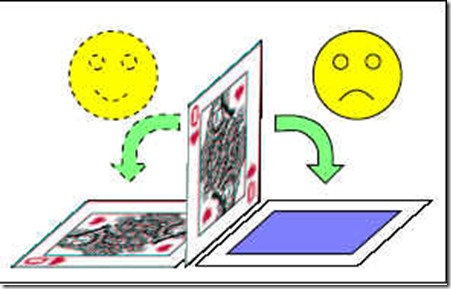
Σύμφωνα με την κβαντομηχανική ένα τραπουλόχαρτο που ισορροπεί στην κόψη του βρίσκεται σε μια υπέρθεση δύο καταστάσεων. Μιας που φαίνεται η φιγούρα του τραπουλόχαρτου και μιας που είναι η πίσω όψη του (με μπλε χρώμα στην εικόνα.)
Σύμφωνα πάλι με την κβαντομηχανική, όταν το τραπουλόχαρτο πέσει, ο μοναδιαίος τρόπος εξέλιξης της κυματοσυνάρτησης προβλέπει ότι θα πέσει και με τις δύο όψεις συγχρόνως αφού η υπέρθεση πρέπει να διατηρείται.
Η πράξη της παρατήρησης όμως του τραπουλόχαρτου από ένα παρατηρητή, πυροδοτεί μια απότομη μεταβολή στην κυματοσυνάρτηση και αυτή καταρρέει όπως λέμε σε μια εκ των δύο καταστάσεων που την αποτελούν.
Ο παρατηρητής βλέπει λοιπόν μια εκ των δύο κλασσικών καταστάσεων (η φιγούρα στην επάνω όψη ή η φιγούρα στην κάτω όψη) και από κει και ύστερα η κλασσική αυτή κατάσταση επιζεί.
Υποτίθεται ότι η φύση κατά τελείως τυχαίο τρόπο αποφάσισε σε ποια εκ των δύο κλασικών καταστάσεων θα καταρρεύσει. Οι πιθανότητες γι αυτό καθορίζονται από τους συντελεστές των δύο καταστάσεων όταν αυτές σχηματίζουν την υπέρθεση.
Αν και η μέθοδος αυτή δουλεύει μια χαρά για τους υπολογισμούς μας, εν τούτοις παραμένει ένα μυστήριο το πότε και πως γίνεται η κατάρρευση της κυματοσυνάρτησης.
Στα μέσα της δεκαετίας του 1950, ένας σπουδαστής στο Princeton, o Hugh Everett III αποφάσισε να καταπιαστεί με το θέμα της κατάρρευσης της κυματοσυνάρτησης στη διδακτορική του διατριβή.
Ο Everett προχώρησε την ιδέα της κβαντομηχανικής στα άκρα, θέτοντας την εξής ερώτηση: Τι θα συνέβαινε αν η χρονική εξέλιξη ολόκληρου του Σύμπαντος ήταν πάντα μοναδιαία; Αν τελικά η κβαντομηχανική είναι σωστή και για το Σύμπαν θα πρέπει αυτό να περιγράφεται από μια κυματοσυνάρτηση (όσο περίπλοκη κι αν είναι αυτή.)
Στο σενάριο του Everett αυτή η κυματοσυνάρτηση θα εξελίσσεται κατά ντετερμινιστικό τρόπο, αφού δεν υπάρχει τίποτα έξω από το σύμπαν για να τη διαταράξει, κι έτσι δεν υπάρχει δυνατότητα για να καταρρεύσει.
Στη θεώρηση του Everett το κβαντικό τραπουλόχαρτο θα βρίσκεται και με τις δύο όψεις του συγχρόνως. Επιπλέον, ένας παρατηρητής που το βλέπει εισάγει ακόμα μια υπέρθεση δύο διανοητικών καταστάσεων όπου κάθε μια αντιστοιχεί και σε ένα από τα δύο πιθανά αποτελέσματα της του, την διαφορετική εικόνα που αντιλαμβάνεται.
Αν είχατε στοιχηματίσει χρήματα ότι θα έλθει η όψη της φιγούρας, θα καταλήγατε σε μια υπέρθεση να χαμογελάτε και να στενοχωρείστε, όπως δείχνει εύγλωττα και η παραπάνω εικόνα.
Οι παρατηρητές σε ένα τέτοιο τρελό αλλά ντετερμινιστικό κόσμο, κάθε φορά που θα εκτελούσαν μια παρατήρηση θα έμπαιναν σε ένα από τα πιθανά σενάρια αφού και οι ίδιοι θα ήταν μέρος του μεγάλου συστήματος, αλλά και τα υπόλοιπα θα εξακολουθούσαν να εξελίσσονται.
Η θεώρηση αυτή του Everett έμεινε γνωστή ως “ερμηνεία των πολλών κόσμων” της κβαντομηχανικής, ή μάλλον των “πολλών συνειδήσεων”, γιατί καθεμιά από τις υπερτιθέμενες διανοητικές καταστάσεις αντιλαμβάνεται το δικό της κόσμο. Η θεώρηση αυτή δεν χρειάζεται μεν πια το αξίωμα της κατάρρευσης, αλλά το αντίτιμο που πληρώνει είναι ότι αυτές οι παράλληλες αντιλήψεις του κόσμου είναι όλες εξίσου πραγματικές.
Η δουλειά του Everett είχε αφήσει δυο μεγάλα αναπάντητα ερωτηματικά:
Πρώτα απ’ όλα, αν ο κόσμος περιέχει πραγματικά τέτοιες μκρο-υπερθέσεις, γιατί δεν τις αντιλαμβανόμαστε;
Η απάντηση ήρθε στα 1970 από τον Dieter Zeh του πανεπιστημίου της Heidelberg, ο οποίος έδειξε ότι η ίδια η εξίσωση του Schrodinger επιβάλλει κάποιο τύπο λογοκρισίας.
Το φαινόμενο αυτό είναι γνωστό ως αποσυμφωνία ή καταστροφή της υπέρθεσης (decoherence). Η καταστροφή της υπέρθεσης μελετήθηκε διεξοδικά από τους Wojciech Zurek, Zeh και άλλους στις επόμενες δεκαετίες.
Αυτοί βρήκαν ότι οι σύμφωνες κβαντικές υπερθέσεις διαρκούν μόνο όσο παραμένουν “μυστικές” και απομονωμένες από το υπόλοιπο του κόσμου. Το κβαντικό τραπουλόχαρτο του παραδείγματός μας επικοινωνεί με τα μόρια του αέρα, με φωτόνια κλπ, τα οποία εξερευνούν με ποια όψη έχει πέσει, καταστρέφοντας έτσι την υπέρθεση και κάνοντάς την αδύνατη να παρατηρηθεί.
Ο πιο βολικός τρόπος να καταλάβουμε την καταστροφή της υπέρθεσης μαθηματικά είναι να κάνουμε χρήση μιας γενίκευσης της κυματοσυνάρτησης που λέγεται “πίνακας ή μήτρα πυκνότητας πιθανοτήτων” (density matrix).
Για κάθε κυματοσυνάρτηση υπάρχει μια αντίστοιχη τέτοια μήτρα, και μια αντίστοιχη εξίσωση Schrodinger για τις μήτρες αυτές. Για παράδειγμα η μήτρα πυκνότητας για το κβαντικό τραπουλόχαρτο που πέφτει σε υπέρθεση θα μοιάζει κάπως έτσι:
Οι αριθμοί a και b είναι οι πιθανότητες να βρούμε το τραπουλόχαρτο με τη φιγούρα προς τα επάνω ή προς τα κάτω αντίστοιχα, και στην περίπτωσή μας θα ισούνται και τα δύο με 1/2. Πράγματι ένας πίνακας πυκνότητας με τη μορφή:
θα παριστάνει τη γνωστή κλασσική κατάσταση όπου το τραπουλόχαρτο δείχνει είτε την όψη της φιγούρας είτε την αντίθετη όψη, αλλά δεν γνωρίζουμε ποια. Τα μη διαγώνια στοιχεία του πίνακα, τα c στην περίπτωσή μας παριστάνουν τις διαφορές μεταξύ της κβαντικής αβεβαιότητας των υπερθέσεων και της κλασσικής αβεβαιότητας που προέρχεται απλώς από άγνοια.
Ένα αξιοσημείωτο επίτευγμα της θεωρίας καταστροφής της υπέρθεσης είναι ότι εξηγεί πως η αλληλεπίδραση ενός αντικειμένου με το περιβάλλον του μεταβάλλει τα μη διαγώνια στοιχεία του πίνακα σε 0, αντικαθιστώντας έτσι την κβαντική υπέρθεση με απλή κλασσική άγνοια.
Η καταστροφή της κβαντικής υπέρθεσης μας εξηγεί γιατί δεν παρατηρούμε συνήθως κβαντικές υπερθέσεις στον μακροσκοπικό κόσμο γύρω μας.
Δεν είναι ότι η κβαντομηχανική σταματά να ισχύει από κάποιο μαγικό μέγεθος και πάνω, αλλά ότι είναι εξαιρετικά δύσκολο να απομονώσουμε ένα μακροσκοπικό σύστημα από το περιβάλλον του ώστε να εμποδίσουμε την καταστροφή της υπέρθεσης. Αντίθετα τα μικροσκοπικά αντικείμενα απομονώνονται πιο εύκολα και διατηρούν περισσότερο την κβαντική τους συμπεριφορά.
Το δεύτερο αναπάντητο ερώτημα στην εικόνα του Everett ήταν πιο λεπτό αλλά εξίσου σημαντικό: Ποιός φυσικός μηχανισμός επιλέγει τις κλασσικές καταστάσεις – η φιγούρα πάνω ή κάτω στην περίπτωσή μας – ως ειδικές για να προτιμηθούν;
Από μαθηματική σκοπιά κβαντικές καταστάσεις όπως “φιγούρα στην επάνω όψη + φιγούρα στην κάτω όψη” (ας την αποκαλέσουμε “κατάσταση άλφα”) είτε η “φιγούρα στην επάνω όψη – φιγούρα στην κάτω όψη” (ας την αποκαλέσουμε “κατάσταση βήτα”) είναι εξίσου ισχυρές κλασσικές καταστάσεις σαν τις “φιγούρα στην επάνω όψη” , “φιγούρα στην κάτω όψη”.
Έτσι λοιπόν όπως ακριβώς το τραπουλόχαρτό μας που έπεσε στην κατάσταση “άλφα”, και η κυματοσυνάρτηση του κατέρρευσε στην κατάσταση “φιγούρα στην επάνω όψη” ή “φιγούρα στην κάτω όψη”, έτσι θα μπορούσε και ένα τραπουλόχαρτο που βρίσκεται αρχικά στην κατάσταση: “φιγούρα στην επάνω όψη” – η οποία ισούται με (άλφα + βήτα)/2 – να καταρρεύσει στην “άλφα” ή στην “βήτα” κατάσταση.
Γιατί όμως δεν παρατηρούμε ποτέ κάτι τέτοιο;
Η καταστροφή της υπέρθεσης απαντάει και στην ερώτηση αυτή. Οι υπολογισμοί έδειξαν ότι οι κλασσικές καταστάσεις θα μπορούσαν να οριστούν και να προσδιοριστούν, ως εκείνες οι καταστάσεις που είναι πιο ανθεκτικές απέναντι στην καταστροφή της υπέρθεσης.
Με άλλα λόγια η καταστροφή της υπέρθεσης κάνει κάτι παραπάνω από το να μετατρέπει σε 0 τα μη διαγώνια στοιχεία του πίνακα πυκνότητας πιθανότητας. Αν λοιπόν οι καταστάσεις “άλφα” και “βήτα” του τραπουλόχαρτου επιλέγονταν ως θεμελιώδεις βασικές καταστάσεις ο πίνακας πυκνότητας για το πεσμένο τραπουλόχαρτο θα ήταν διαγώνιος και με την απλή μορφή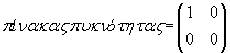
αφού το χαρτί θα ήταν σίγουρα στην κατάσταση “άλφα.” Όμως η καταστροφή της υπέρθεσης θα άλλαζε σχεδόν στιγμιαία την κατάσταση αυτή σε:
Έτσι αν μπορούσαμε να μετρήσουμε αν το τραπουλόχαρτο ήταν στην “άλφα” ή “βήτα” κατάσταση, θα παίρναμε ένα τυχαίο αποτέλεσμα. Αντίθετα αν βάζαμε το χαρτί στην κατάσταση “φιγούρα προς τα επάνω” θα παρέμενε σ’ αυτή χωρίς να υφίσταται καταστροφή υπέρθεσης.
Η καταστροφή της υπέρθεσης αποτελεί λοιπόν αυτό που ο Zurek ονόμασε “κόσκινο προγνωσιμότητας”, επιλέγει δηλαδή εκείνες τις καταστάσεις που εμφανίζουν κάποια σταθερότητα και η χρήση των οποίων δίνει στη φυσική κάποια προγνωστική δύναμη.
