Το μεγαλύτερο λάθος του Αϊνστάιν, όπως ο ίδιος παραδέχθηκε σε μια συνομιλία που είχε με τον George Gamow, ήταν η εισαγωγή κατά το 1917 μιας κοσμολογικής σταθεράς Λ στις εξισώσεις της γενικής σχετικότητας. Ο λόγος που το έκανε ήταν γιατί την εποχή εκείνη οι φυσικοί πίστευαν ότι το σύμπαν ήταν στατικό, ενώ οι εξισώσεις οδηγούσαν τον Αϊνστάιν σε ένα μεταβαλλόμενο σύμπαν.
Τα λάθη που γίνονται από τους κορυφαίους επιστήμονες βοηθούν εν συνεχεία άλλους να κατανοήσουν τι συνέβαινε στην εποχή εκείνη, πολύ περισσότερο από τις επιτυχίες τους. Και όταν το 1917 τελείωσε με τη Γενική Σχετικότητα ο Αϊνστάιν προσπάθησε να κάνει μια εκτίμηση της χωροχρονικής δομής ολόκληρου του σύμπαντος. Τότε ήταν που αντιμετώπισε το μεγάλο πρόβλημα. Ο Αϊνστάιν υπέθετε ότι όταν υπολογιστεί η μέση πυκνότητα, το σύμπαν είναι ομοιόμορφο και ουσιαστικά στατικό αλλά οι εξισώσεις της γενικής σχετικότητας δεν φάνηκαν να επιτρέπουν μια λύση για ένα σύμπαν ανεξάρτητο του χρόνου με μία ομοιόμορφη κατανομή της ύλης. Έτσι τροποποίησε τις εξισώσεις πεδίου του Alexander Friedmann, βάζοντας ένα νέο όρο σε αυτές που περιλάμβανε αυτό που ονόμασε κοσμολογική σταθερά Λ.
Επίσης, είχε διαπιστώσει ότι στον καμπυλωμένο χωροχρόνο θα μπορούσε να αποθηκευτεί βαρυτική ενέργεια. Αυτό ακριβώς εκφράζει η κοσμολογική σταθερά Λ: την ενεργειακή πυκνότητα του κενού χώρου. Η γνωστή σε μας νευτώνεια δύναμη της βαρύτητας είναι πάντα ελκτική. Αντίθετα, μια θετική κοσμολογική σταθερά δημιουργεί απωστικό πεδίο βαρύτητας. Αν όμως υπάρχει στο σύμπαν μόνο η ελκτική δύναμη της βαρύτητας τότε το σύμπαν θα κατέρρεε και δεν θα μπορούσε να ήταν στατικό, όπως πίστευαν μέχρι τότε. Γι αυτό και ο Einstein σκέφτηκε ότι η άπωση που προερχόταν από την κοσμολογική σταθερά θα μπορούσε να ισορροπήσει το σύμπαν.
Όταν ανακαλύφθηκε αργότερα ότι το σύμπαν δεν είναι στατικό αλλά διαστελλόμενο, ο Αϊνστάιν μετέτρεψε την αρχική θεωρία του. Μπορεί, επίσης, να τον είχε ενοχλήσει το γεγονός ότι δεν είχε προβλέψει την διαστολή του σύμπαντος.
Όμως, πρώτον το λάθος του δικαιολογείται αν σκεφθούμε ότι οι θεωρητικοί αντιλαμβάνονται το σύμπαν όπως αυτό παρουσιάζεται στους παρατηρητές. Οι σχετικά χαμηλές παρατηρηθείσες ταχύτητες των αστεριών την εποχή εκείνη (1917), ανάγκαζαν τους επιστήμονες να υποθέτουν ότι το σύμπαν είναι σχεδόν σίγουρα στατικό. Κατά συνέπεια όταν ο Willem de Sitter (1872-1934) πρότεινε μια εναλλακτική λύση στις εξισώσεις του Αϊνστάιν το 1917, αναγκάστηκε να χρησιμοποιήσει συντεταγμένες για τις οποίες ο μετρικός τανυστής ήταν ανεξάρτητος του χρόνου. Πάντως, η φυσική έννοια αυτών των συντεταγμένων δεν ήταν καθαρή, και όταν αναγνωρίστηκε ότι η εναλλακτική κοσμολογία του de Sitter δεν ήταν στατική – ότι δηλαδή τα σωματίδια της ύλης στο μοντέλο του επιταχύνονται μακριά το ένα από το άλλο — αυτό θεωρήθηκε ένα μειονέκτημα της θεωρίας του.
Κατά δεύτερον, το λάθος αυτό ήταν δικαιολογημένο αν σκεφτούμε ότι ο Αϊνστάιν δεν γνώριζε την εποχή εκείνη ένα αποτέλεσμα των παρατηρήσεων του αστρονόμου Vesto Melvin Slipher.
Ο Slipher (1875-1969) παρατηρώντας τα φάσματα των σπειροειδών νεφελωμάτων τη δεκαετία του 1910, είχε βρει μια παραπάνω ερυθρή μετατόπιση από όση ήταν δικαιολογημένη σε μια διαστολή μόνο από την επίδραση Doppler, αλλά κανένας δεν ήξερε τότε τι ήταν τα σπειροειδή νεφελώματα. Μέχρι που ο Edwin Hubble (1889-1953) βρήκε μια εξασθένιση στο φως των μεταβλητών Κηφείδων στο νεφέλωμα της Ανδρομέδας το 1923 και έτσι έγινε σαφές ότι τα σπειροειδή νεφελώματα ήταν απόμακροι γαλαξίες – σμήνη αστεριών πολύ μακριά έξω από το Γαλαξία μας. Μέχρι το 1917 ο Einstein δεν είχε ακούσει ποτέ για την ερυθρή μετατόπιση που βρήκε ο Slipher, αλλά εν πάση περιπτώσει ήξερε πολύ καλά τουλάχιστον ένα πράγμα που θα μπορούσε να παραγάγει επίσης μια ερυθρή μετατόπιση των φασματικών γραμμών: Κι αυτό ήταν ένα βαρυτικό πεδίο.
Πρέπει να αναγνωριστεί εδώ ότι ο Arthur Eddington (1882-1944), που είχε μάθει για τη γενική σχετικότητα κατά τη διάρκεια του Α! παγκόσμιου πολέμου από τον de Sitter, ερμήνευσε το 1923 την ερυθρή μετατόπιση του Slipher ότι οφειλόταν στη διαστολή του σύμπαντος στο μοντέλο de Sitter. Εντούτοις, η διαστολή του σύμπαντος δεν έγινε αποδεκτή πάρα μόνο όταν ο Hubble ανάγγειλε το 1929 — και στην πράξη παρουσιάστηκε το 1931 — ότι οι ερυθρές μετατοπίσεις των απόμακρων γαλαξιών αυξάνονται αναλογικά προς την απόστασή τους, όπως θα αναμενόταν για μια ομοιόμορφη διαστολή του σύμπαντος.
Μόνο τότε δόθηκε η προσοχή που άξιζε στα μοντέλα ενός διαστελλόμενου σύμπαντος που εισήχθηκαν το 1922 από τον Alexander Friedmann (1888-1925), στα οποία δεν χρειάζεται να υπάρχει καμία κοσμολογική σταθερά. Τότε ήταν μια εποχή που οι Einstein, Willem de Sitter και Georges Lemaitre δούλευαν τις εξισώσεις για την περιγραφή του σύμπαντος.
Η εξίσωση του Friedmann
Ο Friedmann ανέπτυξε κι αυτός μια δυναμική εξίσωση για το διαστελλόμενο σύμπαν ως μια σχετικιστική εξίσωση στα πλαίσια της Γενικής Σχετικότητας. Όμως εδώ η περιγραφή της θα περιοριστεί σε μια απλουστευμένη, μη-σχετικιστική έκδοση.
Παρακάτω φαίνεται μια κατάλληλη μορφή της εξίσωσης του Friedmann, με την οποία σχετίζεται ο χρόνος διαστολής και η θερμοκρασία για ένα μοντέλο της Μεγάλης Έκρηξης του σύμπαντος
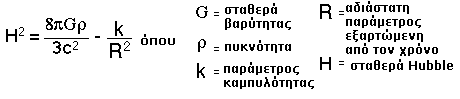
Εκτός από την πυκνότητα και τη σταθερά βαρύτητας G, η εξίσωση περιέχει τη παράμετρο Hubble H, μια βαθμωτή (αριθμητική) παράμετρο R, και έναν παράγοντα Κ που ονομάζεται παράμετρος κυρτότητας. Η παράμετρος κυρτότητας δείχνει εάν το σύμπαν είναι ανοικτό ή κλειστό.
Ο Einstein είχε αρχικά προσθέσει κι έναν άλλο όρο, τη διάσημη κοσμολογική σταθερά Λ, με την οποία η εξίσωση αυτή θα περιέγραφε ένα στατικό Σύμπαν.
Η παραπάνω εξίσωση του Friedmann έχει μια παράμετρο κυρτότητας k, που είναι ενδεικτική του ρυθμού διαστολής και εάν ο ρυθμός διαστολής αυξάνεται ή μειώνεται. Έτσι, αν η παράμετρος k=0 τότε η πυκνότητα είναι ίση με μια κρίσιμη τιμή στην οποία το σύμπαν θα διαστέλλεται για πάντα αλλά με ένα μειούμενο ρυθμό. Αυτό αναφέρεται συχνά ως μοντέλο σύμπαντος των Einstein-De Sitter σε αναγνώριση της εργασίας τους για τη διαμόρφωση του. Η τιμή της παραμέτρου k=0 μπορεί να χρησιμοποιηθεί για να εκφράσει την κρίσιμη πυκνότητα με βάση τη σημερινή τιμή της παραμέτρου Hubble H.
Για τιμή της k>0 η πυκνότητα της ύλης είναι αρκετά υψηλή και έτσι η βαρυτική έλξη θα σταματήσει τελικά την διαστολή του σύμπαντος που θα καταρρεύσει προς τα πίσω σε μια “Μεγάλη Σύνθλιψη”. Αυτό το είδος του σύμπαντος περιγράφεται ως ένα Κλειστό Σύμπαν, ή ένα βαρυτικά συνδεδεμένος κόσμος. Για τιμή του Κ<0 το σύμπαν θα διαστέλλεται για πάντα, αφού δεν υπάρχει αρκετή πυκνότητα ύλης για να προκαλέσει τέτοια βαρυτική έλξη, που να σταματήσει την διαστολή.
Ο Einstein πρότεινε μια τροποποίηση στην εξίσωση του Friedmann, που αναφέρεται σε ένα διαστελλόμενο σύμπαν. Πρόσθεσε έναν όρο που τον ονόμασε κοσμολογική σταθερά Λ, και η οποία μορφοποιεί την εξίσωση Friedmann ως εξής:
![]()
Η κοσμολογική σταθερά Λ φαίνεται να εκφράζει μια βαρυτική άπωση ανάλογη της απόστασης μεταξύ των αντικείμενων, και όπως αναφέρθηκε το αρχικό κίνητρο για την εισαγωγή της κοσμολογικής σταθεράς Λ, ήταν να γίνει δυνατό ένα στατικό σύμπαν που θα ήταν ισοτροπικό και ομοιογενές.
Μπορεί βέβαια ο Einstein να μην πρόβλεψε καμιά τιμή για τη σταθερά αυτή, αλλά η ιδέα μιας κοσμολογικής σταθεράς βρίσκεται το τελευταίο καιρό υπό συζήτηση. Φυσικοί προτείνουν σαν φυσική ερμηνεία της κοσμολογικής σταθεράς Λ ότι είναι απόρροια κβαντικών διαδικασιών στο αρχικό σύμπαν, όπως επίσης λένε ότι δείχνει πως οι διακυμάνσεις του κενού έχουν επιπτώσεις στο χωρόχρονο.
Είναι γεγονός ότι μέχρι τη δεκαετία του 1980 όλες οι αστρονομικές παρατηρήσεις ενίσχυαν τα κοσμολογικά μοντέλα στα οποία η κοσμολογική σταθερά Λ ήταν μηδέν. Ωστόσο, το 1980, η κοσμολογική σταθερά Λ ήλθε και πάλι στο προσκήνιο, στα πλαίσια του πληθωρισμικού μοντέλου
Σύμφωνα με το μοντέλο του πληθωρισμού σε χρόνο 10-35 sec μετά τη Μεγάλη Έκρηξη το σύμπαν άρχισε να διαστέλλεται με εκθετικό ρυθμό, δηλαδή με ταχύτητα πολύ μεγαλύτερη από αυτήν του φωτός. Η περίοδος της εκθετικής διαστολής διήρκεσε περίπου 10-32 sec ενώ η ενέργεια που απαιτήθηκε για την υλοποίηση της, προήλθε από τον διαχωρισμό της ισχυρής πυρηνικής δύναμης από την ασθενή πυρηνική και την ηλεκτρομαγνητική δύναμη που μέχρι τότε ήταν ενοποιημένες. Ο διαχωρισμός αυτός, που είναι ένα είδος αλλαγής φάσης, γέμισε το πρώιμο σύμπαν με ένα είδος ενέργειας που ονομάζεται ενέργεια του κενού και εκφράζεται από την κοσμολογική σταθερά Λ.
Όταν στα τέλη της δεκαετίας του ’90 ανακάλυψαν οι αστρονόμοι την επιταχυνόμενη διαστολή του σύμπαντος έκανε προφανή την ανάγκη ύπαρξης κάποιου είδους απωστικής βαρύτητας στο σύμπαν, που προκαλεί την επιτάχυνση και τη κοσμική διαστολή. Σύμφωνα με τις παρατηρήσεις, τα 2/3 περίπου της συνολικής ενέργειας του σύμπαντος, συμπεριλαμβανομένης της ύλης και της ακτινοβολίας, έχουν την ιδιότητα της βαρυτικής άπωσης. Η νέα αυτή μορφή ενέργειας ονομάστηκε σκοτεινή ενέργεια αφού δεν είναι ορατή ούτε μπορεί να συντεθεί από τη συνηθισμένη ατομική και υποατομική ύλη (κουάρκ, ηλεκτρόνια κλπ.).
Πολλοί επιστήμονες, ανάμεσα τους και ο Weinberg, πιστεύουν ότι η σκοτεινή ενέργεια είναι η ενέργεια του κενού, που εκφράζεται από την κοσμολογική σταθερά Λ. Όμως στο σημείο αυτό πρέπει να αναφέρουμε το λεγόμενο πρόβλημα της κοσμολογικής σταθεράς (cosmological constant problem).
Σύμφωνα με την αρχή της αβεβαιότητας, όλα τα κβαντικά πεδία, ακόμα και όταν βρίσκονται στη βασική μη διεγερμένη κατάσταση, έχουν μη μηδενική ενέργεια. Απλοί υπολογισμοί της κβαντικής θεωρίας πεδίου οδηγούν σε τιμές για την πυκνότητα της ενέργειας του κενού (δηλαδή για την κοσμολογική σταθερά Λ), που είναι 120 τάξεις μεγέθους (10120) μεγαλύτερη από την πυκνότητα της συνηθισμένης ύλης (όπως παρατηρείται στο σύμπαν). Όμως πρώτον, μια τόσο μεγάλη πυκνότητα ενέργειας του κενού χώρου θα προκαλούσε μια εκθετικά επιταχυνόμενη κοσμική διαστολή που θα διέλυε όλους τους ηλεκτροστατικούς και πυρηνικούς δεσμούς, οι οποίοι συγκρατούν τους πυρήνες, τα άτομα και τα μόρια.
Και δεύτερον μετρήσεις στο χώρο της κοσμολογίας δίνουν ένα αρνητικό αποτέλεσμα, δείχνοντας έτσι έναν ανώτερο όριο της κοσμολογικής σταθεράς Λ.
![]()
Έτσι, η τελευταία τιμή υπονοεί ότι στην συνολική κλίμακα του σύμπαντος, τα φαινόμενα των διακυμάνσεων του κενού ακυρώνονται. Κι αυτή η αξιολόγηση έρχεται και σε μία εποχή, που οι θεωρητικοί υπολογισμοί υποδεικνύουν συνεισφορές της διακύμανσης του κενού από τα κουάρκ με μια τάξη 10-6 m-2.
Μια άλλη διάσταση του προβλήματος της κοσμολογικής σταθεράς Λ έχει σχέση με τον χρόνο. Φαίνεται ότι ζούμε σε μια ξεχωριστή, προνομιούχο, περίοδο της κοσμικής εξέλιξης όπου η ενεργειακή πυκνότητα του κενού είναι, σε τάξη μεγέθους, ίση με την πυκνότητα της ύλης και της ακτινοβολίας στο σύμπαν. Η ενεργειακή πυκνότητα του κενού, αντίθετα από την πυκνότητα της ύλης και της ακτινοβολίας που ελαττώνονται με την πάροδο του χρόνου καθώς διαστέλλεται το σύμπαν και αυξάνεται ο όγκος του, παραμένει σταθερή. Αυτό σημαίνει ότι στο παρελθόν, όταν ο όγκος του σύμπαντος ήταν μικρότερος, η συνολική ενέργεια του κενού (που ισούται με την πυκνότητα επί τον όγκο) ήταν μικρότερη απ’ ό,τι σήμερα, δηλαδή ήταν λιγότερη από τη συνολική ποσότητα της ύλης και της ακτινοβολίας του σύμπαντος. Αντίστοιχα, με την πάροδο του χρόνου και καθώς θα αυξάνεται ο όγκος του σύμπαντος, θα αυξάνεται και η ενέργεια του κενού και κάποια στιγμή θα γίνει τάξεις μεγέθους μεγαλύτερη από την ύλη και την ακτινοβολία του σύμπαντος.
Τίθεται λοιπόν το ερώτημα: γιατί άραγε να υπάρχει αυτή η κοσμική σύμπτωση σήμερα; Γιατί δηλαδή στην παρούσα και όχι σε κάποια άλλη φάση της κοσμικής εξέλιξης, η ενεργειακή πυκνότητα του κενού συμβαίνει να είναι, σε τάξη μεγέθους, ίση (σε απόλυτες τιμές περίπου διπλάσια) με την πυκνότητα της ύλης και της ακτινοβολίας του σύμπαντος; Ζούμε άραγε σε μια ξεχωριστή περίοδο της κοσμικής εξέλιξης; Ποιός ξέρει;
Η πάρα πολύ μικρή τιμή της Λ – παρά την τεράστια τιμή που προβλέπεί η κβαντική θεωρία πεδίου – μπορεί να εξηγηθεί και από τη μείωση της ταχύτητας του φωτός. Σύμφωνα με μερικούς επιστήμονες η ταχύτητα του φωτός δεν είναι σταθερή στον χρόνο κι αυτό έχει πολλαπλές συνέπειες. Για παράδειγμα το μέτρο της βαρυτικής άπωσης – που εκφράζεται από τη σταθερά Λ – καθορίζεται εν μέρει από την τιμή της ταχύτητας του φωτός, γιατί το μέτρο της είναι ανάλογο του τετραγώνου της ταχύτητας του φωτός. Επομένως, μια αρκετά απότομη ελάττωση στην τιμή της ταχύτητας του φωτός στο πρώιμο σύμπαν, καθιστά αμελητέα την τιμή της κοσμολογικής σταθεράς Λ με την πάροδο του χρόνου.
Υπάρχουν όμως και διάφορες άλλες παρατηρήσεις που φανερώνουν την ανάγκη για μια κοσμολογική σταθερά.
Παραδείγματος χάριν, εάν η κοσμολογική σταθερά περιλαμβάνει σήμερα το μεγαλύτερο μέρος της ενεργειακής πυκνότητας του σύμπαντος, τότε η ηλικία του σύμπαντος που παρατηρούμε υπολογίζεται πολύ μεγαλύτερη από ό,τι θα ήταν, χωρίς τον όρο Λ στις εξισώσεις. Η ύπαρξη του κοσμολογικού όρου μας βοηθάει δηλαδή να αποφύγουμε το λάθος να υπολογίζουμε την ηλικία του σύμπαντος μικρότερη από την ηλικία μερικών από τα παλαιότερα αστέρια που έχουμε παρατηρήσει!
Για την πεμπτουσία και την εξέλιξη της κοσμολογικής σταθεράς
Οι παρατηρήσεις μας δείχνουν ότι το σύμπαν επεκτείνεται, περίπου, με διπλάσια ταχύτητα από αυτή που απαιτείται για να υπερνικήσει τη βαρυτική έλξη όλης της ύλης που περιέχει το σύμπαν. Η επίπτωση αυτού του γεγονότος είναι ότι κατά το παρελθόν η μεγαλύτερη πυκνότητα της μάζας επιβράδυνε με τη βοήθεια της βαρύτητας την διαστολή, ενώ στο μέλλον ο ρυθμός διαστολής θα είναι περίπου σταθερός ή ίσως και να αυξάνεται κάτω από την επίδραση ενός νέου τύπου ύλης που μερικοί φυσικοί αποκαλούν “πεμπτουσία”.
Η πεμπτουσία άρχισε ως η κοσμολογική σταθερά Λ του Αίνστάιν. Έχει αρνητική βαρυτική μάζα και η ‘βαρύτητα’ της είναι απωστική. Την είχαν προτείνει οι κοσμολόγοι Robert Caldwell, Paul Steinhardt και Rahul Dave σαν μια λύση για το πρόβλημα της τιμής που έχει η κοσμολογική σταθερά Λ. Σύμφωνα με το μοντέλο των Caldwell, Steinhardt και Dave, η σκοτεινή ενέργεια δεν είναι η ενέργεια του καμπυλωμένου χωροχρόνου αλλά ένα είδος αραιού «ρευστού» που γεμίζει το σύμπαν και ονομάζεται πεμπτουσία (quintessence). Στο μοντέλο αυτό, η τιμή της κοσμολογικής σταθεράς Λ είναι ακριβώς μηδέν όπως προκύπτει από την εφαρμογή μιας αρχής συμμετρίας που ονομάζεται υπερσυμμετρία και έτσι δεν υπάρχει πρόβλημα κοσμολογικής σταθεράς.
Η ενεργειακή πυκνότητα της πεμπτουσίας δεν είναι σταθερή αλλά μεταβάλλεται με τον χρόνο, παρακολουθεί και προσαρμόζεται στις αλλαγές της πυκνότητας της ύλης και της ακτινοβολίας του σύμπαντος. Η πεμπτουσία είναι μια δυναμική, χρονικά εξελισσόμενη και χωρικά ανομοιογενής μορφή ενέργειας που προκαλεί την επιτάχυνση της διαστολής του σύμπαντος. Υπάρχουν πολλές εκδοχές σχετικά με την πεμπτουσία, η κάθε μία με διαφορετικές ιδιότητες. Αντίθετα με την κοσμολογική σταθερά, η πεμπτουσία δεν είναι απαραίτητο να έχει κάποια συγκεκριμένη, προκαθορισμένη τιμή.
Τελευταία όμως το κυρίαρχο ρεύμα των φυσικών έχει υιοθετήσει την κοσμολογική σταθερά Λ, ως ένα καλό μοντέλο για τη βαρυτική επίδραση του ενεργού κενού της κβαντικής φυσικής και δεν δίνει σημασία στην πεμπτουσία.
Οι θεωρητικοί κοσμολόγοι πιστεύουν επίσης ότι καθώς το σύμπαν επεκτείνεται και ψύχεται, η σταθερά Λ του Αϊνστάιν τείνει να μειωθεί. Καθώς το σύμπαν ψύχεται, οι συμμετρίες μεταξύ των δυνάμεων σπάζουν, τα σωματίδια αποκτούν μάζες, και αυτές οι διαδικασίες τείνουν να απελευθερώσουν μια ανάλογη της λανθάνουσας θερμότητας. Η ενεργειακή πυκνότητα του κενού μειώνεται αναλόγως, και μαζί με αυτήν η τιμή του Λ.
Ίσως ένα τεράστιο Λ οδήγησε το σύμπαν σε μια γρήγορη επέκταση που ‘λείανε’ το αρχέγονο χάος για να κάνει σχεδόν το ομοιόμορφο σύμπαν που βλέπουμε σήμερα, ενώ όσο περνά ο χρόνος μειώνεται η τιμή της Λ. Αυτή η κοσμολογική άποψη ανήκει στη θεωρία του πληθωριστικού σύμπαντος στις απαρχές του.
Σημείωση: οι κβαντικοί φυσικοί όταν μιλάνε για ενεργό κενό αναφέρονται στην άποψη ότι η κατάσταση του κενού έχει μια ενέργεια μηδενικού σημείου (μια ελάχιστη ενέργεια), που προκαλεί τις διακυμάνσεις του κενού. Έτσι η κενή κατάσταση δεν σημαίνει μια κατάσταση του τίποτα, αλλά αντιθέτως είναι μια ενεργή κατάσταση.
Για μια πιο βαθιά μελέτη
Sean Carroll’s Living Review: The Cosmological Constant.
T. Padmanabhan, Dark Energy and Gravity
Ned Wright, Vacuum Energy Density, or How Can Nothing Weigh Something?
Subir Sarkar: Is the evidence for dark energy secure?
Wikipedia on The Cosmological Constant



