Καθώς αναπτυσσόταν το Καθιερωμένο Μοντέλο για τα σωματίδια, οι φυσικοί παρατήρησαν ότι ορισμένες αλληλεπιδράσεις και διασπάσεις ήταν επιτρεπτές, ενώ άλλες φαίνονταν πως ήταν απαγορευμένες. Έτσι η μελέτη των αλληλεπιδράσεων οδήγησε τους φυσικούς σε νέους κβαντικούς αριθμούς (εκτός των γνωστών spin, στροφορμής, κύριου μαγνητικού αριθμού, δευτερεύοντος κβαντικού αριθμού κλπ), και ένα νέο σύνολο νόμων διατήρησης, που κυβερνούν τις αλληλεπιδράσεις όλων των σωματιδίων. Οι νέοι κβαντικοί αριθμοί έχουν δε ανατεθεί σε νέα σωματίδια με παράξενες ιδιότητες.
Εισαγωγή
Υπάρχει μια αρχή στην Φυσική, που λέει ότι "αν μια διαδικασία δεν απαγορεύεται, τότε μπορεί να συμβεί". Από αυτήν την άποψη, οποιαδήποτε διαδικασία διάσπασης που αναμένεται αλλά δεν παρατηρείται, πρέπει να αποτρέπεται από κάποιο νόμο διατήρησης. Αυτή η προσέγγιση είναι κατάλληλη για να καθοριστούν οι κανόνες για την διάσπαση των σωματιδίων.
Οι σπουδαιότεροι νόμοι διατήρησης είναι δύο. Η διατήρηση του ολικού ηλεκτρικού φορτίου και του βαρυονικού αριθμού. Και οι δύο ισχύουν για όλες τις αλληλεπιδράσεις.
Αλλά προχωρώντας στη μελέτη των αλληλεπιδράσεων μεταξύ των σωματιδίων, οι φυσικοί εκχώρησαν νέους κβαντικούς αριθμούς για να μπορούν να δικαιολογήσουν την παρατήρηση τους. Συγχρόνως έχουμε και τους αντίστοιχους νόμους της διατήρησης τους. Οι σπουδαιότεροι από αυτούς είναι ο λεπτονικός αριθμός , το ισοτοπικό σπιν, η παραδοξότητα, η γοητεία, το χρώμα, το υπερφορτίο.
Υπάρχουν όμως κι άλλοι σπουδαίοι νόμοι διατήρησης, όπως για την ομοτιμία, την χρονική αντιστροφή και το φορτίο που έχουν αναπτυχθεί λόγω λεπτομερούς παρατήρησης των σωματιδιακών αλληλεπιδράσεων. Όμως ο συνδυασμός του κατοπτρισμού ως προς το φορτίο C (Charge Conjugation), της ομοτιμίας (P) και της χρονικής αντιστροφής (T) θεωρείται μια θεμελιώδης λειτουργία συμμετρίας – όλων των φυσικών σωματιδίων και όλες οι αλληλεπιδράσεις εμφανίζονται να είναι αμετάβλητες κάτω από αυτόν τον συνδυασμό. Αυτή η συμμετρία που καλείται CPT αμεταβλητότητα , έχει μεγάλο βάρος στην κατανόησή που έχουμε για τις διαδικασίες διάσπασης στη Φύση.
Βαρυονικός αριθμός Β
Οι φυσικοί έδωσαν βαρυονικό αριθμό Β μηδέν στο φωτόνιο, στα λεπτόνια (ηλεκτρόνια, μιόνια, ταυ, νετρίνα) και στα μεσόνια. Επίσης για τα βαρυόνια (νετρόνια, πρωτόνια) ανατίθεται ο βαρυονικός αριθμός Β=1, ενώ στα αντιβαρυόνια δίνεται ο Β=-1. Τα συστατικά όμως των βαρυονίων είναι τα κουάρκ, στα οποία ανατίθεται ο βαρυονικός αριθμός Β=1/3, ενώ στα αντικουάρκ -1/3. Επειδή όμως ισχύει η προσθετική ιδιότητα στον βαρυονικό αριθμό, το άθροισμά τους δίνει 1 για τα βαρυόνια, όπως είδαμε πριν. Αυτό όμως υπονοεί ότι τα μεσόνια , με ένα κουάρκ και ένα αντικουάρκ, έχουν έναν βαρυονικό αριθμό B=0.
Καμία γνωστή διαδικασία ή αλληλεπίδραση διάσπασης στη φύση δεν αλλάζει τον καθαρό βαρυονικό αριθμό, γιατί το άθροισμα των βαρυονικών αριθμών πριν την πυρηνική αντίδραση ή διάσπαση πρέπει να είναι ίσο με το άθροισμα των βαρυονικών αριθμών μετά από αυτήν.
Το νετρόνιο, και όλα τα βαρύτερα βαρυόνια, διασπάται κατευθείαν σε πρωτόνιο ή σχηματίζουν τελικά πρωτόνια, το σωματίδιο που είναι το λιγότερο ογκώδες βαρυόνιο. Δίνοντας όμως Β=1 στο ελαφρύτερο βαρυόνιο, αυτό υπονοεί ότι το πρωτόνιο δεν μπορεί να διασπαστεί σε άλλα σωματίδια, γιατί αλλιώς παραβιάζεται η αρχή της διατήρησης του βαρυονικού αριθμού. Μια πρόβλεψη της Μεγάλης Ενοποίησης των δυνάμεων είναι ότι το πρωτόνιο θα είχε τη δυνατότητα της διάσπασης, έτσι ώστε αυτή η δυνατότητα ερευνάται πειραματικά .
Δηλαδή η διατήρηση του βαρυονικού αριθμού (Β) απαγορεύει μια διάσπαση του παρακάτω τύπου, γιατί ο Β δεν παραμένει σταθερός.
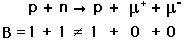
Αλλά, από την άλλη μεριά, αν υπάρχει αρκετή ενέργεια, επιτρέπεται η παραγωγή ενός ζεύγους σωματιδίων στην παρακάτω αντίδραση (γιατί ο αριθμός Β διατηρείται).
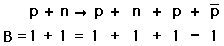
Το γεγονός ότι παρατηρείται η διάσπαση στο μεσόνιο π,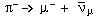 
, υπονοεί ότι δεν υπάρχει καμία αντίστοιχη αρχή της διατήρησης του αριθμού των μεσονίων. Το πιόνιο είναι ένα μεσόνιο που αποτελείται από ένα κουάρκ και ένα αντικουάρκ, και στη δεξιά πλευρά της εξίσωσης υπάρχουν μόνο λεπτόνια. (Αυτή η διάσπαση μας δείχνει ότι μπορείται να αναθέσετε έναν βαρυονικό αριθμό 0 στο μεσόνιο.)
Λεπτονικός αριθμός L
Επειδή υπάρχουν τρείς οικογένειες λεπτονίων (ηλεκτρόνιο με το νετρίνο του, μιόνιο με το νετρίνο του και ταυ με το νετρίνο του), αυτός ο κανόνας είναι λίγο πιό περίπλοκος από τη διατήρηση του βαρυονικού αριθμού, επειδή υπάρχει μια ξεχωριστή απαίτηση για διατήρηση του λεπτονικού αριθμού σε κάθε ένα από τα τρία σύνολα των λεπτονίων.
Έτσι πρέπει το άθροισμα των λεπτονικών αριθμών των μελών της ίδιας οικογένειας, πριν την αντίδραση να ισούται με το άθροισμα των λεπτονικών αριθμών, μετά την αντίδραση.
Το πρώτο σημαντικό παράδειγμα βρέθηκε στη περίφημη διάσπαση του νετρονίου. Όταν παρατηρήθηκε η διάσπαση του νετρονίου σε ένα πρωτόνιο και ένα ηλεκτρόνιο, δεν ταίριαζε στο πρότυπο της διάσπασης προς δύο νέα σωματίδια. Επειδή το εκπεμπόμενο ηλεκτρόνιο δεν έχει μια καθορισμένη ενέργεια, όπως απαιτείται από τη διατήρηση της ενέργειας και της ορμής σε μια διάσπαση προς δύο σωμάτια, αυτό μας έκανε να σκεφθούμε ότι εκπέμπεται κι ένα τρίτο σωματίδιο, το οποίο καθορίστηκε σαν το αντινετρίνο των ηλεκτρονίων.
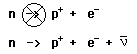
Αν αναθέσουμε ένα νέο κβαντικό αριθμό, το λεπτονικό αριθμό L=1 στο ηλεκτρόνιο και L=-1 στο αντινετρίνο του ηλεκτρονίου, τότε διατηρείται ο λεπτονικός αριθμός ίσος με μηδέν και στις δύο πλευρές της δεύτερης αντίδρασης πιό πάνω, ενώ η πρώτη αντίδραση δεν διατηρεί το λεπτονικό αριθμό. Φυσικά ο βαρυονικός αριθμός Β, διατηρείται στην διάσπαση του νετρονίου.
Η παρατήρηση των ακόλουθων δύο διαδικασιών διάσπασεων οδηγεί στο συμπέρασμα ότι υπάρχει ένας ξεχωριστός λεπτονικός αριθμός για τα μιόνια που πρέπει επίσης να διατηρείται.
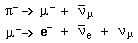
Η πρώτη αντίδραση ανωτέρω (διάσπαση πιονίου) είναι γνωστή ότι είναι μια διάσπαση προς δύο σωμάτια, από το γεγονός ότι παρατηρείται από την διάσπαση, μια καλά καθορισμένη ενέργεια του μιονίου. Εντούτοις, η διάσπαση του μιονίου σε ένα ηλεκτρόνιο παράγει μια γκάμα (ένα σύνολο) ενεργειών των ηλεκτρονίων, που δείχνουν ότι είναι τουλάχιστον διάσπαση προς τρία σωμάτια. Για να διατηρείται λοιπόν και ο λεπτονικός αριθμός των ηλεκτρονίων και ο λεπτονικός αριθμός των μιονίων, τότε τα άλλα σωματίδια πρέπει να είναι ένα αντι-νετρίνο του ηλεκτρονίου και ένα νετρίνο του μιονίου.
Ισοσπίν Ι
Το ισοσπίν I, είναι ένας όρος που εισάγεται για να περιγράψει τις ομάδες των σωματιδίων που παρουσιάζονται σε δύο ή και τρεις μορφές. Πχ το νουκλεόνια παρουσιάζεται σε δύο μορφές που έχουν σχεδόν την ίδια μάζα, όπως το πρωτόνιο και το νετρόνιο (938,27 MeV το πρωτόνιο και 939,56 MeV το νετρόνιο). Μπορούμε να αναθέσουμε λοιπόν ένα νέο κβαντικό αριθμό στο νουκλεόνιο το ισοσπίν I, με τιμή 1/2. Επειδή αποτελείται από δύο σωματίδια, στο πρωτόνιο αντιστοιχεί η τιμή +1/2 και η τιμή -1/2 στο νετρόνιο. Τον όρο αυτό τον δανείστηκαν από το σπιν του ηλεκτρονίου, γιατί όπως το σπιν του ηλεκτρονίου έχει δύο καταστάσεις, η μία με πάνω σπιν α και η άλλη με κάτω σπιν κ, έτσι και το ισοσπίν έχει δύο καταστάσεις.
Ομοίως, το πιόνιο παρουσιάζεται τρεις μορφές, που συνθέτουν ένα τρίδυμο, ένα θετικό, ένα ουδέτερο κι ένα αρνητικό πιόνιο. Στο πιόνιο αναθέτουμε το Ισοσπίν Ι=1, άρα στο καθένα πιόνιο αναθέτουμε Ισοσπίν + 1 για το θετικό, 0 για το ουδέτρο και -1 για το αρνητικό πιόνιο.
Το Ισοσπίν συνδέεται με το γεγονός ότι η ισχυρή αλληλεπίδραση είναι ανεξάρτητη από το ηλεκτρικό φορτίο. Οποιαδήποτε δυάδα σωματιδίων, όπως το πρωτόνιο – νετρόνιο, με ισοσπίν, δοκιμάζουν την ίδια ισχυρή αλληλεπίδραση: Για παράδειγμα, τα ζεύγη πρωτόνιο-πρωτόνιο, πρωτόνιο-νετρόνιο, νετρόνιο-νετρόνιο δέχονται την ίδια ισχυρή ελκτική δύναμη.
Στο επίπεδο των κουάρκ, τα πάνω (up) και κάτω (down) κουάρκ διαμορφώνουν επίσης μια δυάδα σωματιδίων με ισοσπίν (I=1/2) και η προβολή (τιμή) + 1/2 ανατίθεται στο up και η προβολή 1/2 στο down κουάρκ. Το παράξενο (strange) κουάρκ είναι σε μια κλάση μόνο του, κι έχει Ισοσπίν I=0. Το Ισοσπίν συσχετίζεται με άλλους κβαντικούς αριθμούς για τα σωματίδια ως εξής:
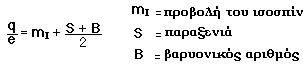
Όπως κάθε κβαντικός αριθμός έτσι και το Ισοσπίν συνδέεται με ένα νόμο διατήρησης, όπως φαίνεται στην παρακάτω διαδικασία:
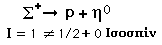
Η ανωτέρω διάσπαση δεν έχει παρατηρηθεί ποτέ, αν και διατηρείται σε αυτήν το φορτίο, η στροφορμή και ο βαρυονικός αριθμός. Είναι λοιπόν μια απαγορευμένη διάσπαση επειδή δεν διατηρείται ο κβαντικός αριθμός του Ισοσπίν Ι.
Παραξενιά S
Πριν τη λειτουργία των μεγάλων επιταχυντών πολλά ανακαλυφθέντα σωματίδια, τη δεκαετία του 1950, είχαν παραχθεί σε αντιδράσεις των πιονίων, της κοσμικής ακτινοβολίας, με τα πρωτόνια και νετρόνια της ατμόσφαιρας. Μια ομάδα εξ’ αυτών, το Κ, το Λ και το Σ, είχαν μια παράξενη ιδιότητα η οποία παρουσιάζεται κατά τη παραγωγή τους ή τη διάσπασή τους. Για τον λόγο αυτό τα σωματίδια αυτά ονομάστηκαν παράξενα ή παράδοξα σωματίδια (strange particles).
Μια παράξενη ιδιότητά τους είναι ότι παράγονται σε ζεύγη. Έτσι όταν ένα αρνητικό πιόνιο συγκρουστεί με ένα πρωτόνιο, μπορεί να συντελεστεί η παρακάτω αντίδραση, η οποία έχει παρατηρηθεί επανειλημμένα στη φύση: π– + p —> Kο + Λο
Οι αντιδράσεις παραγωγής, όπως π.χ. π– + p —> Kο + n, στις οποίες παράγεται μόνο ένα πιόνιο (το Kο ή το Λο ή το Σ) δεν συντελούνται ποτέ, παρόλο που δεν υπάρχει κανένας γνωστός νόμος διατήρησης να τις απαγορεύει.
Το άλλο περίεργο των παράξενων σωματιδίων είναι ότι, αν και παράγονται από τις ισχυρές αλληλεπιδράσεις , δεν διασπώνται αρκετά συχνά σε αδρόνια εξ’αιτίας τους. Ο χρόνος μάλιστα ζωής τους είναι αρκετά μεγάλος και η διάσπασή τους θυμίζει ασθενείς αλληλεπιδράσεις. Ενώ τα αδρόνια που διασπώνται λόγω των ισχυρών αλληλεπιδράσεων έχουν χρόνο ζωής 10-22 sec, εδώ έχουμε χρόνους 10-8 έως 10-10sec, που θυμίζουν ασθενείς αλληλεπιδράσεις.
Για την ερμηνεία του φαινομένου διατυπώθηκε ο νόμος της διατήρησης της παραξενιάς η παραδοξότητας και εισάγεται έτσι ένας νέος κβαντικός αριθμός, ο κβαντικός αριθμός της παραξενιάς S.
Στην ανωτέρω αντίδραση που παράγονται δύο παράξενα σωματίδια, το Kο και το Λο, δίνεται ο S=+1 στο ένα σωματίδιο και S=-1 στο άλλο. Τα αδρόνια που δεν είναι παράξενα πχ τα πιόνια και όλα τα λεπτόνια έχουν S=0.
Επίσης βλέπουμε ότι το άθροισμα της παραξενιάς πριν και μετά την αντίδραση διατηρείται σταθερό.
Υπερφορτίο Υ
Μια άλλη ακέραια ποσότητα που διατηρείται στις ισχυρές και ηλεκτρομαγνητικές αλληλεπιδράσεις είναι το υπερφορτίο Υ. Οι ασθενείς φαίνονται να μην διατηρούν το υπερφορτίο. Μπορούμε να δώσουμε έναν κβαντικό ακέραιο αριθμό σε κάθε σωματίδιο που αλληλεπιδρά ισχυρά κατά τέτοιο τρόπο, ώστε το ολικό υπερφορτίο να διατηρείται.
Δίνεται από τη σχέση Υ=Β+S και η επιλογή αυτή δεν έχει καμμιά φυσική σημασία, αλλά βοηθάει την ταξινόμηση των στοιχειωδών σωματιδίων.
Η αντίδραση π– + p —> Kο + Λο επιτρέπεται, και συμβαίνει κι’ εύκολα, γιατί όταν αναθέσουμε τους παρακάτω αριθμούς υπερφορτίου Υ: στο π–=0, στο p=+1, στο Kο=+1 και στο Λο=0, τότε το υπερφορτίο Υ διατηρείται.
Αλλά η αντίδραση π– + p —> πο + Λο δεν επιτρέπεται, δεν την έχουμε ποτέ παρατηρήσει, γιατί στο πο αν αναθέσουμε Υ=0, τότε δεν διατηρείται ο κβαντικός αριθμός υπερφορτίου Υ.
Η παρακάτω αντίδραση επειδή συμβαίνει αργά, περίπου 10-10sec, είναι υπεύθυνες οι ασθενείς αλληλεπιδράσεις, στις οποίες δεν ισχύει η διατήρηση του υπερφορτίου κι έτσι πραγματοποιείται παρόλο που δεν διατηρείται ο κβαντικός αριθμός Υπερφορτίου Υ: Λο —> π– + p
Ομοτιμία P
Ένας από τους πιό φημισμένους νόμους διατήρησης που ισχύει για τις αλληλεπιδράσεις μεταξύ των σωματιδίων, συνδέεται με την ομοτιμία P (parity).
Τα κουάρκ έχουν μια εγγενή ισοτιμία που καθορίζεται να είναι + 1 και για τα αντικουάρκ η ισοτιμία τους = -1,
Για ένα μεσόνιο όμως, με ένα κουάρκ κι ένα αντικουάρκ με αντιπαράλληλα spin (s=0), τότε η ομοτιμία δίνεται από τη σχέση :
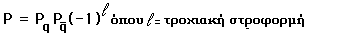
Η ομοτιμία των μεσονίων δίνεται από τη σχέση
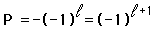
Όλα τα νετρίνα βρίσκονται πως είναι "αριστερόχειρα", με μια εγγενή ομοτιμία P= -1 ενώ τα αντινετρίνα είναι δεξιόχειρα, με ομοτιμία P = + 1.
Η παραβίαση της ομοτιμίας και το καόνιο
Τα ουδέτερα καόνια είναι σημαντικά ιστορικά σωματίδια για τη συνεισφορά που έχουν για τη κατανόηση των διαδικασιών στα κουάρκ. Όταν ανακαλύφθηκαν αρχικά προς το τέλος της δεκαετίας του ’40 ονομάστηκαν μεσόνια τ και θ, και η αποσύνθεσή τους ήταν ένα μεγάλο μυστήριο, οι φυσικοί δε ονόμασαν αυτό το γρίφο τ-θ. Τα σωματίδια είχαν ακριβώς την ίδια μάζα, και το μόνο πράγμα που τα διαφοροποιούσε προφανώς ήταν οι διαδικασίες αποσύνθεσής τους και το γεγονός ότι τα δύο διαφορετικά σύνολα προϊόντων διάσπασης είχαν διαφορετική ομοτιμία.
Οι διασπάσεις των σωματιδίων από τις ισχυρές ή τις ηλεκτρομαγνητικές αλληλεπιδράσεις είχαν παρατηρηθεί πως διατηρούσαν την ομοτιμία στις διασπάσεις τους Οι θεωρητικοί φυσικοί Τ. D. Lee και C. Ν. Yang πρότειναν το 1956 ότι η ομοτιμία δεν χρειάζεται να διατηρείται στις ασθενείς αλληλεπιδράσεις διασπάσεων. Το 1957 η Chien-Shiung Wu εμφάνισε αυτήν την παραβίαση, της διατήρησης της ομοτιμίας, στη βήτα διάσπαση του κοβαλτίου. Ακόμη και με την παραβίαση της ομοτιμίας, θεωρήθηκε ότι ο συνδυασμός του κατοπτρισμού ως προς το φορτίο C και της ομοτιμίας θα άφηνε το σύστημα αμετάβλητο. (σταθερότητα CP). Ένα πείραμα που έγινε από τους Cronin και Fitch το 1964, πήραν το 1980 Nobel Φυσικής, έδειξε ότι υπήρξε μια μικρή παραβίαση CP στην αποσύνθεση του καονίου. Έτσι το καόνιο έχει διαδραματίσει έναν κεντρικό ρόλο στις συζητήσεις αυτών των συμμετριών από τότε.
Το 1946 οι Rochester και Butler ανακάλυψαν ένα είδος του ουδέτερου καονίου μικρής διάρκειας, κι έτσι παρατήρησαν ένα χαρακτηριστικό σχήμα "V" στο θάλαμο φυσσαλίδων. Η διάσπαση που αυτοί είδαν ήταν η εξής:
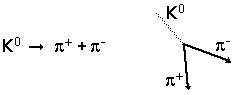
Το ουδέτερο Καόνιο δεν άφηνε ίχνος στο θάλαμο φυσαλίδων, έτσι λοιπόν το ίχνος "V" των πιονίων απέδειξε την παρουσία του, με τη διάσπασή του καονίου.
Η περιγραφή των ουδέτερων καονίων είναι σύνθετη και παράξενη. Υπάρχουν δύο εκδόσεις αυτού του σωματιδίου με την ίδια μάζα, αλλά διαφορετική χρονική διάρκεια αποσύνθεσης! Το ένα καλείται Κο short με χρόνο ζωής 9×10-11 sec και το άλλο καλείται Κο long με χρόνο ζωής 9×10-8 sec .
Τα ουδέτερα καόνια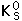 
και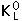 
αντιπροσωπεύουν τα συμμετρικά και αντισυμμετρικά μίγματα των συνδυασμών των κουάρκ down – antistrange και antidown – strange.
Ενώ τα φορτισμένα καόνια είναι μεσόνια που έχουν μια σύνθεση κουάρκ up – antistrange για το θετικό καόνιο και antiup – strange για το αρνητικό καόνιο. Αποσυντίθονται σε περίπου 10-8 δευτερόλεπτα με τις εξής διαδικασίες:
και
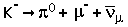
Αναφορές: Σύγχρονη Φυσική Serway, Μαθήματα Φυσικής του Berkeley, Εκπαιδευτική Εγκυκλοπαίδεια, CERN, Uni of Stanford, Ιστοσελίδα της Φυσικής στο ΕΜΠ, Πανεπιστημιακή Φυσική του Blatt
Διαβάστε οπωσδήποτε και Η συμμετρία στη Φυσική – Η έννοια της συμμετρίας στους νόμους της Φυσικής
Leave a Comment