Η Μουσική του Πλέγματος: ένα ποίημα σε δυο εξισώσεις

Οι μάζες των σωματιδίων απηχούν τις συχνότητες με τις οποίες δονείται ο χώρος όταν παίζεται η μουσική του. Αυτή η Μουσική του Πλέγματος υπερβαίνει την κεντρική ιδέα των παλιών μυστικών, τη «Μουσική των Σφαιρών», τόσο σε φαντασιακό όσο και σε ρεαλιστικό επίπεδο.

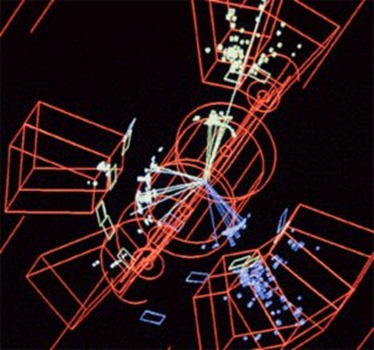Φωτογραφία που έχει ληφθεί στον LEP, τον επιταχυντή ο οποίος λειτούργησε στο CERN κατά τη δεκαετία του 1990. Οι πίδακες σωματιδίων που αναδύονται από αυτές τις συγκρούσεις ακολουθούν τα θεωρητικώς προβλεπόμενα μοτίβα ροής για ένα κουάρκ, ένα αντικουάρκ και ένα γλοιόνιο. Οι πίδακες δίνουν λειτουργικό νόημα σε αυτές τις οντότητες, οι οποίες δεν μπορούν να παρατηρηθούν με τη συνήθη έννοια, υπό μορφή σωματιδίων.

(…) Ας συνδυάσουμε την εξίσωση Einstein με μια άλλη θεμελιώδη εξίσωση, τον τύπο Planck – Einstein – Schrödinger .

Ο τύπος Planck – Einstein – Schrödinger συσχετίζει την ενέργεια μιας κβαντομηχανικής κατάστασης με τη συχνότητα με την οποία δονείται η κυματοσυνάρτησή της. Με συμβολίζουμε τη σταθερά του Planck. Ο Planck εισήγαγε την εν λόγω εξίσωση με την επαναστατική υπόθεσή του (1899), η οποία αποτέλεσε το έναυσμα της κβαντικής θεωρίας – ότι δηλαδή, τα άτομα εκπέμπουν ή απορροφούν φως συχνότητας μόνο υπό τη μορφή πακέτων ενέργειας .

Στη συνέχεια, ο Αϊνστάιν έκανε ένα μεγάλο βήμα μπροστά με την υπόθεσή του για τα φωτόνια (1905) – ότι, δηλαδή, το φως συχνότητας εμφανίζεται πάντοτε υπό μορφή πακέτων ενέργειας .

Τέλος, ο Schrödinger θεμελίωσε με τον τύπο αυτό τη βασική του εξίσωση για τις κυματοσυναρτήσεις – την εξίσωση Schrödinger (1926). Έτσι γεννήθηκε η σύγχρονη, καθολική ερμηνεία: η κυματοσυνάρτηση μιας κατάστασης με ενέργεια δονείται με συχνότητα , η οποία δίνεται από τον τύπο .

Συνδυάζοντας τον Αϊνστάιν με τον Schrödinger , καταλήγουμε σε ένα θαυμαστό δείγμα ποίησης:

(1)

Οι αρχαίοι διέθεταν μια έννοια, τη «Μουσική των Σφαιρών», η οποία ενέπνευσε πολλούς επιστήμονες (με πιο διάσημο τον Johannes Kepler) και ακόμη περισσότερους μυστικιστές. Η ιδέα ήταν ότι, εφόσον η περιοδική κίνηση (δόνηση) των μουσικών οργάνων προκαλεί τους σταθερούς τόνους τους, τότε η περιοδική κίνηση των πλανητών, καθώς αυτοί διατρέχουν τις τροχιές τους, θα πρέπει να συνοδεύεται από ένα είδος μουσικής.
Αν και μοιάζει με γραφική περιγραφή ηχητικών τοπίων, αυτή η γαργαλιστική πρόβλεψη των πολυμέσων δεν εξελίχθηκε ποτέ σε γόνιμη ή μεγάλης ακρίβειας επιστημονική ιδέα. Δεν υπήρξε ποτέ κάτι περισσότερο από μια ασαφής μεταφορά, γι’ αυτό και παραμένει εντός εισαγωγικών: «Μουσική των Σφαιρών».

Η εξίσωση (1) αποτελεί μια πιο εξωτική, ωστόσο περισσότερο ρεαλιστική ενσάρκωση της ίδιας έμπνευσης: Αντί να τεντώνουμε μια χορδή, να φυσάμε μέσα από έναν αυλό, να χτυπάμε ένα τύμπανο ή ένα γκογκ, παίζουμε το όργανο που είναι κενός χώρος, χτυπώντας διαφορετικούς συνδυασμούς κουάρκ, γλοιονίων, ηλεκτρονίων, φωτονίων … (δηλαδή, τις δομικές μονάδες που αντιπροσωπεύουν αυτά τα Πράγματα), και το αφήνουμε να σταθεροποιηθεί, ώσπου να φτάσει σε ισορροπία με την αυθόρμητη δραστηριότητα του Πλέγματος*. Ούτε οι πλανήτες ούτε οποιαδήποτε άλλη υλική κατασκευή δεν θίγει την αγνή ιδανικότητα του οργάνου μας. Αυτό σταθεροποιείται σε μια από τις δυνατές δονητικές κινήσεις του (διαφορετικών συχνοτήτων ), ανάλογα με το πώς (και με τι) το χτυπάμε. Σύμφωνα με την εξίσωση (1), οι εν λόγω δονήσεις αναπαριστούν σωματίδια διαφορετικών μαζών . Οι μάζες των σωματιδίων απηχούν τη Μουσική του Πλέγματος (…)

Απόσπασμα από το βιβλίο του Frank Wilczek, «Η ελαφρότητα του είναι», εκδόσεις κάτοπτρο

(*) Ο Frank Wilczek χρησιμοποιεί τον όρο Πλέγμα για το πρωταρχικό υλικό του κόσμου, αποφεύγοντας τη λέξη χωρόχρονος που βαρύνεται με έντονες συνδηλώσεις περί κενότητας, η τον όρο κβαντικό πεδίο, τον οποίο θεωρεί τεχνικό όρο και απαγορευτικό για να χρησιμοποιηθεί στη φυσική φιλοσοφία.

Πηγή