Η γοητεία που ασκούν τα μαθηματικά στον ανθρώπινο εγκέφαλο επιβεβαιώνεται μέσω μίας νέας βρετανικής επιστημονικής έρευνας σύμφωνα με την οποί όσοι θεωρούν πραγματικά όμορφες τις εξισώσεις, τις βλέπουν σαν αυθεντικά έργα τέχνης. Η νέα μελέτη ενισχύει τη θεωρία ότι υπάρχει μια ενιαία νευροβιολογική βάση για την ομορφιά και την αισθητική αντίληψη του ωραίου.
Οι ερευνητές, με επικεφαλής τον καθηγητή Semir Zeki του Εργαστηρίου Νευροβιολογίας Wellcome του University College του Λονδίνου, που έκαναν τη σχετική δημοσίευση στο περιοδικό «Frontiers in Human Neuroscience», (Σύνορα στην Ανθρώπινη Νευροεπιστήμη), χρησιμοποίησαν την τεχνική της λειτουργικής μαγνητικής απεικόνισης (fMRI) για να μελετήσουν την εγκεφαλική δραστηριότητα 15 εθελοντών μαθηματικών, την ώρα που αυτοί καλούνταν να δουν 60 μαθηματικές εξισώσεις και να τις αξιολογήσουν ως όμορφες, άσχημες ή ουδέτερες.
Ταυτότητα Euler: Δείγμα μεγάλης μαθηματικής ομορφιάς
Η μελέτη έδειξε ότι η εμπειρία του «μαθηματικά ωραίου» καταγράφεται στην ίδια συναισθηματική περιοχή του εγκεφάλου (στον μέσο κογχομετωπιαίο φλοιό), όπου αποτυπώνεται και γίνεται η επεξεργασία του «ωραίου» στην μουσική ή τη ζωγραφική.
Ο θεωρητικός φυσικός Paul Dirac με την τεράστια επιρροή έχει δηλώσει: «Αυτό που κάνει τη θεωρία της σχετικότητας, τόσο αποδεκτή από τους φυσικούς παρά του ότι είναι ενάντια στην αρχή της απλότητας, είναι η μεγάλη μαθηματική ομορφιά της. Έχει μια ποιότητα που δεν μπορεί να προσδιοριστεί, περισσότερο από ό,τι η ομορφιά στη τέχνη, αλλά που οι άνθρωποι οι οποίοι μελετούν τα μαθηματικά δεν έχουν συνήθως καμία δυσκολία να την εκτιμήσουν. “
«Σε πολλούς από εμάς οι μαθηματικές εξισώσεις φαίνονται ξερές και ακατανόητες, όμως για έναν μαθηματικό μια εξίσωση μπορεί να ενσωματώνει την πεμπτουσία της ομορφιάς. Η ομορφιά μιας εξίσωσης μπορεί να προέρχεται από την απλότητά της, τη συμμετρία της, την κομψότητά της ή την έκφραση μιας αναλλοίωτης αλήθειας. Για τον Πλάτωνα, η αφηρημένη ποιότητα των μαθηματικών εξέφραζε το αποκορύφωμα της ομορφιάς», δήλωσε ο Semir Zeki.
Το πείραμα έδειξε ότι οι εξισώσεις που συστηματικά γεννούν την πιο έντονη αισθητική απόλαυση, είναι η ταυτότητα του Όιλερ, το Πυθαγόρειο θεώρημα και οι εξισώσεις Cauchy-Riemann (ένα ζευγάρι πραγματικών συναρτήσεων με δύο πραγματικές μεταβλητές u (x, y) και v (x, y):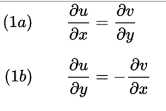 
ΑΠΕ
