Το Χάος στις Κοσμογονίες
Η αιώνια πάλη μεταξύ τάξης και αταξίας, αρμονίας και χάους, αντιπροσωπεύει, μάλλον μια βαθιά ριζωμένη αντίληψη του ανθρώπου για το σύμπαν. Γι’ αυτό και τη συναντάμε σε τόσους πολλούς μύθους για τη δημιουργία του κόσμου και σε τόσους πολλούς πολιτισμούς.
Το Χάος ήταν το πρώτο στοιχείο της κοσμογονίας των φιλοσόφων της αρχαίας Ελλάδας. Για πρώτη φορά το “Χάος” παρουσιάζεται στην Θεογονία του Ησιόδου (8ος αιώνας π.Χ.) σαν η πρωταρχική ύλη του Κόσμου που που οδηγείται μέσα από την εξελικτική πορεία μιας αέναης μεταβολής της ύλης και της κίνησης από το ομοιόμορφο στο πολύμορφο:
Το Χάος πρωτογίνηκε κι η Γη μετά η πλατυστήθα … Κι απ’ το Χάος πάλιν γεννήθηκε το Έρεβος και η τρίσμαυρη η Νύχτα…
Και μετά έρχεται η ισορροπία, η αρμονία και η ζωή. Αλλά η ανθρώπινη ζωή βιώνεται μέσα σε ένα χαοτικό κόσμο, την πολυπλοκότητα, τις αντιθέσεις και την αντίφαση που κυριαρχούν σε όλους τους τομείς της σκέψης και της ζωής. Από τις αντιθέσεις δε προκύπτει η τέλεια σύνθεση, όπου τυχαία και συγκεχυμένα στοιχεία της υπάρχουσας άπειρης ύλης, μορφοποιούνται σε συντεταγμένες καταστάσεις.
Ο Αναξιμένης (585 περίπου π.Χ.), ένας σοφός από τη Μίλητο και μαθητής του Αναξίμανδρου, δίνει την εξήγηση των διαφόρων μορφών της πρωταρχικής ύλης, του Χάους, με την πύκνωση και την αραίωση.
Ο Αναξαγόρας (500 περίπου π.Χ.), φιλόσοφος από τις Κλαζομενές, δέχεται ότι “όλα τα στοιχεία στην αρχή ήταν ανακατεμένα και συγκεχυμένα. Τα πάντα ήταν μέσα στα πάντα. Όλα όσα σήμερα είναι ξεχωρισμένα, αποτελούσαν μια μάζα αξεχώριστη και ηρεμούσα. Το μίγμα αυτό δεν θα έβγαινε από την ηρεμία του αν ο νους δεν έδινε σ’ αυτό την κίνηση και δεν το διαχώριζε”. Έτσι, ασχολείται με τα ασταθή, τυχαία, ανακατεμένα και συγκεχυμένα στοιχεία της πρωταρχικής άπειρης ύλης.
Στη “Γένεση” της Παλαιάς Διαθήκης “η Γη ην αόρατος και ακατασκεύαστος και σκότος εφέρετο υπεράνω της αβύσσου”.
Σ’ ένα πρώιμο βαβυλωνιακό έπος το σύμπαν γεννιέται απ’ το χάος που προκύπτει όταν μια ανυπάκουη οικογένεια Θεών της αβύσσου καταστρέφεται από τον πατέρα της. Το χάος είναι η αρχέγονη άμορφη μάζα από την οποία ο δημιουργός έπλασε την τάξη και το σύμπαν. Η τάξη ισοδυναμεί με το καλό, και η αταξία με το κακό. Η τάξη και το χάος φαίνονται σαν δύο αντίθετα πράγματα, σαν δύο πόλοι γύρω απ’ τους οποίους περιστρέφουμε τις ερμηνείες μας σχετικά με τον κόσμο.
Κάποια έμφυτη παρόρμηση κάνει την ανθρωπότητα να προσπαθεί να κατανοήσει την κανονικότητα στη φύση, να ερευνήσει τους νόμους που κρύβονται πίσω από την παράξενη πολυπλοκότητα του σύμπαντος, να βγάλει κάποια τάξη μέσα απ’ το χάος.
Στη σύγχρονη εποχή οι επιστήμονες, φυσικοί, βιολόγοι, μαθηματικοί, μηχανικοί, χημικοί και άλλοι, ερευνώντας διάφορα στοιχεία για να εξηγήσουν κάποιες αταξίες που κυριαρχούν στο χαοτικό οργανικό και ανόργανο κόσμο, οδηγούνται να βρουν τον τρόπο με τον οποίον θα μπορούσαν να μεταβάλουν σε κάθε περίπτωση τα πολύμορφα στοιχεία σε ομοιόμορφα, τα πολύπλοκα σε απλά, τα ασταθή σε σταθερά, τα τυχαία και απρόβλεπτα σε καθορισμένα.
Το Χάος σαν Επιστήμη
Σήμερα με τον όρο Χάος χαρακτηρίζεται ο κλάδος που αντικείμενο μελέτης του είναι κάποια εξαιρετικά πολύπλοκα συστήματα που η εξέλιξή τους στο χρόνο εξαρτάται ισχυρά από τις αρχικές συνθήκες υπό τις οποίες αναλύεται. Συγκεκριμένα, η Θεωρία του Χάους μελετά τη συμπεριφορά ορισμένων μη γραμμικών δυναμικών συστημάτων, τα οποία χαρακτηρίζονται κυρίως από μια ευαίσθητη εξάρτηση από τις αρχικές συνθήκες αλλά και από μια μη περιοδικότητα. Η ευαισθησία αυτή έχει ως αποτέλεσμα την φαινομενική τυχαιότητα της παρατηρούμενης συμπεριφοράς των συστημάτων, παρ’ όλο που τα συστήματα αυτά είναι αιτιοκρατικά ή ντετερμινιστικά”, με την έννοια ότι είναι καλώς ορισμένοι οι νόμοι εξέλιξής τους και δεν περιέχουν τυχαίες παραμέτρους.
Ένα μη γραμμικό δυναμικό σύστημα μπορεί, σε γενικές γραμμές, να παρουσιάζει μια ή περισσότερες από τις παρακάτω συμπεριφορές:
– να καταλήγει σε ηρεμία (ακινησία)
– να επεκτείνεται συνεχώς (μόνο για μη φραγμένα συστήματα) ή όπως λέγεται να συμβαίνει μια “έκρηξη”
– να εκτελεί περιοδική κίνηση ή ημι-περιοδική κίνηση
– να εκτελεί χαοτική κίνηση
Η συμπεριφορά που ένα σύστημα μπορεί να παρουσιάσει εξαρτάται όπως είπαμε από την αρχική του κατάσταση και τις τιμές των παραμέτρων, αν υπάρχουν. Η πιο δύσκολη στην παρατήρηση και πρόβλεψη είναι η χαοτική κίνηση, μια σύνθετη, μη περιοδική κίνηση, που έχει δώσει και το όνομά της στη θεωρία.
Η ευαισθησία στις αρχικές συνθήκες σημαίνει ότι δύο σημεία σε ένα τέτοιο σύστημα μπορούν να ακολουθήσουν ριζικά διαφορετικές τροχιές στον φασικό χώρο, ακόμα και αν η διαφορά στις αρχικές συνθήκες είναι εξαιρετικά μικρή. Τα συστήματα συμπεριφέρονται με τον ίδιο τρόπο μόνο όταν η αρχική διαμόρφωση είναι ακριβώς η ίδια. Ουσιαστικά, αυτό σημαίνει ότι χρειάζεται κανείς να προσδιορίσει τις αρχικές συνθήκες με απεριόριστη ακρίβεια, προκειμένου να προβλέψει πώς θα συμπεριφερθεί το σύστημα πέρα από έναν περιορισμένο “χρονικό ορίζοντα”. Στην πράξη μπορούμε να προσδιορίσουμε τις αρχικές συνθήκες με περιορισμένη ακρίβεια μόνο.
Η μελέτη του Χάους είναι μια νέα επιστήμη και αποτελεί την βάση μελέτης κάθε ερευνητή στη Φυσική, τη Βιολογία (εξέλιξη των πληθυσμών), τα Μαθηματικά, την Οικονομία, τη Μετεωρολογία, τη Γεωλογία (κινήσεις τεκτονικών πλακών), την Αστρονομία (το ηλιακό σύστημα) και αλλού.
Η επιστήμη του Χάους αποτελεί την τρίτη μεγάλη επανάσταση του 20ου αιώνα, μετά απ’ αυτή της κβαντομηχανικής και της σχετικότητας. Αποσκοπεί στην αποκατάσταση της τάξης και της ισορροπίας στην σύγχρονη ζωή και τη σκέψη των ανθρώπων, αφού υποτάξει με την γνώση τις ανεξέλεγκτες δυνάμεις του σύμπαντος.
Από μαθηματική άποψη η Θεωρία του Χάους μελετά τη συμπεριφορά ορισμένων μη γραμμικών δυναμικών συστημάτων, τα οποία κάτω από ορισμένες συνθήκες παρουσιάζουν χαοτική συμπεριφορά. Χαρακτηρίζεται κυρίως από ευαίσθητη εξάρτηση από τις αρχικές συνθήκες – γνωστή και ως φαινόμενο της πεταλούδας – και ακολούθως από μη περιοδικότητα. Η ευαισθησία αυτή έχει ως αποτέλεσμα την φαινομενική τυχαιότητα της παρατηρούμενης συμπεριφοράς των συστημάτων, παρ’ όλο που τα συστήματα αυτά είναι αιτιοκρατικά (“ντετερμινιστικά”), με την έννοια ότι είναι καλώς ορισμένοι οι νόμοι εξέλιξής τους και δεν περιέχουν τυχαίες παραμέτρους.
Γνωρίζουμε σήμερα ότι είναι δυνατό να έχουμε εξαιρετικά πολύπλοκη, δηλαδή χαοτική, κίνηση και συνεπώς μη προβλέψιμη, ακόμα και σε απλά δυναμικά συστήματα με δύο βαθμούς ελευθερίας, ενώ μέχρι τότε πιστεύονταν ότι άτακτη, απρόβλεπτη, κίνηση έχουμε μόνο σε πολύπλοκα συστήματα, με πολλούς βαθμούς ελευθερίας, όπως π.χ. στην κίνηση των μορίων του αέρα σε ένα δωμάτιο
Στα συστήματα αυτού του είδους περιλαμβάνονται η ατμόσφαιρα, το ηλιακό σύστημα, οι τεκτονικές πλάκες, τα οικονομικά συστήματα και η εξέλιξη (μεταβολή) των πληθυσμών.
Οι αρχαίοι Έλληνες φιλόσοφοι με την τότε αποκάλυψη της έννοιας “Χάος” θέτουν στο σύγχρονο άνθρωπο το τραγικό ερώτημα: Μήπως ο Θεός παίζει ζάρια, μήπως παίζει ένα βαθύτερο παιχνίδι που δεν έχουμε ακόμη κατανοήσει; μήπως τελικά ο άνθρωπος είναι τα “ζάρια” στα χέρια ενός ακαταμάχητου “Θεού”;
Κάτι που αρνήθηκε ο Αϊνστάιν να δεχθεί όπως τόνισε στην πολύκροτη επιστολή του προς τον Max Born για την πιθανοκρατική εξήγηση του Κβαντικού Κόσμου.
Ύστερα από χιλιάδες χρόνια ο άνθρωπος κατάλαβε ότι η Φύση υπόκειται σε πολλούς κανόνες ή νόμους. Τον 18ο αιώνα ανακαλύφθηκαν τόσοι νόμοι που οι επιστήμονες πίστεψαν πως τα ήξεραν πια όλα, και μπορούσαν να περιγράψουν όλα τα φαινόμενα με αναλλοίωτους νόμους. Έτσι, το Χάος του Ησίοδου υποχώρησε μπροστά σ’ ένα κόσμο που φαινόταν πως λειτουργούσε σαν ωρολογιακός μηχανισμός.
Πριν από δύο αιώνες περίπου ο Γάλλος μαθηματικός και αστρονόμος Laplace έγραψε την Αναλυτική του Θεωρία περί των Πιθανοτήτων. Στην αφιέρωσή του προς τον Ναπολέοντα ομολογούσε ότι με το έργο του επιδιώκει να δώσει απάντηση περί των πιο σημαντικών προβλημάτων της ζωής, τα οποία, στο μεγαλύτερο μέρος τους, δεν είναι παρά προβλήματα πιθανοτήτων. Με το έργο του αυτό ο Laplace θεωρήθηκε ως ο κύριος εκφραστής της αιτιοκρατίας, ή αλλιώς, του ντετερμινισμού. Στην εισαγωγή του έργου του υποστηρίζει ότι πρέπει να θεωρήσουμε την παρούσα κατάσταση του σύμπαντος ως το αποτέλεσμα του παρελθόντος και ταυτόχρονα ως την αιτία του μέλλοντος:
Ο κόσμος, όμως, συνέχισε την εξέλιξη του και μαζί του εξελίχτηκε και η άποψη μας για το σύμπαν. Σήμερα ακόμα και τα ρολόγια δεν λειτουργούν πια με τον τετριμμένο “ωρολογιακό” μηχανισμό — γιατί λοιπόν θα έπρεπε να λειτουργεί έτσι ο Κόσμος μας;
Με την εμφάνιση της κβαντομηχανικής, ο ωρολογιακός μηχανισμός του Κόσμου μετατράπηκε σε μια παγκόσμια ρουλέτα. Θεμελιώδη φαινόμενα, όπως η διάσπαση ενός ραδιενεργού πυρήνα, καθορίζονται από τυφλή τυχαιότητα και όχι από αυστηρή νομοτέλεια. Αλλά, παρά τη θεαματική επιτυχία που είχε η κβαντομηχανική, τα πιθανολογικά της χαρακτηριστικά δεν έπεισαν τους πάντες. Η περίφημη αντίρρηση του Αϊνστάιν προς τον Max Born αναφερόταν στην κβαντομηχανική, αλλά η φιλοσοφία του προσέγγιζε επίσης τη στάση μιας ολόκληρης εποχής απέναντι στην κλασική μηχανική, όπου η απροσδιοριστία του κβάντου δεν ισχύει. Η παρομοίωση των ζαριών με το τυχαίο αφορά όλη την επιστήμη.
Μήπως όμως αφήνει χώρο το νομοτελειακό και για το τυχαίο;
Σήμερα ξέρουμε ότι ο κόσμος της κλασικής μηχανικής είναι ασφαλώς πιο μυστηριώδης απ’ όσο φανταζόταν κι ο ίδιος ο Αϊνστάιν. Η διάσταση που προσπαθούσε να τονίσει ανάμεσα στην απροσδιοριστία του τυχαίου και στην απόλυτη βεβαιότητα του νόμου, έχει τεθεί υπό αμφισβήτηση. Ίσως ο Θεός παίζοντας ζάρια, δημιουργεί με την ίδια κίνηση ένα σύμπαν πλήρους νομοτέλειας και τάξης.
Ο κύκλος ολοκλήρωσε την περίοδο του, αλλά σ’ ένα υψηλότερο επίπεδο. Αρχίζουμε ν’ ανακαλύπτουμε ότι συστήματα που υπακούουν σε σταθερούς και ακριβείς νόμους δεν δρουν πάντα με κανονικό τρόπο, που μπορεί να προβλεφθεί. Απλοί νόμοι μπορεί να μην οδηγούν σε απλή συμπεριφορά. Ντετερμινιστικοί νόμοι μπορούν και παράγουν συμπεριφορά που να μοιάζει τυχαία. Η τάξη μπορεί να γεννά ένα δικό της είδος χάους. Το ερώτημα δεν είναι τόσο αν πράγματι ο Θεός ρίχνει τα ζάρια, αλλά το πώς τα ρίχνει.
Αυτή είναι μια δραματική ανακάλυψη, οι συνέπειες της οποίας δεν έχουν ακόμη δώσει την πληρότητα της πρόκλησης στην επιστημονική μας σκέψη. Οι έννοιες της πρόβλεψης, ή ενός πειράματος που επαναλαμβάνεται κανονικά, αποκτούν νέα όψη όταν τα κοιτάξουμε με τα μάτια του χάους. Αυτό που νομίζαμε απλό, γίνεται περίπλοκο και νέα ενοχλητικά ερωτήματα προβάλλουν όσον αφορά τη μέτρηση, την προβλεψιμότητα και την επαλήθευση ή τη διάψευση θεωριών.
Σαν αντιστάθμισμα, αυτό που θεωρήθηκε κάποτε περίπλοκο μπορεί να καταστεί απλό. Φαινόμενα που μοιάζουν τυχαία και χωρίς δομή, μπορεί τελικά να υπακούουν σε απλούς νόμους. Το ντετερμινιστικό χάος έχει κι αυτό τους δικούς του νόμους και εμπνέει νέες τεχνικές πειραματισμού. Υπάρχει πλήθος αταξιών στη φύση, ορισμένες από τις οποίες μπορεί ν’ αποδειχθούν φυσιολογικές εκδηλώσεις των μαθηματικών του χάους. Η στροβιλώδης ροή των ρευστών, οι αναστροφές στο μαγνητικό πεδίο της Γης, οι αρρυθμίες των χτύπων της καρδιάς, ο τρόπος μεταφοράς θερμότητας από το υγρό ήλιον, η μπερδεμένη διάταξη των ουράνιων σωμάτων, τα κενά στη ζώνη των αστεροειδών, η αύξηση του πληθυσμού των εντόμων, οι σταγόνες που πέφτουν από μια βρύση, η διαδικασία μιας χημικής αντίδρασης, ο μεταβολισμός των κυττάρων, οι μεταβολές του καιρού, η μετάδοση των νευρικών διεγέρσεων, οι ταλαντώσεις των ηλεκτρονικών κυκλωμάτων, η κίνηση ενός αγκυροβολημένου πλοίου, η αναπήδηση και η ανάκλαση μιας μπάλας μπιλιάρδου, οι συγκρούσεις μεταξύ των ατόμων σ’ ένα αέριο, το υπόβαθρο αβεβαιότητας της κβαντομηχανικής — να μερικά μόνο από τα, προβλήματα στα οποία έχουν εφαρμοστεί τα μαθηματικά του χάους.
Το χάος είναι ένας ολότελα καινούργιος κόσμος, ένα νέο είδος μαθηματικών, μια θεμελιώδης καινοτομία στην κατανόηση της αταξίας στη φύση. Κι εμείς είμαστε μάρτυρες στη γέννηση αυτής της επιστήμης. Η οποία έχει μεγάλο μέλλον μπροστά της.
Αναδύεται η Τάξη μέσα από τους Νόμους του Νεύτωνα
Ο Ισαάκ Νεύτωνα πριν 300 τόσα χρόνια έγραψε το “Οι Μαθηματικές Αρχές της Φυσικής Φιλοσοφίας”. Το μήνυμα του βιβλίου του είναι ότι η Φύση έχει νόμους. Και τους νόμους αυτούς μπορούμε να τους ανακαλύψουμε.
Για περισσότερο από δυο αιώνες οι νόμοι του Νεύτωνα κυριαρχούσαν ως η απόλυτη περιγραφή της φύσης. Μόνο στη μικροσκοπική περιοχή του ατόμου και στην τεράστια έκταση του διαστρικού χώρου έχουν γίνει γνωστές κάποιες διαφορές ανάμεσα στη Φύση σύμφωνα με το Νεύτωνα και στη φύση της Φύσης, Σ’ αυτές τις περιοχές η θεωρία του Νεύτωνα έχει τώρα αντικατασταθεί από την κβαντομηχανική και τη θεωρία της σχετικότητας.
Η επανάσταση στην επιστημονική σκέψη που κορυφώθηκε με το Νεύτωνα, οδήγησε στη θεώρηση του σύμπαντος ως ενός γιγαντιαίου μηχανισμού που λειτουργεί “σα ρολόι”, μια μεταφορική φράση που χρησιμοποιούμε για να αποδώσουμε τη μέγιστη αξιοπιστία και τη μηχανική τελειότητα — αν και είναι πια κάπως άστοχη στη σημερινή εποχή των ψηφιακών ρολογιών.
Σε μια τέτοια θεώρηση, η λειτουργία μιας τέτοιας Μηχανής είναι πέρα για πέρα προβλέψιμη. Κάτω από ταυτόσημες συνθήκες κάνει ταυτόσημα πράγματα. Ένας μηχανικός που γνωρίζει τα χαρακτηριστικά μιας μηχανής και την κατάσταση της σε κάθε στιγμή, μπορεί, θεωρητικά, να υπολογίζει τη μελλοντική της λειτουργία.
Μολονότι παρουσιάζονται διάφορες δυσκολίες κατά την επίλυση των διαφορικών εξισώσεων στην κίνηση των σωμάτων, μπορούν να καθιερωθούν ορισμένες γενικές αρχές. Η αρχή – κλειδί είναι ότι η λύση των εξισώσεων που περιγράφουν την κίνηση ενός δυναμικού συστήματος είναι μοναδική αν οι αρχικές θέσεις και ταχύτητες όλων των συστατικών του συστήματος είναι γνωστές. Για παράδειγμα: αν σε κάποια δεδομένη στιγμή γνωρίζουμε τις θέσεις και τις ταχύτητες κάθε υλικού σωματιδίου στο Ηλιακό Σύστημα, τότε μπορούμε να προσδιορίσουμε με μοναδικό τρόπο όλες τις επακόλουθες κινήσεις αυτών των σωματιδίων.
Αυτή η πρόταση δέχεται, χάριν απλότητας, ότι δεν υπάρχουν εξωτερικές επιδράσεις πάνω στην κίνηση. Αν υπολογίζαμε και αυτές τις επιδράσεις, θα οδηγούμασταν στο συμπέρασμα ότι οι θέσεις και οι ταχύτητες όλων των υλικών σωματιδίων που υπάρχουν σ’ ολόκληρο το σύμπαν, δεδομένες σε μια ορισμένη χρονική στιγμή, καθορίζουν απόλυτα τη μελλοντική του εξέλιξη. Το σύμπαν ακολουθεί μια μοναδική, προκαθορισμένη πορεία. Μπορεί να κάνει ένα μόνο πράγμα.
Όπως εύγλωττα αναφέρει ο (Pierre Simon de Laplace ή Λαπλάς, ένας από τους κορυφαίους μαθηματικούς του 18ου αιώνα, στο βιβλίο του Φιλοσοφικά Δοκίμια επί των πιθανοτήτων:
Αν υπήρχε μια Νόηση που να γνώριζε σε κάθε στιγμή όλες τις δυνάμεις που δίνουν κίνηση στη Φύση και τις σχετικές θέσεις όλων των πραγμάτων που υπάρχουν σ’ αυτή, κι αν αυτή η Νόηση Ι ήταν τέτοια ώστε να κατορθώσει ν’ αναλύσει τα δεδομένα, θα μπορούσε να συνοψίσει σ’ ένα μοναδικό τύπο την κίνηση των μεγαλύτερων σωμάτων του σύμπαντος μαζί μ’ αυτή των ελαφρύτερων ατόμων: για μια τέτοια Νόηση τίποτα δεν θα ήταν αβέβαιο. Και το μέλλον, όπως επίσης και το παρελθόν, θα γινόταν παρόν μπροστά στα μάτια της.
Αυτή είναι μάλλον μια τοποθέτηση που προκαλεί δέος καθώς προκύπτει από ένα απλό θεώρημα μοναδικότητας στα μαθηματικά. Μερικά όμως από τα παραπάνω είναι όπως ξέρουμε σήμερα πραγματικά υπερβολικά και δεν ισχύουν. Για την ώρα, ας δεχτούμε ότι αυτή η ερμηνεία για τον κόσμο ευσταθεί. Η θέση του Λαπλάς είχε τέτοια επιρροή στην επιστήμη που εφαρμοζόταν σε όλα τα φαινόμενα — μηχανική, θερμότητα, κύματα, ήχος, φως, μαγνητισμός, ηλεκτρισμός. Θα πρέπει να φαινόταν σαν η μεγάλη διείσδυση στην έσχατη αλήθεια. Και πέτυχε. Το πρότυπο του κλασικού ντετερμινισμού είχε γεννηθεί: αν οι εξισώσεις προδιαγράφουν την εξέλιξη του συστήματος με τρόπο μοναδικό, χωρίς τυχαίες εξωτερικές επιδράσεις, τότε η συμπεριφορά του συστήματος είναι προκαθορισμένη.
Η χαοτική κίνηση του Υπερίωνα
Στις 5 Σεπτεμβρίου 1977 εκτοξεύτηκε ένα ιστορικό διαστημόπλοιο, ο Voyager 1, που είχε σαν στόχο τους εξωτερικούς πλανήτες Άρη, Δία και Κρόνο.
Ο μαθηματικός νόμος που κυβερνά όλους τους πλανήτες και τα φεγγάρια τους είναι ο νόμος βαρύτητας του Νεύτωνα. Η θεωρία της σχετικότητας του Αϊνστάιν δεν χρειάζεται να εφαρμοστεί εδώ – αντί για το Νόμο Του Νεύτωνα – γιατί οι ταχύτητες τους είναι πολύ μικρότερες από την ταχύτητα του φωτός. Βέβαια οι υπολογισμοί είναι πολύ χρονοβόροι και δύσκολοι, γιατί δεν έχουμε μόνο την αλληλεπίδραση μόνο της Γης και του Ήλιου, αλλά τις αλληλεπιδράσεις συγχρόνως πολλών ουρανίων σωμάτων.
Χρησιμοποιώντας τους μαθηματικούς νόμους του Νεύτωνα, οι αστρονόμοι έχουν προβλέψει την κίνηση του Ηλιακού Συστήματος για πάνω από 200 εκατομμύρια χρόνια — έτσι οι υπολογισμοί για τα λίγα χρόνια που κρατούσε το ταξίδι του Voyager 1 δεν ήταν πρόβλημα.
Πέρα από τον Δία υπάρχει ο Κρόνος στον οποίο δεσπόζουν οι δακτύλιοι και τα πολλά φεγγάρια. Ένας δορυφόρος του Κρόνου, ο Υπερίωνας, είναι ασυνήθιστος. Έχει ανώμαλο σχήμα, σαν μια κοσμική πατάτα. Η τροχιά του είναι ακριβής και κανονική, αλλά η συμπεριφορά του στην τροχιά δεν είναι. Ο Υπερίωνας κάνει τούμπες. Όχι με το “κεφάλι” προς τα κάτω, αλλά μ’ ένα περίπλοκο και ακανόνιστο τρόπο. Τίποτα ωστόσο σ’ αυτή την παράξενη συμπεριφορά δεν αντικρούει τους νόμους του Νεύτωνα. Και οι τούμπες του Υπερίωνα υπακούουν στους νόμους της βαρύτητας και της δυναμικής.
Έστω ότι ο Voyager 1 είχε υπολογίσει τις ‘τούμπες’ του Υπερίωνα με ακρίβεια δέκα δεκαδικών ψηφίων και πάνω σ’ αυτή τη βάση οι επιστήμονες στη Γη έκαναν την καλύτερη δυνατή πρόβλεψη για τη μελλοντική κίνηση του Υπερίωνα, σύμφωνα με το νόμο του Νεύτωνα. Τότε, ύστερα από λίγους μήνες όταν ένα άλλο διαστημόπλοιο, ο Voyager 2, θα περνούσε από τον Υπερίωνα, θα μπορούσαν να συγκρίνουν τις αριθμητικές προβλέψεις τους με την πραγματικότητα.
Θα έβλεπαν λοιπόν ότι η πρόβλεψη για την τροχιά του Υπερίωνα ήταν εντελώς λανθασμένη.
Μήπως υπήρχε λάθος στην πρόβλεψη;
Όχι ακριβώς.Οφείλεται σε μια αποτυχία του νόμου του Νεύτωνα;
Όχι. Η πρόβλεψη αναμένεται να είναι λανθασμένη, εξαιτίας του νόμου του Νεύτωνα.Ανυπαρξία νομοτέλειας; Τυχαίοι εξωγενείς παράγοντες, όπως νεφελώδη αέρια, μαγνητικά πεδία, ο ηλιακός άνεμος;
Όχι.
Κάτι πολύ πιο αξιοσημείωτο. Ένα σύμφυτο χαρακτηριστικό των μαθηματικών εξισώσεων στη δυναμική. Η δυνατότητα ακόμα και απλών εξισώσεων να παράγουν κίνηση τόσο περίπλοκη, τόσο ευαίσθητη στις αρχικές συνθήκες, ώστε να φαίνεται τυχαία. Η σωστή ονομασία της είναι χάος.
Χάος
Αλλά τι είναι Χάος; Τα λεξικά λένε ότι το Χάος είναι τρία πράγματα:
1. Η άτακτη, άμορφη ύλη που υποτίθεται ότι προϋπήρχε του εννόμου σύμπαντος (όπως λένε οι αρχαίες κοσμογονίες)
2. Απόλυτη αταξία, πλήρης σύγχιση (όπως το καταλαβαίνουν οι άνθρωποι στην καθημερινή ζωή τους).
3. Στοχαστική συμπεριφορά που εκδηλώνεται σ’ ένα ντετερμινιστικό σύστημα (ένας φυσικο-μαθηματικός ορισμός)
Τι σημαίνουν όμως “στοχαστική συμπεριφορά” και “ντετερμινιστικό σύστημα”. Η αιτιοκρατία ή ντετερμινισμός του Λαπλάς μας είναι ήδη γνωστός. “Στοχαστικό” σημαίνει “τυχαίο”. Για να καταλάβουμε το φαινόμενο του χάους θα χρειαστεί να συζητήσουμε περισσότερο τις σημασίες αυτών των δύο λέξεων, γιατί ο τρόπος που χρησιμοποιούνται στον ορισμό φαίνεται παράλογος. Η νομοτελειακή συμπεριφορά υπακούει σ’ έναν ακριβή και άρρηκτο νόμο. Η στοχαστική συμπεριφορά είναι το αντίθετο: Δεν έχει ούτε νόμους ούτε τάξη, και καθοδηγείται απ’ το τυχαίο. Άρα, το χάος είναι “μια συμπεριφορά χωρίς τάξη που όμως καθοδηγείται ολοκληρωτικά από κάποιο νόμο”. Όπως ο Υπερίωνας.
Γιατί ο Υπερίωνας συμπεριφέρεται τελικά μ’ αυτόν τον τρόπο; Δεν είναι ακόμη εύκολο να το πούμε, αλλά υπάρχει ένα παράδειγμα του χάους με το οποίο μπορείτε να πειραματιστείτε και οι ίδιοι. Χρειάζεστε μόνο μια αριθμομηχανή τσέπης. Αν έχετε στο σπίτι έναν υπολογιστή μπορείτε εύκολα να τον προγραμματίσετε να κάνει την ίδια δουλειά και να γλιτώσετε οι ίδιοι από πολύ κόπο.
Η εξίσωση που ελέγχει την κίνηση του Υπερίωνα είναι μια διαφορική εξίσωση. Ας υποθέσουμε ότι σε μια δεδομένη στιγμή, γνωρίζουμε τη θέση και την ταχύτητα του Υπερίωνα. Τότε υπάρχει ένας σταθερός νόμος που εφαρμόζουμε σ’ αυτά τα δεδομένα για να πάρουμε τη θέση και την ταχύτητα κατά την επόμενη χρονική στιγμή. Εφαρμόζουμε λοιπόν και πάλι το νόμο, και συνεχίζουμε με αυτό τον τρόπο ώσπου να φτάσουμε στο χρονικό σημείο που θέλουμε.
Για να λύσει τη διαφορική εξίσωση ένας υπολογιστής χρησιμοποιεί πολύ μικρά βήματα. Η μέθοδος πετυχαίνει γιατί τα πολύ μικρά χρονικά βήματα δίνουν μια καλή προσέγγιση της συνεχούς ροής του χρόνου.
Οι εξισώσεις για τον Υπερίωνα περιλαμβάνουν πολλές μεταβλητές — θέση, ταχύτητα, μεταβολή προσανατολισμού. Θα μπορούσατε να τις βάλετε στον υπολογιστή σας, αλλά θέλετε πολύ χρόνο. Αντί γι’ αυτές θα επιλέξουμε μια πολύ απλούστερη εξίσωση, η οποία δεν έχει καμιά σχέση με την κίνηση του Υπερίωνα, επεξηγεί, όμως, το φαινόμενο του χάους.
Ας πάρουμε την συνάρτηση f(x)=x2-1. Βάζοντας στη θέση του x για αρχή το 0 παίρνουμε f(0)=-1, κι αν βάλουμε στη θέση του x το προηγούμενο αποτέλεσμα, το -1, τότε παίρνουμε f(-1)=0. Η επαναληπτική εφαρμογή της συνάρτησης x2-1 οδηγεί σε μια κυκλική εναλλαγή του 0 και του -1, δηλαδή μια κανονική ταλάντωση.
Πάνω: Η τιμή του x (ο και -1) σημειώνεται στην κατακόρυφη διεύθυνση, ενώ ο αριθμός των επαναλήψεων στην οριζόντια διεύθυνση.
Αν πάρουμε τώρα την συνάρτηση f(x)=2x2-1, που είναι λίγο διαφορετική από την προηγούμενη . Βάζοντας στη θέση του x ένα τυχαίο αριθμό ανάμεσα στο το 0 και το 1, πχ x=0,54321 παίρνουμε μια τιμή για τη συνάρτηση. Συνεχίζουμε βάζοντας στη θέση του x την προηγούμενη τιμή (-0,4098457), και ούτω καθεξής. Η επαναληπτική εφαρμογή του 2x2-1 βλέπουμε να οδηγεί όχι σε μια κυκλική συγκεκριμένη διάταξη (όπως πριν), αλλά σε μια χαοτική ταλάντωση.
Η επαναληπτική εφαρμογή του 2x2-1 οδηγεί στο χάος
Αν βάλουμε στην ίδια συνάρτηση σαν αρχική τιμή το x=0,54321. Τότε, φαίνεται ακόμη τυχαίο — και μετά από πενήντα περίπου επαναλήψεις και πάλι φαίνεται τελείως διαφορετικό.
Αυτό που βλέπετε είναι ένα είδος Υπερίωνα μέσα στο μικρόκοσμο. Ντετερμινιστική εξίσωση: αόριστο αποτέλεσμα. Ανεπαίσθητη αλλαγή στην αρχική τιμή: χάνονται τελείως τα ίχνη για το πού πηγαίνει. Αυτό που το κάνει πιο αξιοσημείωτο είναι ότι ενώ το 2x2-1, είναι τόσο παράξενο, η επιφανειακά παρόμοια συνάρτηση x2-1 συμπεριφέρεται τέλεια.
Ας πάρουμε τώρα την συνάρτηση f(x)=kx2-1 με k=1.4. Εδώ γίνεται μια αρκετά πολύπλοκη κυκλική εναλλαγή μέσ’ από δεκαέξι διαφορετικές τιμές!
Για k=1,5 δεν υπάρχει καμιά κυκλική εναλλαγή τιμών, αλλά χάος. Συνεχίζουμε με k=1,75 και βλέπουμε ότι αρχικά για 50 περίπου επαναλήψεις βλέπουμε χάος. Όμως, μετά από 50 περίπου επαναλήψεις σταθεροποιείται σ’ έναν κύκλο με τρεις μόνο αριθμούς, μια επανάληψη γύρω στους αριθμούς :0,744 -0,030 -0,998.
Αυτό που έχουμε ανακαλύψει είναι ένα θαύμα. Τάξη και χάος, στενά συνδεδεμένα, αναδύονται από έναν τύπο τόσο απλό όπως οkx2-1. Ορισμένες τιμές οδηγούν σε επαναλήψεις που εμφανίζουν τάξη, άλλες — ελάχιστα διαφορετικές — οδηγούν στο χάος.
Μέσα από το αρχικό χάος λοιπόν αναδύεται τάξη! Τα δύο αυτά είναι συνδεδεμένα μ’ έναν τρόπο ανεξιχνίαστο και μυστηριώδες.
Ας δούμε τώρα κάτι σχετικά με τους υπολογιστές και το χάος. Έχουμε την τάση να σκεφτόμαστε τους υπολογιστές σαν ιδεώδη παραδείγματα ακρίβειας. Στην πραγματικότητα δεν είναι. Οι περιορισμοί της μνήμης συνεπάγονται ότι οι αριθμοί συγκρατούνται από τον ηλεκτρονικό υπολογιστή με πολύ περιορισμένη ακρίβεια, ας πούμε με οκτώ ή δέκα δεκαδικά ψηφία. Επιπλέον, ο “ιδιωτικός” εσωτερικός κώδικας — που χρησιμοποιεί ο υπολογιστής για να αναπαραστήσει μέσα του τους αριθμούς — και ο “κοινός” με τον οποίο τους εκτυπώνει στην οθόνη, είναι διαφορετικοί. Η διαφορά αυτή οδηγεί σε δύο πηγές λαθών. Λάθος κατά τη στρογγυλοποίηση στους εσωτερικούς υπολογισμούς, και λάθος κατά την απόδοση από τον ιδιωτικό κώδικα στον κοινό. Συνήθως αυτά τα λάθη δεν ενοχλούν πολύ, ένα όμως από τα χαρακτηριστικά γνωρίσματα του χάους είναι ότι ευνοεί την ανάπτυξη και αναπαραγωγή τέτοιων μικρών λαθών.
Στοχαστική και Χάος
Η λέξη “gas” επινοήθηκε από τον Ολλανδό χημικό Van Helmont στο βιβλίο του Ortus Medicinae, το 1632 μ’ εσκεμμένη ομοιότητα προς την ελληνική λέξη “χάος” (chaos). Ήταν μια πολύ οξυδερκής επιλογή. Στη φυσική των αερίων έρχονται αμέσως αντιμέτωπα το τυχαίο και το ντετερμινιστικό. Στην ουσία όμως, ένα αέριο είναι μια ντετερμινιστική συνάθροιση κινουμένων μορίων που υπακούουν σε ακριβείς δυναμικούς νόμους. Από πού λοιπόν προέρχεται το τυχαίο;
Η απάντηση — που θα έδινε αυτόματα κάθε αξιόλογος επιστήμονας ως τη δεκαετία του 70 και πολλοί ακόμα και στις αρχές της δεκαετίας του ’80 — λέγεται πολυπλοκότητα. Η λεπτομεριακή κίνηση του αερίου είναι πολύ σύνθετη για να την κατανοήσουμε.
Ας υποθέσουμε ότι έχουμε μια συσκευή ικανή να παρακολουθεί ένα λογικό αριθμό ξεχωριστών μορίων αερίου καθώς κινούνται. Δεν υπάρχει τέτοια συσκευή, αλλά και αν υπήρχε, θα ‘πρεπε να χρησιμοποιήσουμε υπολογιστή για να επιβραδύνει την κίνηση κατά πολλές τάξεις μεγέθους ώστε να δούμε τι συμβαίνει. Ας υποθέσουμε όμως ότι γίνεται. Τι θα βλέπαμε; Ας συγκεντρώσουμε την προσοχή μας σε μια μικρή ομάδα μορίων. Τα μόρια ακολουθούν για μικρό χρονικό διάστημα ευθύγραμμες πορείες, ύστερα αρχίζουν να συγκρούονται μεταξύ τους και να κινούνται σε καινούργιες κατευθύνσεις τις οποίες μπορούμε να προδιαγράψουμε με βάση την προηγούμενη γεωμετρία των κατευθύνσεων τους.
Μόλις όμως έχουμε αρχίσει να καταλαβαίνουμε το μοντέλο της κίνησης, ένα νέο μόριο ορμά “ακάθεκτο” απέξω και εισβάλλει στην όμορφα οργανωμένη ομάδα μας, καταστρέφοντας το μοντέλο. Και πριν προλάβουμε να μελετήσουμε το νέο μοντέλο, έρχεται ένα άλλο μόριο κι άλλο κι άλλο…
Αν αυτό που βλέπουμε είναι ένα μικρό μέρος μιας εξαιρετικά πολύπλοκης κίνησης, τότε όλα φαίνονται τυχαία. Όλα μοιάζουν χωρίς δομή.
Με λίγα λόγια, πρόκειται για τον ίδιο μηχανισμό που κάνει τις κοινωνικές επιστήμες τόσο δύσκολες. Δεν μπορούμε να μελετήσουμε μια ζωντανή οικονομία ή ένα έθνος ή έναν εγκέφαλο, με το ν’ απομονώνουμε ένα μικρό μέρος.
Το πειραματικό μας υποσύστημα θα διαταράσσεται διαρκώς από απροσδόκητες και ανεξέλεγκτες επιδράσεις. Ακόμα και στις φυσικές επιστήμες το μεγαλύτερο μέρος της καθημερινής πειραματικής δουλειάς αφιερώνεται στην προσπάθεια για ελαχιστοποίηση των εξωτερικών επιδράσεων.
Ένας ευαίσθητος σεισμογράφος δεν θα καταγράψει μόνο τον σεισμό, αλλά και την κίνηση του φορτηγού στον δρόμο. Οι φυσικοί φτάνουν στα απώτατα άκρα για να ελαττώσουν τέτοιες ανεπιθύμητες επιδράσεις. Τοποθετούν τηλεσκόπια σε κορφές βουνών και όχι στους ουρανοξύστες του Manhattan, θάβουν μετρητές νετρίνων χιλιόμετρα κάτω απ’ το έδαφος αντί να τους τοποθετήσουν στο γραφείο.
Ο κοινωνιολόγος όμως, δεν έχει ούτε αυτή την πολυτέλεια. Πρέπει να χρησιμοποιήσει στατιστικές μεθόδους για να προκαθορίσει ή να απαλείψει αυτές τις εξωτερικές επιδράσεις. Η στατιστική είναι η μέθοδος για να κοσκινίζουμε την πολύτιμη τάξη μέσ’ από την άμμο της πολυπλοκότητας.
Οι επιστήμονες από εκατοντάδες κιόλας χρόνια, γνώριζαν καλά ότι είναι πιθανόν ένα ντετερμινιστικό σύστημα να συμπεριφερθεί μ’ έναν φαινομενικά τυχαίο τρόπο. Αλλά γνώριζαν ότι δεν ήταν αληθινά τυχαίος, απλώς έδειχνε έτσι, λόγω έλλειψης στοιχείων. Γνώριζαν ακόμα ότι αυτό το “απατηλό τυχαίο” συνέβαινε μόνο σε πολύ μεγάλα και σύνθετα συστήματα — συστήματα με εξαιρετικά πολλούς βαθμούς ελευθερίας, με εξαιρετικά πολλές διαφορετικές μεταβλητές και με εξαιρετικά πολλά συστατικά μέρη. Συστήματα των οποίων η λεπτομερειακή συμπεριφορά θα έμενε για πάντα έξω από τις δυνατότητες του ανθρώπινου μυαλού.
Κατά την διάρκεια του 20ου αιώνα, η στατιστική μεθοδολογία πήρε τη θέση της, σαν ισάξιος συμβαλλόμενος, δίπλα στη ντετερμινιστική προτυποποίηση. Μια νέα λέξη πλάστηκε για να εκφράσει τη συνειδητοποίηση ότι ακόμα και το τυχαίο έχει τους νόμους του: η λέξη στοχαστικό. Η Ελληνική λέξη στοχαστικός σημαίνει “ο ικανός στη σκόπευση”, και έτσι αποδίδει το νόημα της χρησιμοποίησης, των νόμων του τυχαίου προς κάποια ωφέλιμη κατεύθυνση.
Τα μαθηματικά των στοχαστικών ανελίξεων — της αλληλουχίας αποτελεσμάτων που καθορίζονται από την επίδραση του τυχαίου — άνθισαν παράλληλα με τα μαθηματικά των ντετερμινιστικών ανελίξεων.
Η τάξη δεν ήταν πια συνώνυμη με το νόμο, ούτε και η αταξία συνώνυμη με την απουσία νόμου. Και η τάξη και η αταξία είχαν νόμους. Αλλά νόμους που ήταν δύο διαφορετικοί κώδικες συμπεριφοράς. Άλλος νόμος για το τακτικό, άλλος για το άτακτο. Δύο πρότυπα, δύο τεχνικές. Δύο τρόποι ενόρασης του κόσμου. Δύο μαθηματικές ιδεολογίες που η κάθε μία εφαρμόζεται μόνο μέσα στη δική της σφαίρα επιρροής. Ο ντετερμινισμός γι’απλά συστήματα με λίγους βαθμούς ελευθερίας, η στατιστική για πολύπλοκα συστήματα με πολλούς βαθμούς ελευθερίας. Ένα σύστημα ή ήταν τυχαίο, ή δεν ήταν. Αν ήταν τυχαίο, οι επιστήμονες έψαχναν για κάτι στοχαστικό. Αν όχι, ξεσκόνιζαν τις ντετερμινιστικές τους εξισώσεις.
Έχουμε τελικά ένα πολύ δύσκολο ερώτημα. Είναι δυνατόν ένα απλό ντετερμινιστικό σύστημα να λειτουργήσει σαν τυχαίο σύστημα; Και μόνο το ερώτημα έρχεται σε αντίθεση με την κοινή διαίσθηση.
Η όλη εξέλιξη της επιστήμης βασιζόταν στην πεποίθηση ότι για ν’ ανιχνεύσουμε την απλότητα στη φύση πρέπει να βρούμε απλές εξισώσεις που να την περιγράφουν. Τι απλοϊκή αντίληψη!
Poincare: Ο πατέρας του Χάους
Στο σημείο αυτό της Ιστορίας, μόνο μια αντίθετη φωνή ακούστηκε, του Poincare, κι αυτή ήταν μια αχνή, αβέβαιη, διστακτική νύξη για μελλοντικά προβλήματα, μια φωνή που υψώθηκε μόνο μια φορά και μετά σιώπησε. Μια φωνή που — κι αν κάποτε ακούστηκε — αγνοήθηκε. Ηταν η φωνή ενός ανθρώπου που αναντίρρητα υπήρξε ο σπουδαιότερος μαθηματικός της εποχής του, άλλος ένας ριζοσπάστης της πολυτάραχης επιστήμης της δυναμικής. Δημιούργησε ένα ολοκληρωτικά καινούργιο πεδίο στα μαθηματικά σαν ένα παραπροϊόν. Ήταν η φωνή ενός ανθρώπου που άγγιξε το χάος…. Κι ένιωσε τρόμο.
Στα τέλη του 19ου αιώνα ο Γάλλος μαθηματικός και αστρονόμος Henri Poincare (1854 – 1912), έκανε μια ανακάλυψη που έμελλε να αλλάξει τα θεμέλια της Νευτώνιας μηχανικής, και να αποτελέσει έτσι τη γέννηση ενός νέου κλάδου της επιστήμης: του Χάους.
Συγκεκριμένα ο Poincare διαπίστωσε πως το πρόβλημα των τριών σωμάτων (μελέτησε το πρόβλημα του Ήλιου, της Γης και της Σελήνης) ήταν και παραμένει άλυτο. Άρα, δεν μπορεί να προβλεφθεί η τροχιά οποιουδήποτε ουράνιου σώματος που δέχεται την επίδραση δύο η περισσοτέρων άλλων σωμάτων. Η προσπάθεια λοιπόν να υπολογιστεί η τροχιά πχ του Πλούτωνα, δεν είναι δυνατή, αφού δέχεται την επίδραση του ήλιου και άλλων οκτώ πλανητών.
Ο Poincare αποκάλυψε το χάος στο Ηλιακό σύστημα και μαζί ανακάλυψε την απρόβλεπτη εξέλιξη ενός μη γραμμικού συστήματος. Είχε κατανοήσει πως πολύ μικρές επιδράσεις μπορούν να μεγεθυνθούν μέσω της ανάδρασης. Γι’ αυτό και διατύπωσε την άποψη “Μια ελάχιστη αιτία που διαφεύγει της προσοχής μπορεί να προκαλέσει ένα σημαντικό αποτέλεσμα”.
Η γέννηση του χάους και του απρόβλεπτου ήταν γεγονός. Αλλά χρειάστηκε να περάσουν 80 χρόνια απο τότε για να συνειδητοποιήσουν οι αστρονόμοι και οι υπόλοιποι επιστήμονες τη σπουδαιότητα αυτής της ανακάλυψης. Το 1954 πρώτος την κατανόησε ο σοβιετικός επιστήμονας A.Kolmogorov και ακολούθησαν και άλλοι.
Ο πρώτος όμως που διέκρινε πως η επανάληψη (iteration) γεννά το χάος, ανήκει στον Αμερικανό μετεωρολόγο Edward Lorenz που εργαζόταν στο MIT. Στα μέσα του χειμώνα 1961, εργαζόταν στον υπολογιστή του ΜΙΤ για να λύσει μερικές μη γραμμικές εξισώσεις που περιέγραφαν το μοντέλο της γήινης ατμόσφαιρας.
Κάποια ημέρα για να ελέγξει μια πρόγνωση που είχε πάρει από τον υπολογιστή, ξαναέδωσε τα δεδομένα του για τη θερμοκρασία, την ατμοσφαιρική πίεση και τη διεύθυνση του ανέμου αλλά αυτή τη φορά με στρογγυλοποιημένους αριθμούς. Και περίμενε να του βγάλει ο υπολογιστής την ίδια πρόγνωση. Το αποτέλεσμα όμως τον σόκαρε. Τα νέα αποτελέσματα ήταν τελείως διαφορετικά. Αμέσως κατάλαβε πως η μεγένθυση των διαφορών οφείλεται στο συνδυασμό μη γραμμικότητας και επανάληψης. Για την ιστορία, αναφέρουμε πως αντί να βάλει τον αριθμό 0.506127 με έξι δεκαδικά ψηφία, έβαλε 0.506. Από μία άποψη ήταν απόλυτα λογική σκέψη.
Στην εικόνα φαίνεται μια εκτύπωση που πήρε ο Lorenz το 1961. Από το ίδιο σημείο εκκίνησης ο Lorenz είδε τον καιρό που έδινε ο υπολογιστής της IBM να δημιουργεί σχήματα που εξελίσσονταν όλο και πιο διαφορετικά μέχρι που κάθε ομοιότητα εξαφανίστηκε.
Στον ίδιο, τον Lorenz οφείλεται και η θεωρία για την πεταλούδα που πετάει στο Χονγκ-Κονγκ και μπορεί να δημιουργήσει καταιγίδα στη Νέα Υόρκη. Ξαφνικά οι επιστήμονες συνειδητοποίησαν πως σε αιτιοκρατικά δυναμικά συστήματα, η δυνατότητα γέννησης του χάους (μη προβλεψιμότητας) παραμονεύει σε κάθε λεπτομέρεια. Και όπως έλεγε ο Lorenz: Κάθε φυσικό σύστημα που συμπεριφέρεται με μη περιοδικό τρόπο δεν είναι προβλέψιμο.
Ελκυστές
Ένας τρόπος να παρουσιάσουμε οπτικά την χαοτική κίνηση ή οποιαδήποτε άλλη κίνηση, είναι η κατασκευή ενός διαγράμματος φάσης της κίνησης. Σε ένα τέτοιο διάγραμμα υπεισέρχεται σιωπηρά ο χρόνος και σε κάθε άξονα αναπαρίσταται μια μεταβλητή της κατάστασης. Για παράδειγμα, θα μπορούσε κάποιος να αναπαραστήσει την θέση ενός εκκρεμούς σε σχέση με την ταχύτητά του. Ένα εκκρεμές σε ακινησία θα σχεδιαστεί ως ένα σημείο και ένα σε περιοδική κίνηση θα σχεδιαστεί ως απλή κλειστή καμπύλη. Όταν ένα τέτοιο σχέδιο σχηματίζει κλειστή καμπύλη, η καμπύλη λέγεται τροχιά. Το εκκρεμές μπορεί να παρουσιάσει άπειρες τέτοιες τροχιές.
Συχνά τα διαγράμματα φάσης αποκαλύπτουν ότι η πλειοψηφία των τροχιών καταλήγουν να πλησιάζουν ένα κοινό όριο. Το σύστημα τελικά εκτελεί την ίδια κίνηση για όλες τις αρχικές καταστάσεις σε μια περιοχή γύρω από την κίνηση, σχεδόν σαν να έλκεται το σύστημα σε αυτή την κίνηση. Μια τέτοια ελκυστική κίνηση καλείται ελκυστής του συστήματος.
Ένας εύκολος τρόπος να απεικονιστεί ένας χαοτικός ελκυστής είναι να αρχίσει με ένα σημείο στη ‘λεκάνη’ της έλξης του ελκυστή, και έπειτα απλά να σχεδιαστεί η επόμενη τροχιά του. Κι αυτό πιθανά μπορεί να παραγάγει μια εικόνα ολόκληρου του τελικού ελκυστή.
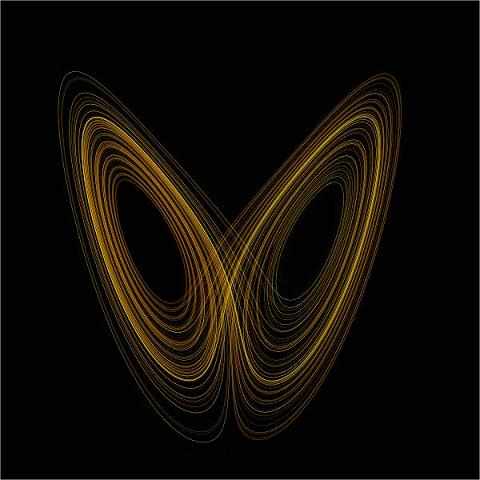Ένα διάγραμμα του παράξενου ελκυστή Lorenz για τιμές r = 28, σ = 10, b = 8/3
Παραδείγματος χάριν, σε ένα σύστημα που περιγράφει ένα εκκρεμές, το διάστημα φάσης μπορεί να είναι δισδιάστατο, που περιέχει πληροφορίες για τη θέση και την ταχύτητα. Έτσι, μπορεί να σχεδιαστεί η θέση x ενός εκκρεμούς ως προς στην ταχύτητά του u. Ένα εκκρεμές σε ηρεμία θα σχεδιαστεί ως ένα σημείο, και ένα εκκρεμές σε περιοδική κίνηση θα σχεδιαστεί ως μια απλή κλειστή καμπύλη. Όταν μια τέτοια κίνηση σχηματίζει μια κλειστή καμπύλη, η καμπύλη τότε λέγεται τροχιά. Το εκκρεμές αυτό έχει έναν άπειρο αριθμό τέτοιων τροχιών, που σχηματίζουν ένα σχέδιο ένθετων ελλείψεων.
Παράξενοι ελκυστές
Ενώ οι περισσότεροι από τους τύπους των προαναφερθέντων περιοδικών κινήσεων προκαλούν πολύ απλούς ελκυστές, όπως σημεία και καμπύλες σαν κύκλους που λέγονται κύκλοι ορίου, η χαοτική κίνηση προκαλεί αυτό που είναι γνωστό ως παράξενους ελκυστές, δηλαδή ελκυστές που μπορούν να έχουν μεγάλες λεπτομέρειες και μια πολυπλοκότητα. Παραδείγματος χάριν, ένα απλό τρισδιάστατο μοντέλο του καιρικού συστήματος του Lorenz προκαλεί το διάσημο ελκυστή του Lorenz (πάνω σχήμα). Ο ελκυστής του Lorenz είναι ίσως ένα από τα πιο γνωστά χαοτικά διαγράμματα συστημάτων, επειδή πιθανώς ήταν όχι μόνο από τα πρώτα διαγράμματα, αλλά επειδή είναι ένα από το πιο σύνθετο και σε αυτή τη μορφή είναι ένα πολύ ενδιαφέρον σχέδιο που μοιάζει με τα φτερά μιας πεταλούδας. Ένας άλλος τέτοιος ελκυστής.
Οι παράξενοι ελκυστές εμφανίζονται και στα συνεχή δυναμικά συστήματα (όπως το σύστημα του Lorenz) και σε μερικά ιδιαίτερα άλλα συστήματα. Επίσης, άλλα ιδιαίτερα δυναμικά συστήματα λέγονται σύνολο Julia, που σχηματίζονται στο όριο μεταξύ των λεκανών της έλξης των σταθερών σημείων – τα σύνολα της Julia μπορούν να θεωρηθούν ως παράξενοι απωθητές. Και οι παράξενοι ελκυστές και τα σύνολα Julia έχουν χαρακτηριστικά μια φράκταλ δομής.
Επιστροφή στον Υπερίωνα
Το πιο συνηθισμένο σχήμα για τα ουράνια σώματα είναι η σφαίρα, ή, για την ακρίβεια, το σφαιροειδές: η Γη, για παράδειγμα είναι πεπλατυσμένη στους πόλους της κατά ένα μικρό ποσοστό. Αντίθετα, ο Υπερίων, έχει σχήμα ελλειψοειδές, του οποίου οι κύριοι άξονες (μήκος, πλάτος’ ύψος) είναι 190 χλμ., 145 χλμ., και 114 χλμ. Μια “ουράνια πατάτα”.
Σύμφωνα με τις ανακαλύψεις του Κέπλερ και του Νεύτωνα, η τροχιά του Υπερίωνα γύρω από τον Κρόνο είναι ελλειπτική. Ο βαθμός κατά τον οποίο μια έλλειψη αποκλίνει από το κυκλικό σχήμα, μετριέται από μια ποσότητα γνωστή ως εκκεντρότητα: η τροχιά του Υπερίωνα έχει εκκεντρότητα γύρω στο δέκα τις εκατό. Αυτό το ποσοστό είναι ασυνήθιστα μεγάλο για τους πλανήτες και τους δορυφόρους του Ηλιακού Συστήματος, αλλά σημαίνει απλώς ότι η τροχιά είναι ένας ελαφρά πεπλατυσμένος κύκλος.
Η θέση του Υπερίωνα πάνω στην τροχιά του είναι κανονική και προβλέψιμη. Θα μπορούσαμε να την καταγράψουμε δεκαετίες πιο πριν, με χρονική ακρίβεια κλασμάτων του δευτερολέπτου. Αυτό που κάνει τον Υπερίωνα μοναδικό ανάμεσα σ’ όλους τους δορυφόρους και τους πλανήτες του Ηλίου είναι οι διακυμάνσεις του πάνω στην τροχιά: οι μεταβολές των διευθύνσεων του προς τις οποίες στρέφονται οι τρεις άξονες του. Οι περισσότεροι πλανήτες προχωρούν κυλώντας σαν μπάλες ποδοσφαίρου πάνω σε ομαλό γήπεδο.
Ο Υπερίων μοιάζει περισσότερο με μπάλα του ράγκμπυ που αναπηδά πάνω σε πεδίο μάχης. Αν μπορούσαμε να καθηλώσουμε το κέντρο του, και να παρακολουθήσουμε την κίνηση του ως προς αυτό, θα τον βλέπαμε να λικνίζεται σχεδόν τυχαία προς κάθε κατεύθυνση. Η θέση του στην τροχιά, και η στάση του καθορίζονται από τους ίδιους φυσικούς νόμους, από τις ίδιες μαθηματικές εξισώσεις. Η θέση του αντιστοιχεί σε μια κανονική λύση αυτών των εξισώσεων, η συμπεριφορά του, όμως, αντιστοιχεί σε μια μη κανονική λύση.
Οι “τούμπες του Υπερίωνα δεν οφείλονται σε τυχαίες εξωτερικές επιδράσεις, άλλα σε δυναμικό χάος. Γιατί ο Υπερίωνας είναι χαοτικός; Κι αφού αυτός είναι χαοτικός, γιατί όλα τα άλλα ουράνια σώματα είναι κανονικά; Μήπως επειδή έχει σχήμα πατάτας; Μήπως όλες οι πατάτες είναι χαοτικές;
Καθόλου. Οι αιτίες είναι πιο λεπτές, πιο σύνθετες, και πιο ενδιαφέρουσες. Η χαοτική κίνηση του Υπερίωνα οφείλεται σε μια κοσμική σύμπτωση. Στην ιστορία του Ηλιακού Συστήματος, πολλά ουράνια σώματα έχουν εισέλθει – και έχουν εξέλθει – σε κάποια περίοδο δυναμικού χάους Συμβαίνει, όμως, ο Υπερίωνας να υφίσταται αυτήν την διαδικασία ακριβώς την εποχή που το ανθρώπινο γένος άρχισε να ενδιαφέρεται γι’ αυτήν.
Νομίζουμε ότι είμαστε σε θέση να καταλάβουμε πώς βρέθηκε ο Υπερίων στην τωρινή χαοτική κατάσταση του.
Στο μακρινό παρελθόν, η περίοδος περιστροφής του Υπερίωνα γύρω απ’ τον εαυτό του (“η ημέρα”) ήταν συντομότερη σε σχέση με την περίοδο της τροχιάς του (“το έτος”). Η κίνηση του ήταν τότε κανονική και ημιπεριοδική. Με την πάροδο των αιώνων, οι παλιρροϊκές δυνάμεις του Κρόνου μείωσαν την ταχύτητα των περιστροφών του και ανόρθωσαν τελικά τον Υπερίωνα, έτσι ώστε ο άξονας περιστροφής του να γίνει ο μεγαλύτερος αδρανειακός άξονας και να τεθεί κάθετος προς το επίπεδο της τροχιάς. Ωστόσο από τότε που ο Υπερίων έχασε ενέργεια αρκετή ώστε να εισαχθεί στη χαοτική περιοχή, το αποτέλεσμα εκατομμυρίων ετών ανατράπηκε μέσα σε λίγες μόνο μέρες. Μέσα σε τρεις ή τέσσερις τροχιακές περιστροφές, ο Υπερίων άρχισε να κατρακυλά προς όλες τις κατευθύνσεις.
Θα πρέπει να αναφέρουμε ότι αυτή η πρόβλεψη του χαοτικού κατρακυλίσματος του Υπερίωνα δεν έχει ακόμη απόλυτα εδραιωθεί από άμεσες παρατηρήσεις. Όμως, οι φωτογραφίες του Voyager συμφωνούν με το χαοτικό κατρακύλισμα, ενώ δεν συμφωνούν με καμιά γνωστή κανονική κατάσταση. Η θεωρία μοιάζει με πολύ σίγουρο στοίχημα. Ίσως κατορθώσουμε να την ελέγξουμε για μια μεγαλύτερη χρονική περίοδο αναλύοντας την ένταση του φωτός που επιστρέφει στη Γη μετά από ανάκλαση πάνω στον Υπερίωνα: θα πρέπει κι αυτό να μεταβάλλεται επίσης ακανόνιστα.
Ο Υπερίων είναι ο μόνος δορυφόρος του Ηλιακού Συστήματος, ο οποίος συνεχίζει, ίσως, να κατρακυλά μ’ αυτόν τον τρόπο. Η ίδια ανάλυση, όμως, οδηγεί στο συμπέρασμα ότι όλοι οι ακανόνιστα σχηματισμένοι δορυφόροι θα πρέπει — σε κάποιο στάδιο της εξέλιξης τους — να περάσουν από μια περίοδο χαοτικού κατρακυλίσματος. Οι Δείμος και Φόβος, οι δύο δορυφόροι του Άρη, θα πρέπει να κατρακυλούσαν χαοτικά στο μακρινό παρελθόν. Το ίδιο και ο μικρότερος δορυφόρος του Ποσειδώνα, η Νηρηίς.
Οι τελευταίες παρατηρήσεις μας δείχνουν ότι η διεύθυνση του άξονα περιστροφής του και η γωνιακή του ταχύτητα εκτελούν μια χαοτική κίνηση. Θεωρητική μελέτη της κίνησης αυτής δείχνει ότι η εκδήλωση της χαοτικής κίνησης είναι συνέπεια του γεγονότος ότι ο Υπερίων προσπαθεί να ταλαντωθεί μεταξύ δύο συντονισμών (πρόκειται για τους συντονισμούς 3/2 και 1/1 μεταξύ περιστροφής περί τον άξονά του και περιφοράς περί τον Κρόνο) και η επικάλυψη αυτή των συντονισμών είναι ένας από τους μηχανισμούς δημιουργίας χάους. Η περίπτωση του Υπερίωνα είναι η μόνη, μέχρι στιγμής, περίπτωση όπου έχουμε άμεση παρατήρηση χαοτικής κίνησης στο Ηλιακό σύστημα.
Κβαντική Χαολογία
Το χάος αποκαλύφθηκε από τη Μαθηματική φαντασία, και γεννήθηκε από τη Φυσική. Αλλά πού, άραγε, πηγαίνει; Πηγαίνει μέσα σε κάθε φυσικό φαινόμενο που παρουσιάζει αταξία, αλλά με συνθήκες που υποδηλώνουν ότι υπάρχει μια υποκείμενη δομή. Τέτοια φαινόμενα εμφανίζονται παντού.
Μια ενδιαφέρουσα κατεύθυνση, την οποία — παρά την μικρή αναφορά στον Αϊνστάιν — αγνοήσαμε μέχρι τώρα, είναι η κβαντομηχανική. Την παραβλέψαμε επειδή δεν έχουμε σοβαρή αιτιολογία για να πιστεύουμε ότι η χαοτική δυναμική, όπως την ξέρουμε σήμερα παρέχει κάποια λύση στο ερώτημα του Αϊνστάιν. Όμως, το χάος σχετίζεται με την κβαντομηχανική, γι αυτό και θα το αναλύσουμε περισσότερο.
Ο όρος Χαολογία πολύ παλιά αναφερόταν στη μελέτη της εποχής του χάους — την περίοδο όπου “η Γη ήταν άδεια και χωρίς σχήμα”. Η χαολογία δεν είναι πια ένας ενεργός τομέας της θεολογίας, κι έτσι ο όρος είναι ελεύθερος για μια πιο σύγχρονη σημασία: τη μελέτη του ντετερμινιστικού χάους.
Η κβαντομηχανική είναι η σύγχρονη φυσική για το σύμπαν σε ατομικές κλίμακες μέτρησης. Στην κβαντομηχανική, ποσότητες όπως η ενέργεια δεν είναι συνεχείς: αντίθετα, εμφανίζονται σε διακριτά κομμάτια, τα κβάντα. Το μέγεθος ενός μόνου κβάντου είναι αφάνταστα μικρό, και δίνεται από έναν πολύ μικρό αριθμό, γνωστό σαν σταθερά του Πλανκ (Plank). Και τα σωματίδια δεν είναι καθόλου σωματίδια, αλλά μια δυαδικότητα σωματιδίου – κύματος, που περιγράφεται από μια κυματοσυνάρτηση της κβαντομηχανικής.
Σε μια δημοφιλή ερμηνεία, η κυματοσυνάρτηση δεν αντιπροσωπεύει την κατάσταση ενός σωματιδίου, αλλά μια υπέρθεση όλων των δυνατών καταστάσεων, και όταν πραγματοποιείται μια παρατήρηση, η κυματομορφή “συμπιέζεται” σε μια μόνη κατάσταση. Πριν από αυτόν τον εκφυλισμό, το τετράγωνο της κυματοσυνάρτησης αντιπροσωπεύει την πιθανότητα με την οποία το σύστημα θα βρεθεί σε μια δεδομένη κατάσταση.
Αυτή ή άποψη δεν άρεσε στον Αϊνστάιν. Γι αυτό και έγραψε στον Μαξ Μπόρν:
Εσύ πιστεύεις σ’ ένα Θεό που παίζει ζάρια, κι εγώ πιστεύω στην αυστηρή νομοτέλεια και την τάξη, σ’ ένα κόσμο που υπάρχει αντικειμενικά, και τον οποίο, μ’ έναν παράλογα στοχαστικό τρόπο, προσπαθώ να συλλάβω. Το πιστεύω ακράδαντα, αλλά ελπίζω ότι κάποιος θα ανακαλύψει έναν πιο ρεαλιστικό τρόπο, ή μάλλον θα θέσει μια πιο χειροπιαστή βάση από αυτή που μου έλαχε να θέσω εγώ. Ακόμη κι η σπουδαία αρχική επιτυχία της κβαντικής θεωρίας δεν με πείθει στο θεμελιώδες παιχνίδι των ζαριών, αν και ξέρω καλά ότι οι νεαροί συνεργάτες σου ερμηνεύουν αυτή μου την άποψη σαν επακόλουθο των γηρατειών.
Παρ’ όλ’ αυτά, τα κβαντομηχανικά γεγονότα φαίνονται ακόμη να πραγματοποιούνται με τον τρόπο που προσδιορίζει η κβαντομηχανική. Και ενώ η στατιστική της ραδιενεργούς διάσπασης, για παράδειγμα, ακολουθεί συγκεκριμένους νόμους, κανείς δεν μπορεί να προβλέψει πότε ένα δεδομένο άτομο θα φτάσει στο κρίσιμο σημείο να αποσυντεθεί. Ο Θεός παίζει ζάρια, ή παίζει ένα βαθύτερο παιχνίδι που δεν έχουμε ακόμη κατανοήσει;
Ο Αϊνστάιν συμφωνούσε με την δεύτερη ιδέα — το βαθύτερο παιχνίδι που ακόμα δεν το καταλαβαίνουμε.
Λοιπόν, έχουμε συνειδητοποιήσει οριστικά ότι το ντετερμινιστικό χάος ευθύνεται για ένα μεγάλο μέρος της παρατηρημένης τυχαιότητας στην κλασική μηχανική. Μήπως το κβαντικό χάος είναι υπεύθυνο για την παρατηρημένη τυχαιότητα και στην κβαντομηχανική; Μήπως μπορούμε τώρα να εμβαθύνουμε στο βαθύτερο παιχνίδι του Θεού;
Όχι, δεν μπορούμε προς το παρόν. Αν όντως υπάρχει κάποιο βαθύτερο παιχνίδι, είναι ακόμα πολύ βαθύ για μας, τα μαθητευόμενα μικρά πλασματάκια. Χρειαζόμαστε απεγνωσμένα έναν Αληθινό Άνθρωπο για να μας βάλει στο σωστό δρόμο.
Χάος στο ηλιακό σύστημα
Πολλοί κομήτες κατά καιρούς εισέρχονται στο ηλιακό μας σύστημα και πλησιάζουν την τροχιά της Γης. Η δεξαμενή των κομητών αυτών είναι έξω από τα όρια του ηλιακού συστήματος, πιο πέρα από την τροχιά του Ποσειδώνα, σε μια ζώνη που εκτείνεται από 35 μέχρι και 500 ακτίνες της γήινης τροχιάς. Η ζώνη αυτή είναι παρόμοια με τη ζώνη των αστεροειδών και ονομάζεται ζώνη του Kuiper. Έχει βρεθεί ότι σε πολλά σώματα εκεί μέσα που η τροχιά τους αρχικά ήταν περίπου κυκλική, να γίνεται σε μικρό χρονικό διάστημα πολύ επιμήκης (ελλειπτική με μεγάλη εκκεντρότητα) και συνεπώς να επισκέπτονται το εσωτερικό ηλιακό σύστημα ως κομήτης. Οι τροχιές όλων αυτών των κομητών είναι χαοτικές, διότι έφθασαν σε εμάς μέσω χαοτικής διαδικασίας. Αυτοί είναι οι κομήτες μικρής περιόδου (μέχρι 200 έτη). Ένας τέτοιος κομήτης είναι και ο κομήτης του Halley, του οποίου η τροχιά είναι χαοτική και συνεπώς μη προβλέψιμη. Πράγματι, αριθμητικοί υπολογισμοί έχουν δείξει ότι δεν μπορούμε να προβλέψουμε την ακριβή θέση του κομήτη του Halley για χρονικό διάστημα μεγαλύτερο από 29 περιφορές του γύρω από τον Ήλιο.
Υπάρχουν και κομήτες πολύ μεγαλύτερης περιόδου (από 1 μέχρι 30 εκατομμύρια έτη) που προέρχονται από μια πολύ πιο μακρινή “δεξαμενή”, το νέφος του Oort, που έχει σφαιρική κατανομή γύρω από το Ηλιακό σύστημα. Η τροχιές των κομητών μακράς περιόδου είναι επίσης χαοτικές.
Έχει αποδειχθεί ότι η ύπαρξη της Σελήνης παίζει σταθεροποιητικό ρόλο στην κίνηση του άξονα περιστροφής της Γης. Βρέθηκε ότι υπάρχει μια ευρεία χαοτική περιοχή, όσον αφορά την κίνηση του άξονα περιστροφής της Γης, που οφείλεται σε επικάλυψη συντονισμών. Ο άξονας της Γης αποφεύγει αυτή τη χαοτική περιοχή λόγω υπάρξεως της Σελήνης, η οποία μέσω της βαρυτικής επιδράσεώς της στη Γη κρατάει τη θέση του άξονα περιστροφής έξω από τη χαοτική περιοχή. Έτσι η θέση του άξονα της Γης εκτελεί οργανωμένη κίνηση, με συνέπεια τη σταθερότητα του κλίματος. Είναι γνωστό ότι το κλίμα επηρεάζεται από την κλίση του άξονα περιστροφής και απρόβλεπτες, χαοτικές, κινήσεις θα είχαν ως συνέπεια τη μη σταθερότητα του κλίματος και ίσως τη μη ανάπτυξη της ζωής. Αν η Σελήνη είχε μικρότερη μάζα, ή αν δεν υπήρχε καθόλου, δεν θα μπορούσε να παίξει το σταθεροποιητικό της ρόλο και η διεύθυνση του άξονα περιστροφής της Γης θα εκτελούσε χαοτική κίνηση.
Τέλος, οι προηγούμενες περιπτώσεις αναφέρονταν σε επιμέρους περιοχές του ηλιακού συστήματος, όπου είχαμε την εμφάνιση χαοτικών κινήσεων. Αλλά υπολογισμοί για την εξέλιξη ολόκληρου του Ηλιακού συστήματος έδειξαν ότι το Ηλιακό σύστημα και ειδικότερα το εσωτερικό Ηλιακό σύστημα (οι μικροί πλανήτες Ερμής, Αφροδίτη, Γη, Άρης) παρουσιάζουν χαοτική συμπεριφορά. Η χαοτική συμπεριφορά εμφανίζεται όμως μετά από πολύ μεγάλα (για την καθημερινή ζωή) χρονικά διαστήματα και έχει ως αποτέλεσμα την απρόβλεπτη εξέλιξη κυρίως του προσανατολισμού της τροχιάς της Γης και των άλλων μικρών πλανητών και λιγότερο της εκκεντρότητας και της κλίσεως της τροχιάς τους. Αυτό σημαίνει ότι δεν είναι δυνατή η πρόβλεψη της θέσης ενός μικρού πλανήτη μετά από κάποιο χρονικό διάστημα. Το χρονικό αυτό διάστημα όμως είναι της τάξεως των 100 εκατομμυρίων ετών.
Συμπέρασμα: Βλέπουμε ότι η φύση είναι μη γραμμική, δηλαδή οι νόμοι που καθορίζουν την εξέλιξη ενός φαινομένου δεν είναι αναλογικοί στη σχέση μεταξύ αιτίας και αποτελέσματος. Σήμερα γνωρίζουμε ότι τέτοια μη γραμμικά συστήματα εμφανίζουν χάος και συνεπώς και όλη η φύση είναι χαοτική. Κατά συνέπεια, δεν είναι δυνατό να γίνουν προβλέψεις για την κίνηση των πλανητών και των λοιπών σωμάτων στο Ηλιακό σύστημα, όπως άλλωστε και σε κάθε άλλο φυσικό σύστημα. Το χρονικό όμως διάστημα που απαιτείται για να γίνει αισθητή η παρουσία του χάους στο Ηλιακό σύστημα είναι μεγάλο, με τα μέτρα της καθημερινής ζωής.
Όπως όμως κάθε μεγάλο άλμα της επιστήμης, έτσι και η θεωρία του χάους έβαλε και νέους περιορισμούς στις ανθρώπινες δυνατότητες. Η θεωρία της σχετικότητας του Einstein επέβαλε τον σοβαρό περιορισμό ότι δεν μπορούμε να υπερβούμε την ταχύτητα του φωτός. Η θεωρία του χάους, που θεωρείται ένα νέο άλμα της επιστήμης, έκανε απαγορευτική την πρόβλεψη ενός φαινομένου για μεγάλα χρονικά διαστήματα. Ειδικότερα, στο ηλιακό σύστημα δεν μπορούμε να προβλέψουμε ποιά θα είναι η θέση των πλανητών μετά από εκατό εκατομμύρια χρόνια. Το διάστημα αυτό μπορεί να φαίνεται πολύ μεγάλο για την καθημερινή ζωή, σε αστρονομική κλίμακα όμως είναι μικρό. Πράγματι, σε σχέση με την ηλικία του Ηλιακού συστήματος (4.6 δισεκατομμύρια χρόνια), είναι περίπου τα δύο εκατοστά της ηλικίας του.
* Το άρθρο αυτό βασίστηκε στο βιβλίο Παίζει ο Θεός ζάρια του Ian Stewart, στο άρθρο ΧΑΟΣ ΣΤΟ ΗΛΙΑΚΟ ΣΥΣΤΗΜΑ του καθηγητή Ι. Χατζηδημητρίου, και σε παλαιότερα άρθρα του physics4u
Δείτε και τα σχετικά άρθρα
1. Το Χάος ελευθερώνει το Σύμπαν
Leave a Comment