O Κλοντ Σάνον (Claude Shannon) γεννήθηκε 30 Απριλίου του 1916. Ήταν Αμερικανός μαθηματικός, στοχαστής, ηλεκτρολόγος μηχανικός, και κρυπτογράφος, γνωστός ως «ο πατέρας της θεωρίας πληροφορίας». Ο άνθρωπος που κατά τη δεκαετία του ’40, θεμελίωσε την θεωρία της πληροφορίας και ανέδειξε την πληροφορία σε μετρήσιμο μέγεθος. Έθεσε έτσι τα θεμέλια για τα τηλεπικοινωνιακά δίκτυα και με αυτόν τον τρόπο βοήθησε να αναπτυχθεί η σημερινή Κοινωνία της Πληροφορίας. Είναι μεγάλη ειρωνεία το γεγονός ότι ένα τόσο κοφτερό, γόνιμο και πολυδουλεμένο μυαλό τα τελευταία χρόνια προσβλήθηκε από τη νόσο του AΙzheimer και πέθανε στην ηλικία των 85 ετών. 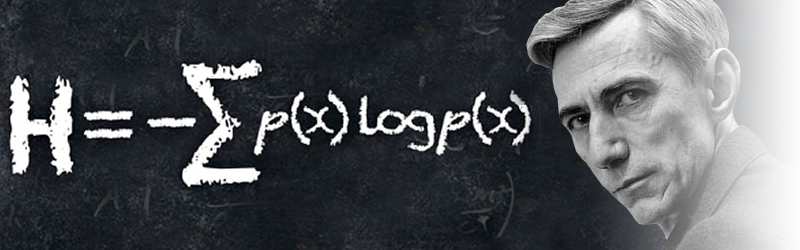
Αποφοίτησε το 1936, από το Πανεπιστήμιο του Michigan, παίρνοντας δύο πτυχία του Μαθηματικού και του Ηλεκτρολόγου Μηχανικού. Τις μεταπτυχιακές του σπουδές τις έκανε στο ΜΙΤ, όπου είχε σαν καθηγητή και τον Norbert Wiener (που ήταν ο πρώτος που χρησιμοποίησε τη λέξη Κυβερνητική).
Ο πρύτανης του τμήματος Μηχανολογίας την εποχή εκείνη, όρισε τον Shannοn υπεύθυνο για τη λειτουργία μιας δύσχρηστης υπολογιστικής συσκευής, που είχε κατασκευάσει ο ίδιος και είχε ονομάσει “διαφορικό αναλυτή”. Εκείνος δε άρχισε να σκέφτεται τρόπους βελτίωσής του, ενδεχομένως με τη χρήση ηλεκτρικών κυκλωμάτων στη θέση των δύσχρηστων μηχανικών μερών.
Ο CΙaυde Shannοn δεν άργησε να σκεφθεί ότι η άλγεβρα του Boole που είχε διδαχθεί ως προπτυxιακός φοιτητής είχε πολλά κοινά στοιχεία με ένα ηλεκτρικό κύκλωμα. Το επόμενο λογικό βήμα ήταν να σχεδιάσει συστήματα κυκλωμάτων, σύμφωνα με τις αρχές που είχε διατυπώσει ο Βοοle στα μέσα του 18ου αιώνα.
Σε μια διατριβή του, με τίτλο “Α SymbοΙic Analysis οf Relay and Switching Circυίts”, ο Shannοn περιέγραψε με ποιο τρόπο η λογική του Bοοle, σύμφωνα με την οποία όλα τα προβλήματα μπορούν να λυθούν με τη χρήση μόλις δύο συμβόλων, του 1 και του 0, μπορούσε να εφαρμοστεί στα ηλεκτρικά διακοπτόμενα κυκλώματα.
Το σύμβολο 1 μπορούσε να αντιπροσωπεύει ένας διακόπτης που είχε ενεργοποιηθεί, ενώ το 0 μπορούσε να είναι ένας διακόπτης που είχε απενεργοποιηθεί.
Υποστήριξε επίσης ότι οι διακόπτες αυτοί θα μπορούσαν να συνδέονται με τρόπο που να τους επιτρέπει να εκτελούν και πιο πολύπλοκες πράξεις, προτείνοντας πέρα από τις απλές δηλώσεις “ναι” και “όχι”, τη χρήση του “και” , του “ή” ή του “δεν”.
Η παραπάνω διατριβή του Shannοn, ο οποίος οραματίστηκε όλες τις μορφές επικοινωνίας σε δυαδικό κώδικα και υποστήριξε την άποψη ότι τα δυαδικά ψηφία μπορούν να συμβολίσουν ακόμα και λέξεις, ήχους, εικόνες, ίσως και ιδέες, χαρακτηρίστηκε μία από τις σημαντικότερες του 20ού αιώνα, ξεπερνώντας σε αξία ακόμα και τη προηγούμενη διατριβή του ίδιου για το διδακτορικό του, με θέμα “Μια άλγεβρα για τη θεωρητική γενετική”. Σε αυτήν την διατριβή θεωρούσε πως η διπλή έλικα του DNA σποτελεί ένα πληροφοριακό σύστημα.
Το 1941 προσλήφθηκε στην BeΙΙ ΤeΙeρhοne Labοratοries, όπου αρχικά ασχολήθηκε με συστήματα ελέγχου αντιαεροπορικών πυραύλων και στη συνέχεια έγινε μέλος μιας ομάδας επιστημόνων που ανέλαβε να αναπτύξει πιο αποτελεσματικές μεθόδους μετάδοσης των πληροφοριών και να βελτιώσει την αξιοπιστία των υπεραστικών τηλεφωνικών και τηλεγραφικών γραμμών.
Ο Shannοn πίστευε ότι η πληροφορία δεν διέφερε από οποιοδήποτε άλλο μέγεθος και κατά συνέπεια ήταν δυνατός ο χειρισμός της από μηχανές. Εφαρμόζοντας τα αποτελέσματα των προηγούμενων ερευνών του στο πρόβλημα που είχε να αντιμετωπίσει, χρησιμοποίησε και πάλι τη λογική του ΒοοΙe, καθώς και την εμπειρία του στην κρυπτο / αποκρυπτογράφηση κατά τη διάρκεια του πολέμου, για να αναπτύξει ένα μοντέλο που απλοποιούσε όσο το δυνατόν περισσότερο την πληροφορία.
Ενα δυαδικό σύστημα από δυνατότητες επιλογής ναι/όχι που μπορούσε να αντιπροσωπεύεται από δυαδικό κώδικα 1/0. Πρότεινε επίσης την προσθήκη στην πληροφορία μιας σειράς από ειδικούς κώδικες κατά τη διάρκεια της μετάδοσής της, με στόχο να ελαχιστοποιούνται τα παράσιτα (θόρυβος) που έχουν ως αποτέλεσμα την αλλοίωσή της.
Η ΘΕΩΡΙΑ ΤΗΣ ΠΛΗΡΟΦΟΡΙΑΣ
Πρώτος ο Hartley όρισε έμμεσα την ποσότητα της πληροφορίας, το 1928. Ένα χρόνο αργότερα ο Szilard συνέδεσε την πληροφορία και την Θερμοδυναμική Εντροπία.
Το 1940 ο Shannon ξαναβρήκε τα ίδια αποτελέσματα με αφορμή τις τηλεποικινωνίες. Η καθαυτό όμως θεωρία της πληροφορίας αναπτύχθηκε από τους Wiener (“Θεωρία για την διεύθυνση και επικοινωνία, στη μηχανή ή στο ζώο”) το 1948 και ακολούθως από τον Shannon.
Το 1948 ο Shannοn δημοσίευσε την αξεπέραστη εργασία του, με τίτλο “Η μαθηματική θεωρία της πληροφορίας”. Ήταν ο πρώτος που έκανε την πρώτη ολοκληρωτική μαθηματική απόπειρα θεμελίωσης της Θεωρίας της Πληροφορίας. Στις σελίδες αυτής της εργασίας, την οποία συνυπογράφει ο μαθηματικός Warren Weaνer, γίνεται λόγος για πρώτη φορά για μια μονάδα μέτρησης της πληροφορίας, το δυαδικό ψηφίο, το binary digit, που συντμήθηκε αργότερα από επιστήμονες του χώρου αρχικά σε binit και στη συνέχεια στο γνωστό μας bit.
Έχουμε συνηθίσει να σκεφτόμαστε την “πληροφορία” ή το “μήνυμα” ως γεγονότα, δεδομένα, μαρτυρίες. Σύμφωνα όμως με τη θεωρία της πληροφορίας, πληροφορία είναι αυτό που δεν γνωρίζει κάποιος. Αν κάποιος ακούσει πως “Αύριο θα βρέχει στο κέντρο της Αθήνας”, το μήνυμα αυτό, έχει μεγάλη πληροφορία, γιατί είναι ένα αβέβαιο γεγονός.
Αν όμως ακούσει κάποιος πως “στην Ευρώπη αύριο θα βρέχει”, τότε το κείμενο αυτό έχει πολύ μικρή πληροφορία. Γιατί στο μήνυμα αυτό η πιθανότητα να βρέχει κάπου στην Ευρώπη είναι πολύ μεγάλη, ίσως αγγίζει και το 100%.
Επομένως η πληροφορία συνδέεται με την αβεβαιότητα. Όσο μικρότερη είναι η πιθανότητα Ρ να γίνει ένα γεγονός, τόση περισσότερη ποσότητα πληροφορίας Ι συνοδεύει την πραγματοποίηση του. Και αντίστροφα, αν η πιθανότητα Ρ πραγματοποίησης ενός γεγονότος είναι μεγάλη, τότε η πληροφορία Ι που “κουβαλάει” το γεγονός αυτό είναι μικρή. Αν λοιπόν ο παραλήπτης έχει ήδη την πληροφορία, δεν μπορεί να πει κανείς ότι έλαβε χώρα μετάδοση μηνύματος.
Η πληροφορία Ι συνδέεται με την πιθανότητα Ρ με την σχέση:
Ι=-log2PA ή Ι=log2(1/p).
Η μορφή αυτή μας δίνει την γνωστή μονάδα ποσότητας πληροφορίας, το bit. Αν έχουμε μια απλή πηγή που εκπέμπει δύο σύμβολα μόνο, τότε αν και τα δύο είναι ισοπιθανά ισχύει ,
pa=pb=1/2, και Ι=1 ή Ι=1 bit.
Σύμφωνα με τη θεωρία του Shannοn, περισσότερα bits πληροφορίας παίρνει κανείς από ένα μήνυμα, αν είναι μεγαλύτερη και η αβεβαιότητα που κουβαλάει το μήνυμα, γιατί αυτή η αβεβαιότητα είναι αντιστρόφως ανάλογη με την πιθανότητα Ρ να συμβεί όπως αναφέραμε πιό πάνω.
ΕΝΤΡΟΠΙΑ
Ένα από τα σημαντικότερα στοιχεία όμως του έργου του Shannοn είναι ότι παρέχει στους μηχανικούς τα μαθηματικά εργαλεία που απαιτούνται για τη μέτρηση της απόδοσης ενός καναλιού επικοινωνίας, πόση πληροφορία δηλαδή μπορεί να ξεκινήσει από το σημείο Α και να φθάσει στο σημείο Β χωρίς σφάλματα. Η επιθυμητή πληροφορία είναι το “σήμα”. Η ανεπιθύμητη είναι τα “παράσιτα” ή ο “θόρυβος”.
Ο Shannon είδε πως όσο λιγότερο θόρυβο έχει ένα σύστημα τόση περισσότερη πληροφορία μεταδίδει. Και αντιστρόφως, όσο αυξάνεται η αταξία (θόρυβος) ενός συστήματος τόσο λιγότερη πληροφορία μεταδίδει. Θα μπορούσαμε να πούμε πως η πληροφορία του συστήματος αποτελεί μέτρο της εσωτερικής του τάξης (δηλ. αντιστρόφως ανάλογη με την αταξία, αλλά η εντροπία είναι το μέτρο της αταξίας ενός συστήματος, άρα η πληροφορία είναι αντιστρόφως ανάλογη της εντροπίας).
Ο αριθμός των πιθανών μηνυμάτων που μπορεί κανείς να δημιουργήσει με S αριθμό bits είναι 2 στη δύναμη του S, δεδομένου ότι έχουμε δύο bits, το 1 και το 0.
Αντιστρέφοντας την ιδέα, ο αριθμός των bits που χρειάζεται κανείς για να μεταδώσει ένα μήνυμα είναι ο λογάριθμος με βάση το 2 του αριθμού των πιθανών μηνυμάτων.
2S=P ή λογαριθμίζοντας Ιοg2 P = S
Στην αξία του S ο Shannοn έδωσε το όνομα “εντροπία”. Η εντροπία αναφέρεται σε μια κατάσταση ενός φυσικού συστήματος, ενώ συγχρόνως αποτελεί μέτρο της αταξίας του συγκεκριμένου συστήματος. Η αταξία δεν είναι τελείως αντικειμενική ιδιότητα. Ο ανθρώπινος παράγοντας δεν μπορεί να την αποκλείσει τελείως, γιατί η ιδέα της τάξης είναι άρρηκτα συνδεδεμένη με τη λειτουργία του νου.
Το εντυπωσιακό με την εξίσωση του Shannοn για την εντροπία της πληροφορίας είναι ότι εμφανίζει την ίδια σχέση με την εξίσωση του BοΙtzmann (S=klnP) για την εντροπία στη θερμοδυναμική (δεύτερος νόμος), μια σχέση λογαριθμική.
Από τον ορισμό του Boltzmann και του Shannon για την πιθανότητα,
S=klnP και Ι=-log2PA,
είναι έκδηλη η ομοιότητα των σχέσεων ορισμού της πληροφορίας και της εντροπίας. Βλέπουμε δηλαδή πως ενώ η εντροπία μετράει το βαθμό αταξίας και αυξάνει με την πιθανότητα, η πληροφορία ουσιαστικά μετράει το βαθμό της τάξης μέσα στη δομή του μηνύματος και ελαττώνεται με την πιθανότητα.
Αυτός είναι βασικά και ο λόγος που βάζουμε Ι=-S και που συχνά αναφέρουμε την πληροφορία Ι σαν αρνητική εντροπία S (αντετροπία-negentropie).
Ο Shannοn δεν προσπάθησε να εξαλείψει την αταξία, τα παράσιτα. Μας δίδαξε πώς να ζούμε με αυτά ή ακόμα και να τα αξιοποιούμε. Μπορεί κανείς να χρησιμοποιήσει την εντροπία για να διαπιστώσει τι μέρος του καναλιού μπορεί να χρησιμοποιηθεί για τη μετάδοση χρήσιμης πληροφορίας – του σήματος.
Η εντροπία της θερμοδυναμικής συνεπάγεται τη φθορά. Αν θεωρήσουμε δεδομένο ότι το σύμπαν είναι ένα κλειστό σύστημα, κάθε φορά που συμβαίνει κάτι, ολόκληρο το σύστημα ολισθαίνει προς την αύξηση της εντροπίας. Η ίδια η ζωή όμως στη Γη συνεισφέρει στην μείωση της εντροπίας, ενώ στο σύμπαν η εντροπία αυξάνεται. Στη θεωρία της πληροφορίας, όσο μικρότερη είναι η εντροπία τόσο περισσότερη είναι και η πληροφορία… άρα και η αβεβαιότητα.
Αυτό σημαίνει μήπως, αναρωτιούνται κάποιοι, ότι όσο περισσότερα γνωρίζουμε τόσο περισσότερο αβέβαιοι είμαστε;
Το γεγονός ότι η πληροφορία ολοένα αυξάνει σημαίνει ότι απομακρυνόμαστε ολοένα και περισσότερο από τη δυνατότητα να κατανοήσουμε το σύμπαν;
Πέντε χρόνια μετά την έκδοση της θεωρίας της πληροφορίας του Shannοn, οι James Watsοn και Francis Crick αποκάλυψαν τα μυστικά του DNA στο εργαστήριο Caνendish του Cambridge. Διαπιστώθηκε ότι η διπλή έλικα του DNA αποτελούσε ένα πληροφοριακό σύστημα Ο ίδιος ο Shannοn, παρ’ όλο που προειδοποιούσε με δημοσιεύματα τους εργαζόμενους σε άλλα πεδία να είναι επιφυλακτικοί και να μην εφαρμόζουντη θεωρία των πληροφοριών αδιακρίτως, παραδέχθηκε ότι η θεωρία θα μπορούσε να έχει μεγάλη σχέση με τον τρόπο με τον οποίο λειτουργούν τα γονίδια και το νευρικό σύστημα και άφησε ανοιχτό το ενδεχόμενο ‘το ανθρώπινο ον να δρα ως ένας ιδανικός αποκωδικοποιητής”.
Ο Monod μας λέει πως τα ένζυμα ασκούν σε μικροσκοπική κλίμακα, μια λειτουργία που δημιουργεί τάξη, δημιουργεί πληροφορία σε βάρος του χημικού δυναμικού.
Ο Shannon διετύπωσε μια διάσημη σχέση για την χωρητικότητα C ενός καναλιού, στον οποίο φαίνεται καθαρά η σχέση μεταξύ εύρους ζώνης συχνοτήτων Β και λόγου σήματος προς θόρυβο.
C=Blog(1+S/N) bits/sec
Γεγονός είναι ότι η θεωρία της πληροφορίας που διατύπωσε ο CΙaude Shannοn ξεκίνησε την ψηφιακή επανάσταση που οδήγησε στην ανάmυξη και την εδραίωση νέων μέσων επικοινωνίας – μεταξύ των οποίων και το Ιnternet. Χρησιμοποιήθηκε επίσης για να λυθούν γρίφοι σε γνωστικούς τομείς τόσο διαφορετικούς μεταξύ τους όσο η πληροφορική, η γενετική μηχανική, τα νευρωνικά συστήματα, η γλωσσολογία, η φωνητική, η ψυχολογία και τα οικονομικά Μεταξύ άλλων άνοιξε νέους δρόμους στη μελέτη του Χάους και έφερε το Διάστημα πιο κοντά στον άνθρωπο.
Από τη στιγμή ωστόσο που διατύπωσε τα θεωρήματά του, η Φύση δεν μπορεί πια να ιδωθεί μόνο σαν ύλη και ενέργεια. Μία τρίτη συνιστώσα προστέθηκε στην προσπάθεια εξήγησης του κόσμου: η πληροφορία.
Δείτε και το άρθρο : Η θεωρίας της Πληροφορίας και της Κυβερνητικής
Βιβλιογραφία:
1. Θεωρία της Πληροφορίας και Φυσικές Επιστήμες: Κ.Καρούμπαλος
2. Περιοδικό Computer για Ολους. Τεύχος Απριλίου 2001
3. Κυβερνητική και Διαλεκτικός Υλισμός: Jacques Guillaumaud
4.Κυβερνητική:Norbert Wiener



