Πριν 100 χρόνια διατυπωνόταν στην τελική της μορφή, η Γενική Θεωρία της Σχετικότητας, από τον Αλβέρτο Αϊνστάιν, σαν γενίκευση της Ειδικής θεωρίας της Σχετικότητας. Ο Αϊνστάιν οδηγήθηκε σε αυτήν, για να μπορέσει να συμβιβάσει τα πειραματικά δεδομένα με το παλαιό νόμο της παγκόσμιας έλξης. Η νέα θεωρία θεωρείται σαν μια θεωρία της βαρύτητας, γιατί η μάζα σε αυτήν, όχι μόνο επιδρά στα υλικά σώματα αλλά αλλάζει και την έννοια του χωρόχρονου.
Περιεχόμενα Σελίδας:
Η ρήξη με την κλασσική φυσική

![]() Με την Ειδική Θεωρία της Σχετικότητας, ο Αϊνστάιν άρχισε την ρήξη με την κλασική φυσική με τέτοιες επαναστατικές ιδέες, που δεν συμφωνούσαν με τις κοινά αποδεκτές αντιλήψεις για το χρόνο και το χώρο.
Με την Ειδική Θεωρία της Σχετικότητας, ο Αϊνστάιν άρχισε την ρήξη με την κλασική φυσική με τέτοιες επαναστατικές ιδέες, που δεν συμφωνούσαν με τις κοινά αποδεκτές αντιλήψεις για το χρόνο και το χώρο.
Βρήκε λοιπόν γιατί η ταχύτητα του φωτός φαίνεται ίδια για όλους τους μη επιταχυνόμενους παρατηρητές, σύμφωνα με το πείραμα του Michelson-Morley και τις εξισώσεις του Maxwell. Περιέγραψε τι συμβαίνει όταν τα αντικείμενα κινούνται με ταχύτητες που πλησιάζουν την ταχύτητα του φωτός. Και συγχρόνως ότι δεν υπάρχει ταχύτητα μεγαλύτερη από του φωτός.
Τροποποίησε την ιδέα που είχαμε για τη μάζα, που μέχρι τότε την θεωρούσαμε σαν ένα σύμφυτο και σταθερό χαρακτηριστικό της ύλης. Για μικρές ταχύτητες η μεταβολή της μάζας είναι ανάλογη με τη μεταβολή της κινητικής ενέργειας. Έτσι οδηγούμαστε στη νέα ιδέα για την άμεση σχέση της μάζας m με την ενέργεια.
Τέλος ανήγαγε την αρχή της Σχετικότητας του Γαλιλαίου σε υπέρτατη αρχή της φυσικής, πως κάθε φυσικός νόμος είναι ο ίδιος για κάθε μη επιταχυνόμενο παρατηρητή. Δεν υπάρχει ‘αιθέρας’, δεν υπάρχει ‘απόλυτη’ κίνηση, ‘απόλυτο’ σύστημα αναφοράς διακήρυξε ο Αϊνστάιν, μόνο ‘σχετικές’ κινήσεις ‘ειδικών’ παρατηρητών. Γι’ αυτό και ονομάστηκε η πρώτη θεωρία του, Ειδική Θεωρία της Σχετικότητας. Με τη λέξη ‘ειδική’ εννούσε τις σταθερές ταχύτητες σε ευθεία γραμμή.
Η νέα θεωρία της βαρύτητας
Ενώ όμως οι εξισώσεις του ΜaxweΙΙ δεν χρειάζονται καμιά τροποποίηση γιατί ήδη ικανοποιούν και τις αρχές του Αϊνστάιν, ο νόμος της βαρύτητας έπρεπε να τροποποιηθεί γιατί είναι ασυμβίβαστος με τις αρχές αυτές.
Ο πιο απλός τρόπος να δούμε το ασυμβίβαστο είναι να επισημάνουμε το γεγονός ότι ο νόμος της παγκόσμιας έλξης συνεπάγεται ακαριαία μετάδοση των δυνάμεων, ενώ οι αρχές του Αϊνστάιν οδηγούν στο συμπέρασμα πως η ταχύτητα του φωτός είναι η μέγιστη.
Η νέα θεωρία βαρύτητας που προέκυψε για συμβιβάσει το πιό πάνω ασυμβίβαστο φέρει το όχι και τόσο αντιπροσωπευτικό όνομα της Γενικής Θεωρίας της Σχετικικότητας. Η νέα θεωρία είναι μοναδική από την άποψη της σαφήνειας, λιτότητας και κομψότητας κάνοντας τους Landau και Lifshitz, να την χαρακτηρίσουν σαν τη πιο όμορφη θεωρία της Φυσικής.
Βάση για τη νέα θεωρία είναι μια απλή παρατήρηση που έχουμε ήδη επισημάνει. Η μάζα παίζει ένα διπλό ρόλο. Είναι δημιουργός και δέκτης βαρυτικών δυνάμεων (όπως φαίνεται, από το νόμο της παγκόσμιας έλξης) αλλά συγχρόνως και μέτρο της αδράνειας των σωμάτων (από το νόμο F = ma).
Ακριβώς λόγω αυτής της σύμπτωσης που είναι γνωστή σαν αρχή της ισοδυναμίας – η ένταση του πεδίου βαρύτητας είναι ίση με την επιτάχυνση. Επομένως αντί να μελετήσουμε το πεδίο βαρύτητας μπορούμε ισοδύναμα να εξετάσουμε τι συμβαίνει σ’ ένα σύστημα που επιταχύνεται.
Ο Αϊνστάιν έκανε την επαναστατική υπόθεση πως η βαρύτητα είναι συνέπεια του γεγονότος ότι ο χωρόχρονος δεν είναι επίπεδος, όπως στην Ευκλείδεια Γεωμετρία, αλλά καμπύλος.
Η νέα θεωρία του δέχεται πως λόγω της μάζας ή ισοδύναμα όταν υπάρχει ενέργεια, η γεωμετρία του χώρου παύει να είναι ευκλείδεια. Στην ευκλείδεια γεωμετρία π.χ γνωρίζουμε πως το εμβαδόν της σφαιρικής επιφάνειας είναι S=4πr2 .
ή αν λύσουμε ως προς την ακτίνα ![]()
Όμως στη νέα θεωρία βαρύτητας ή όπως λέγεται Γενική Θεωρία της Σχετικότητας (ΓΘΣ), η διαφορά  δεν είναι μηδέν αλλά
δεν είναι μηδέν αλλά 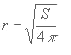 =Gm/3c2
=Gm/3c2
Η παραπάνω σχέση είναι η θεμελιώδης εξίσωση της βαρύτητας κατά Αϊνστάιν και συνδέει το αίτιο (δηλαδή τη μάζα m) με το αποτέλεσμα  , δηλαδή την απόκλιση από την ευκλείδεια γεωμετρία .
, δηλαδή την απόκλιση από την ευκλείδεια γεωμετρία .
Από τη τροποποιημένη γεωμετρία που έχουμε ήδη προσδιορίσει, μπορούμε να βρούμε τη τροχιά, που συμπίπτει:ι με τη γραμμή του ελάχιστου μήκους.
Η γραμμή όμως του ελάχιστου μήκους σε μια τροποποιημένη (μη ευκλείδεια) γεωμετρία δεν είναι η ευθεία γραμμή. Στην εποχή όμως του Αϊνστάιν υπήρχε ευτυχώς η κατάλληλη μη ευκλείδεια γεωμετρία, στην οποία η καμπύλη τροχιά συμπίπτει με τη γραμμή ελάχιστου μήκους.
Το σχήμα λοιπόν που πρότεινε ο Αϊνστάιν για τη θεωρία βαρύτητας μπορεί να συνοψισθεί ως εξής:
Η μάζα μέσω της εξίσωσης βαρύτητας οδηγεί σε μια μη Ευκλείδεια Γεωμετρία, στην οποία η καμπύλη τροχιά συμπίπτει με μια γραμμή ελάχιστου μήκους (γεωδαισιακή).
Την καμπυλότητα του χώρου την προκαλεί η παρουσία της ύλης, δηλαδή της μάζας (ή αν προτιμάτε της ενέργειας). Έτσι τα σώματα κινούνται όχι λόγω κάποιας βαρυτικής δύναμης αλλά κινούνται στις τροχιές του καμπύλου χωρόχρονου, που λέγονται γεωδαισιακές. Η γεωδαισιακή είναι η καμπύλη με το μικρότερο μήκος, όπως η ευθεία στον επίπεδο Ευκλείδειο χώρο.
Ένα βαρύ αντικείμενο, όπως ο Ήλιος προκαλεί καμπύλωση του χωρόχρονου.
Επειδή είναι δύσκολο να φανταστούμε τέσσερις διαστάσεις, οι φυσικοί συνήθως συνιστούν να σκεφτόμαστε το χωρόχρονο σαν ένα τεντωμένο, επίπεδο, ελαστικό φύλλο. Αν δεν υπάρχουν μεγάλες μάζες στην περιοχή, το φύλλο αυτό παραμένει επίπεδο, και κάθε σώμα που τοποθετείται πάνω σ΄ αυτό θα κινείται σε ευθεία γραμμή.
Αλλά μια μεγάλη μάζα όπως π.χ ο Ήλιος, δημιουργεί μια λακκούβα στο φύλλο αυτό γιατί στην πραγματικότητα καμπυλώνει τον χωρόχρονο. Κάθε άλλο αντικείμενο με μικρότερη μάζα, όπως π.χ η Γη, που κινείται στο χωρόχρονο κυλάει μέσα στην λακκούβα καθώς κινείται προς την περιοχή του Ήλιου. Κατ΄ αυτόν τον τρόπο μας δίνει την εντύπωση ότι έλκεται από την μεγάλη μάζα του Ήλιου. Αυτό το φαινόμενο της καμπύλωσης του χωροχρόνου είναι που γεννά τη βαρύτητα.
Πειραματικές δοκιμασίες
Για μικρές ταχύτητες (δηλαδή πολύ μικρότερες από τη ταχύτητα του φωτός) η θεωρία τείνει να δώσει ακριβώς τα ίδια συμπεράσματα με τη Νευτώνεια θεωρία.
Ο ίδιος ο Einstein πρότεινε τρία διαφορετικά πειραματικά τεστ, τα οποία η Γενική Θεωρία της Σχετικότητας πέρασε με επιτυχία.
Οι αρχικές όμως δοκιμασίες ήσαν πολύ περιορισμένες για να καθιερώσουν τη θεωρία. Τα τελευταία όμως 40 χρόνια με την εντυπωσιακή ανάπτυξη της αστροφυσικής και τη τεράστια βελτίωση της ακρίβειας των μετρήσεων μας, η Γενική θεωρία της Σχετικότητας έχει περάσει με επιτυχία πάρα πολλά τεστ.
1. Ένα επιτυχημένο παράδειγμα απόδειξης της Γ.Θ.Σ., είναι η στροφή του άξονα της έλλειψης της τροχιάς του Ερμή (που επειδή είναι ο πλησιέστερος πλανήτης στον Ήλιο, δέχεται ισχυρές βαρυτικές δυνάμεις), κατά 575 ” κάθε αιώνα.
Οι αστρονόμοι του 19ου αιώνα, με την Νευτώνεια Μηχανική εξήγησαν το μεγαλύτερο μέρος αυτής της ‘προπόρευσης του περιηλίου’ αλλά έμεναν ακόμη 43 ” να εξηγηθούν. Ο Αϊνστάιν την εξήγησε με βάση την Γ.Θ.Σ.
2.Το 1960, πέντε χρόνια μετά το θάνατο του Αϊνστάιν, όταν απέκτησαν οι επιστήμονες ρολόγια υψηλής ακριβείας (ατομικά ρολόγια), έγινε το εξής πείραμα. Εγκατέστησαν το ένα ρολόϊ στο υπόγειο ενός ουρανοξύστη και ένα άλλο στην κορυφή του. Τα ρολόγια ήταν απόλυτα συγχρονισμένα. Αλλά όμως το ρολόι του υπογείου εμφάνιζε μια επιβράδυνση σε σύγκριση με το άλλο της κορυφής, επειδή βρισκόταν βαθύτερα στο εσωτερικό του βαρυτικού πεδίου της Γης.
Το φως από ένα μακρινό αστέρι καμπυλώνει γύρω από εμπόδια στον χωρόχρονο.
3.Το Σύμπαν είναι γεμάτο από αντικείμενα μεγάλης μάζας που ασκούν βαρυτικές έλξεις. Τα αντικείμενα αυτά κάνουν το χωροχρόνο να μην είναι παντού τελείως επίπεδος αλλά καμπυλωμένος.
Κάθε τι συμπεριλαμβανομένου του φωτός, αναγκάζεται να ακολουθεί καμπυλωμένες τροχιές στον χωροχρόνο. Ενώ στην εποχή του, κανείς δεν γνώριζε για την καμπυλότητα του χώρου, σήμερα γνωρίζουμε ότι ο Einstein είχε δίκιο, διότι οι αστρονόμοι μερικές φορές παρατηρούν μακρινά αστέρια, που θα έπρεπε κανονικά να κρύβονται από κοντινότερα αντικείμενα όπως ο Ήλιος, αφού βρίσκονται σε ευθεία γραμμή πίσω του.
Αντί όμως να ταξιδεύει το φως του μακρινού άστρου σε ευθεία γραμμή, και να εμποδίζεται από το αντικείμενο που βρίσκεται μπροστά του, καμπυλώνεται η τροχιά του γύρω από το εμπόδιο και φτάνει έτσι στον παρατηρητή.
4.Άλλα πειραματικά τεστ για την επιβεβαίωση της ΓΘΣ, είναι το φαινόμενο των βαρυτικών φακών στην Αστρονομία.
Τα σμήνη των γαλαξιών, είναι τόσο ογκώδη και συμπαγή, που οι ακτίνες του φωτός που περνούν μέσω αυτών, εκτρέπονται από το τεράστιο βαρυτικό πεδίο τους, όπως ένας οπτικός φακός κάμπτει το φως διαμορφώνοντας έτσι μια εικόνα. Η διαδικασία αυτή ενισχύει, λαμπρύνει και διαστρεβλώνει τις εικόνες των αντικειμένων που βρίσκονται, σε αρκετά μεγάλη περιοχή από ένα σμήνος. Αυτό μας παρέχει έναν ισχυρό “ζουμάρισμα” για την όψη των γαλαξιών που είναι τόσο μακρυά, τέτοια που αυτοί δεν θα μπορούσαν να παρατηρηθούν κανονικά έστω με τα μεγαλύτερα διαθέσιμα τηλεσκόπια.
5. Οι Μαύρες Τρύπες άγνωστες μέχρι 30 χρόνια πριν, τα τελευταία χρόνια έχουν βρεθεί σε πολλά σημεία του Σύμπαντος, συνήθως στα κέντρα των Γαλαξιών ή σε ένα διπλό αστρικό σύστημα, με το ένα άστρο να έχει καταλήξει σε μαύρη τρύπα ‘καταπίνοντας’ αστρική ύλη από τον σύντροφό της.
![]() Σε μια Μαύρη Τρύπα, η μάζα είναι συγκεντρωμένη σε μια εξαιρετικά μικρή περιοχή με μια εξαιρετικά μεγάλη πυκνότητα. Αυτές ασκούν μια τεράστια ελκτική βαρυτική δύναμη στα άλλα αντικείμενα γύρω τους, ώστε τίποτε δεν μπορεί να διαφύγει από αυτές ούτε ακόμη και το φως. Τι ακριβώς όμως προκαλεί μια Μαύρη Τρύπα στο χωροχρόνο;
Σε μια Μαύρη Τρύπα, η μάζα είναι συγκεντρωμένη σε μια εξαιρετικά μικρή περιοχή με μια εξαιρετικά μεγάλη πυκνότητα. Αυτές ασκούν μια τεράστια ελκτική βαρυτική δύναμη στα άλλα αντικείμενα γύρω τους, ώστε τίποτε δεν μπορεί να διαφύγει από αυτές ούτε ακόμη και το φως. Τι ακριβώς όμως προκαλεί μια Μαύρη Τρύπα στο χωροχρόνο;
Η Γενική Σχετικότητα προβλέπει ότι το κέντρο μιας μαύρης τρύπας είναι ένα σημείο άπειρης πυκνότητας (μια χωροχρονική ανωμαλία) όπου οι συνηθισμένοι νόμοι της Φυσικής δεν ισχύουν πλέον. Ο χρόνος, ο χώρος, η ύλη και η ενέργεια δεν έχουν στην περιοχή μιας ανωμαλίας καλά καθορισμένο νόημα.
Οι εξισώσεις του Einstein δείχνουν ότι μια τέτοια ανωμαλία δεν προκαλεί απλά μια λακκούβα στο φανταστικό επίπεδο φύλλο του χωροχρόνου, αλλά δημιουργεί ένα τούνελ που τρυπάει το επίπεδο φύλλο και στιγμιαία μας συνδέει με την άλλη του πλευρά. Η πρώτη Μαύρη Τρύπα που ανακαλύφθηκε ήταν η Cygnus X-1, περίπου 7000 έτη φωτός από τη Γη το 1970.
Για την ειρωνεία, ο Αϊνστάιν δεν πίστευε στην ύπαρξη των μαύρων τρυπών, ακόμη κι αν προβλέπονταν από τη θεωρία του.
6. Ο νόμος της γενικής σχετικότητάς του, συμπεραίνει όμως ότι ο κόσμος πρέπει να καταρρεύσει κάτω από την τρομακτική ώθηση της βαρύτητας. Εντούτοις, όπως και πολλοί άλλοι επιστήμονες του καιρού του, ο Αϊνστάιν υπέθεσε πως το σύμπαν είναι στατικό και αμετάβλητο.
Για να μπορέσει να περιγράψει όμως ένα σταθερό σύμπαν, ο Αϊνστάιν πρόσθεσε κάτι στις εξισώσεις της Γ.Θ.Σ., που το ονόμασε “κοσμολογική σταθερά”, μια απωστική δύναμη ή αρνητική βαρύτητα, αν και δεν είχε καμία ιδέα εάν ήταν πραγματική. Αναγκάστηκε όμως να την αφαιρέσει από τις εξισώσεις λέγοντας πως ήταν το μεγαλύτερο λάθος του.
Η σταθερά αυτή λ, αντιπροσωπεύει μια απωστική συμπαντική δύναμη, εξαρτώμενη από το ίδιο το διάστημα, και η οποία εμποδίζει το σύμπαν να καταρρεύσει (να συσταλεί) κάτω από την επίδραση της βαρύτητας.
Σήμερα γνωρίζουμε πως πράγματι το Σύμπαν διαρκώς επεκτείνεται, σύμφωνα με το νόμο του Hubble και την ερυθρή μετατόπιση, και μάλλον δεν πρόκειται ποτέ να συνθλιβεί.
7.Άλλα αστρονομικά αντικείμενα που εξάπτουν τη φαντασία, είναι όπως γνωρίζουμε οι “σκουληκότρυπες”. Μπορούν δε θεωρητικά να λειτουργήσουν σαν ένα είδος συντόμευσης ανάμεσα σε δύο απομακρυσμένα σημεία στο Σύμπαντος και βασίζονται στη Γενική Θεωρία της Σχετικότητας, που σύμφωνα με αυτήν μόνο “σκουληκότρυπες” μικροσκοπικού μεγέθους είναι δυνατόν να υπάρξουν.
8..Ξεκινώντας το 1917, ο Αϊνστάιν και άλλοι επιστήμονες, εφάρμοσαν τη Γενική Σχετικότητα στη δομή και την εξέλιξη του σύμπαντος θεωρώντας το σαν όλον. Η κοσμολογική θεωρία που προέκυψε, ήταν η θεωρία της Μεγάλης Έκρηξης ή Big Bang, που σχηματίσθηκε το 1922 από τον Ρώσο μαθηματικό και μετεωρολόγο Alexander Friedmann. Ο Friedmann ξεκίνησε με τις εξισώσεις της Γ.Θ.Σ. και βρήκε μια λύση σε αυτές τις εξισώσεις στην οποία το Σύμπαν ξεκίνησε με μια κατάσταση εξαιρετικά υψηλής πυκνότητας και θερμοκρασίας. Από τότε διαστέλλεται στον χρόνο, συνεχώς ψυχόμενο.
9..Ένα άλλο φαινόμενο, που εξηγείται με την Γ.Θ.Σ. είναι η βαρυτική μετατόπιση προς το ερυθρό. Σύμφωνα με τη Θεωρία, το μήκος κύματος του φωτός ή μιας Η/Μ ακτινοβολίας, που περνά μέσω ενός ισχυρού βαρυτικού πεδίου μετατοπίζεται προς την ερυθρή περιοχή του φάσματος. Τα φωτόνια επειδή προσπαθούν να ξεφύγουν από το βαρυτικό πεδίο, χάνουν ενέργεια άρα θα πρέπει η συχνότητα τους να μειώνεται ή ισοδύναμα το μήκος τους λ να αυξάνεται. Πειράματα τέτοια έγιναν πολλά. Κοντά στη Γη το 1960 από τους Robert V. Pound και Glen A. Rebka και για την μετατόπιση προς το ερυθρό του φωτός του Ήλιου, πάλι το 1960 από μια ομάδα του Πανεπιστημίου Princeton.
Κύματα βαρύτητας
Υπάρχει όμως ένα πολύ σημαντικό τεστ που δεν έχουμε καταφέρει ακόμα να πραγματοποιήσουμε. Δεν έχει ακόμα διαπιστωθεί πειραματικά η ύπαρξη κυμάτων βαρύτητας.
Μια και η θεωρία της βαρύτητας του Αϊνστάιν ικανοποιεί τη βασική αρχή για το αναλλοίωτο της ταχύτητας του φωτός έπεται ότι η βαρυτική δύναμη (όπως άλλωστε και η ηλεκτρομαγνητική) μεταδίδεται με πεπερασμένη ταχύτητα όχι μεγαλύτερη από τη ταχύτητα του φωτός, με τη μορφή βαρυτικού κύματος.
Η Γενική θεωρία της Σχετικότητας προβλέπει την ύπαρξη κυμάτων βαρύτητας. Η πειραματική όμως διαπίστωση της ύπαρξης των κυμάτων αυτών είναι πολύ δύσκολη και δεν έχει επιτευχθεί μέχρι σήμερα παρ’ όλες τις προσπάθειες και τις κατά καιρούς θετικές ενδείξεις. Η μεγάλη δυσκολία πηγάζει από το ότι η δύναμη βαρύτητας είναι πολύ ασθενής, επομένως και τα κύματα βαρύτητας μεταφέρουν πολύ λίγη ενέργεια πράγμα που τα κάνει να περνούν απαρατήρητα.
Τέλος στην θεωρία βαρύτητας του Αϊνστάιν το σχήμα που χρησιμοποιείται για τη περιγραφή της βαρύτητας (μάζα – γεωμετρία – τροχιά) είναι διαφορετικό από εκείνο που χρησιμοποιείται στον Ηλεκτρομαγνητισμό (φορτίο – δυνάμεις – τροχιά).
Αν μπορούσαμε να εντάξουμε τον ηλεκτρομαγνητισμό στο ίδιο σχήμα με τη βαρύτητα, ώστε να έχουμε μια ενοποιημένη περιγραφή των θεμελιακών σχέσεων του κόσμου μας, τότε κατασκευάζαμε ένα ενοποιημένο σχήμα της μορφής
μάζα και φορτίο – γεωμετρία – τροχιά.
Είναι αλήθεια πως ο Αϊνστάιν ξόδεψε τα τελευταία 35 χρόνια της ζωής του προσπαθώντας να πετύχει μια τέτοια θεμελιακή ενοποίηση. Δεν τα κατάφερε.





