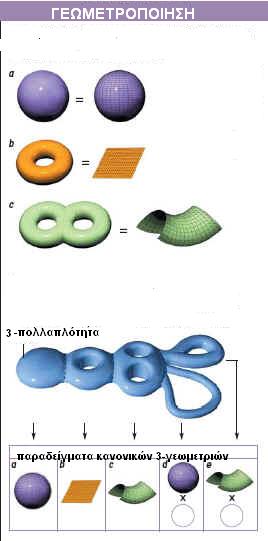
Οι 2-πολλαπλότητες μπορούν να ταξινομηθούν με την γεωμετροποίησή τους. Αυτό σημαίνει να τους αποδώσουμε μια ειδική γεωμετρία δηλαδή να τις αντιστοιχίσουμε σ' ένα στερεό σχήμα. Πιο συγκεκριμένα, καθεμιά μπορεί να μορφοποιηθεί σε ένα σχήμα που έχει παντού την ίδια καμπυλότητα επάνω του. Η σφαίρα [α] είναι το μοναδικό σχήμα που έχει σταθερή, θετική καμπυλότητα, δηλαδή σε κάθε της σημείο είναι καμπυλωμένη όπως η κορυφή ενός λόφου. Ο τόρος [b] μπορεί να γίνει επίπεδος, δηλαδή με μηδενική καμπυλότητα σε όλη του την έκταση. Για να το καταλάβουμε αυτό, φαντασθείτε ότι μπορούμε να κατασκευάσουμε ένα τόρο αν ξεκινήσουμε από ένα ορθογώνιο παραλληλόγραμμο και σχηματίσουμε συγχρόνως δύο κυλίνδρους τυλίγοντάς τον ώστε να  κολλήσουμε συγχρόνως ανά δύο τις απέναντι πλευρές του. Ο τόρος έχει έτσι απεικονιστεί σε ένα επίπεδο σχήμα.

Επιφάνειες τύπου-2 και ανώτερες [c], μπορούν να έχουν σταθερή αρνητική καμπυλότητα, ενώ οι άλλες λεπτομέρειές τους εξαρτώνται από το πόσες λαβές έχουν. Εδώ η επίφάνεια με σταθερή αρνητική καμπυλότητα παριστάνεται με το σχήμα σέλας. 

Η ταξινόμηση των 3-πολλαπλοτήτων, η οποία είναι όμοια με αυτή των 2-πολλαπλοτήτων, αλλά πολύ περισσότερο περίπλοκη, συμπληρώθηκε με την εργασία του Perelman. Γενικά, μια 3-πολλαπλότητα πρέπει να διαιρεθεί σε τμήματα, καθένα από τα οποία μπορεί να μορφοποιηθεί σε μια από οκτώ διαφορετικές κανονικές 3-διάστατες γεωμετρίες. Το παρακάτω παράδειγμα με μπλε χρώμα (το οποίο για σχεδιαστικούς λόγους έχει αποδοθεί σαν 2-πολλαπλότητα, ) αποτελείται από ισοδύναμες με πέντε εξ αυτών των γεωμετριών: σταθερή θετική [α], μηδενική [b], και σταθερή αρνητική καμπυλότητα [c], καθώς και από το "γινόμενο" της 2-σφαίρας και ενός κύκλου [d], και από το γινόμενο της επιφάνειας αρνητικής καμπυλότητας και ενός κύκλου [e].  

Πως όμως θα μπορούσαμε να γεωμετροποιήσουμε μια πολλαπλότητα - να της δώσουμε δηλαδή μια ομοιόμορφη καμπυλότητα σε όλη της την έκταση; Ένας τρόπος είναι να ξεκινήσουμε με μια αυθαίρετη γεωμετρία, κάτι σαν ένα αυγοειδές σχήμα με διάφορα εξογκώματα και βυθίσεις, και στη συνέχεια να εξομαλύνουμε όλες τις ανωμαλίες. Ο Hamilton άρχισε ένα τέτοιο πρόγραμμα ανάλυσης για τις 3-πολλαπλότητες, στο τέλος της δεκαετίας του 1990, χρησιμοποιώντας μια εξίσωση που λέγεται εξίσωση ροής του Ricci, (από τον μαθηματικό Gregorio Ricci-Curbastro), η οποία έχει κάποιες ομοιότητες με την εξίσωση που περιγράφει τη ροή θερμότητας. Σε ένα σώμα με θερμά και ψυχρά σημεία, η θερμότητα φυσικά ρέει από τα θερμότερα προς τα ψυχρότερα σημεία, ώσπου να αποκατασταθεί μια ομοιόμορφη θερμοκρασία παντού. Η εξίσωση ροής του Ricci έχει ένα όμοιο αποτέλεσμα στην καμπυλότητα, μορφοποιώντας μια πολλαπλότητα, ώσπου να εξαφανίσει όλα τα εξογκώματα και τις κοιλότητες. Αν ξεκινήσουμε με ένα αυγό, θα καταλήξει στο τέλος να είναι τέλεια σφαίρα. 

Η ανάλυση του Ηamilton προσέκρουσε όμως σε ένα εμπόδιο: Σε μερικές περιπτώσεις, η ροή του Ricci θα έκανε μια πολλαπλότητα να καταλήξει σε ένα σημείο. Αυτή είναι μια περίπτωση όπου η ροή του Ricci διαφέρει από τη ροή θερμότητας. Τα μέρη όπου συμβαίνει αυτή η κατάληξη σε σημεία, είναι σαν να φτάνουμε με τηροή θερμότητας σε σημεία όπου έχουμε άπειρη θερμοκρασία.
Ένα τέτοιο παράδειγμα ήταν όταν η πολλαπλότητα είχε σχήμα αλτήρα (σαν δύο σφαίρες συνδεδεμένες με ένα λεπτό σύνδεσμο). Οι σφαίρες θα μεγάλωναν, αντλώντας προοδευτικά ύλη από τον σύνδεσμο, ο οποίος θα κατέληγε σε ένα σημείο στο μέσον. (βλέπε παρακάτω σχήμα). 
Ένα άλλο παράδειγμα προέκυπτε όταν μια λεπτή ράβδος προεξείχε από την πολλαπλότητα. Η ροή του Ricci μπορούσε να προκαλέσει τότε ένα πρόβλημα που λέγεται ανωμαλία πούρου.
Όταν μια πολλαπλότητα οδηγείται σε τέτοιες καταρρεύσεις, λέγεται ανωμαλία. Δεν είναι πια μια πραγματική 3-διάστατη πολλαπλότητα. Σε μια πραγματική 3-διάστατη πολλαπλότητα, μια μικρή περιοχή γύρω από οποιοδήποτε σημείο, μοιάζει με μια μικρή περιοχή συνηθισμένου 3-διάστατου χώρου, αλλά η ιδιότητα αυτή δεν ισχύει στα στενώματα. Ένας τρόπος ξεπεράσματος αυτού του εμποδίου υποδείχτηκε από τον Perelman. 

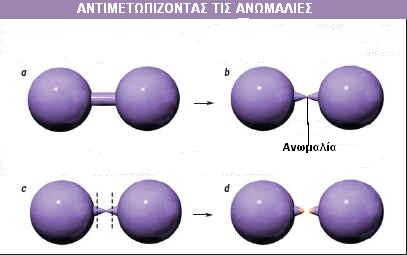
Οι προσπάθειες να εφαρμόσουμε μια εξίσωση που λέγεται ροή του Ricci για να αποδείξουμε την εικασία του Poincaré και να γεωμετροποιήσουμε τις 3-πολλαπλότητες, προσέκρουσε σε ένα εμπόδιο πριν από την εμφάνιση του Perelman. Η ροή του Ricci, η οποία βαθμιαία αλλάζει το σχήμα μιας 3-πολλαπλότητας, μερικές φορές δεν δουλεύει γιατί φτάνει σε ανωμαλίες. Μια τέτοια περίπτωση είναι όταν μέρος της πολλαπλότητας έχει σχήμα αλτήρα - δύο σφαίρες συνδεδεμένες με ένα λεπτό σωλήνα [α]. Ο σωλήνας μπορεί να στενέψει και να καταλήξει σε σημείο, καταστρέφοντας τις ιδιότητες της πολλαπλότητας [b]. Μια άλλη ανωμαλία, που πιστεύαμε ότι θα μπορούσε να συμβεί, ήταν η λεγόμενη ανωμαλία πούρου. 
Μια "χειρουργική μέθοδος" θα μπορούσε να διαχειριστεί τις ανωμαλίες που προκύπτουν κατά τη ροή του Ricci, όπως έδειξαν οι εργασίες του Perelman. Όταν μια περιοχή της πολλαπλότητας αρχίζει να στενεύει, μια μικρή περιοχή από κάθε πλευρά της στένωσης μπορεί να αποκοπεί [c]. Τα κοψίματα καλύπτονται τότε από μικρές σφαίρες, και η ροή του Ricci συνεχίζεται [d]. Η διαδικασία αυτή μπορεί να χρειαστεί να επαναληφθεί αρκετές φορές σε άλλες περιοχές που παρουσιάζεται στένωμα, αλλά ο Perelman έδειξε ότι τελικά η διαδικασία τερματίζεται κάποτε. Έδειξε επίσης ότι οι ανωμαλίες τύπου πούρου δεν εμφανίζονται ποτέ.   

Όταν ο Perelman πρωτοπήγε στις ΗΠΑ σαν μεταπτυχιακός σπουδαστής το 1992, δημιούργησε  γρήγορα μια φήμη ταλαντούχου μαθηματικού, καθώς απέδειξε πολλά σημαντικά και βαθιά αποτελέσματα στη γεωμετρία. Το 1995 του προσφέρθηκαν θέσεις σε αρκετά σημαντικά τμήματα μαθηματικών, αλλά τα απέρριψε και προτίμησε να επιστρέψει στην Αγία Πετρούπολη. Πίσω στη χώρα του, ουσιαστικά εξαφανίστηκε από τη διεθνή κοινότητα των μαθηματικών. Τα μόνα σημάδια της ύπαρξής του ήταν όταν έστελνε κάποια μηνύματα μέσω του internet για να τους υποδείξει λάθη που υπήρχαν στις δημοσιεύσεις τους που έκαναν στο διαδίκτυο. 
Τέλος το 2002, αρκετοί συνάδελφοί του πήραν ένα e-mail με το οποίο τους καλούσε να δουν την εργασία που μόλις είχε δημοσιεύσει στο διαδίκτυο. Η δημοσίευση αυτή ήταν το πρώτο στάδιο της επίθεσής του στο πρόβλημα του Poincaré.
Στην εργασία του αυτή ο Perelman πρόσθετε έναν ακόμη όρο στην εξίσωση ροής του Ricci. Η τροποποιημένη εξίσωση δεν εξαλείφει τα προβλήματα με τις ανωμαλίες, αλλά αλλά μ' αυτή μπόρεσε να προχωρήσει την ανάλυση αρκετά μακρύτερα. Για τις ανωμαλίες του αλτήρα, έδειξε ότι θα μπορούσε να χρησιμοποιηθεί η "χειρουργική τεχνική". Αποκόπτουμε δηλαδή τον λεπτό σωλήνα σε κάθε πλευρά του στενώματος και κλείνουμε τον λεπτό σωλήνα στα σημεία που τον κόβουμε με ένα σφαιρικό καπάκι. Τότε η ροή του Ricci μπορεί να συνεχιστεί στην τροποποιημένη πολλαπλότητα μέχρι να συναντήσουμε το επόμενο στένωμα, όπου θα ακολουθήσουμε την ίδια μέθοδο. Έδειξε επίσης ότι οι ανωμαλίες τύπου πούρου δεν μπορούσαν να εμφανιστούν. Με τον τρόπο αυτό, κάθε 3-πολλαπλότητα μπορούσε να αναχθεί σε ένα σύνολο κομματιών που το καθένα θα είχε μια ομοιόμορφη γεωμετρία.

Όταν η ροή του Ricci και η χειρουργική τεχνική εφαρμόζονταν σε κάθε δυνατή πολλαπλότητα, κάθε πολλαπλότητα που είναι τόσο απλή όσο η 3-σφαίρα, αναγκαστικά καταλήγει με την ίδια ομοιόμορφη γεωμετρία σαν αυτή της 3-σφαίρας. Αυτό το αποτέλεσμα σημαίνει ότι τοπολογικά, η συγκεκριμένη πολλαπλότητα είναι μια 3-σφαίρα. Με άλλα λόγια η 3-σφαίρα είναι μοναδική.  

Πέρα από την απόδειξη της εικασίας του Poincaré, η έρευνα του Perelman είναι σημαντική και για τις καινούργιες μεθόδους ανάλυσης που εισήγαγε. Ήδη οι μαθηματικοί κάνουν δημοσιεύσεις στηριζόμενοι στη δουλειά του, ή εφαρμόζουν. Επιπρόσθετα, τα μαθηματικά έχουν περίεργες διασυνδέσεις με τη φυσική. Η ροή του Ricci όπως χρησιμοποιήθηκε από τους Hamilton και Perelman σχετίζεται με αυτό που αποκαλείται ομάδα επανακανονικοποίησης, και η οποία καθορίζει πως μεταβάλλεται η ισχύς των αλληλεπιδράσεων με την ενέργεια των σωματίων που συγκρούονται. Για παράδειγμα, στις χαμηλές ενέργειες η ηλεκτρομαγνητική αλληλεπίδραση έχει ισχύ που χαρακτηρίζεται από τον αριθμό 0,0073 (περίπου 1/137). Αν δύο ηλεκτρόνια συγκρουστούν κεντρικά καθώς τρέχουν σχεδόν με την ταχύτητα του φωτός, η ένταση της αλληλεπίδρασης χαρακτηρίζεται μάλλον από την τιμή 0,0078.
Το να αυξάνουμε την ενέργεια της σύγκρουσης είναι ισοδύναμο με το να μελετάμε τη δύναμη σε όλο και πιο μικρή κλίμακα αποστάσεων. Η ομάδα επανακανονικοποίησης είναι συνεπώς σαν ένα μικροσκόπιο με μεγέθυνση που μπορεί να αυξηθεί ή να μειωθεί προκειμένου να εξετάσουμε μια διαδικασία με μεγαλύτερη ή μικρότερη λεπτομέρεια. 
Παρόμοια, η ροή του Ricci είναι σαν ένα μικροσκόπιο για να κοιτάξουμε σε μια πολλαπλότητα με μια μεγέθυνση της επιλογής μας. Εξογκώματα και κοιλότητες, ορατά σε μια μεγέθυνση, εξαφανίζονται σε μια άλλη. Οι φυσικοί αναμένουν ότι σε μια κλίμακα περίπου 10^-35 μέτρα, (μήκος Planck), ο χώρος στον οποίο ζούμε θα μοιάζει πολύ διαφορετικός από αυτόν που αισθανόμαστε άμεσα. Συγκεκριμένα αναμένουμε ότι θα μοιάζει με έναν "αφρό" με πολλούς βρόχους και λαβές και άλλες τοπολογικές δομές. Τα μαθηματικά που περιγράφουν πως μεταβάλλονται οι φυσικές δυνάμεις, είναι τελείως όμοια με αυτά που περιγράφουν την γεωμετροποίηση μιας πολλαπλότητας.

Μια άλλη σύνδεση με τη φυσική, είναι ότι οι εξισώσεις της γενικής σχετικότητας σχετίζονται στενά με την εξίσωση ροής του Ricci. Ακόμα παραπέρα, ο όρος που πρόσθεσε ο Perelman στην εξίσωση ροής του Ricci, εμφανίζεται στη θεωρία χορδών, η οποία φιλοδοξεί να είναι μια κβαντική θεωρία της βαρύτητας. Περιμένουμε να δούμε αν οι τεχνικές του Perelman θα αποκαλύψουν νέες ενδιαφέρουσες πληροφορίες για τη γενική σχετικότητα ή για τη θεωρία χορδών. Αν συμβεί κάτι τέτοιο, ο Perelman δεν θα μας έχει διδάξει μόνο για τα σχήματα των αφηρημένων 3-χώρων, αλλά επίσης και για τη μορφή του χώρου εντός του οποίου ζούμε.   

Μια συνάθροιση σοφών του περασμένου αιώνα στην πρώτη συνάντηση του Solvay, το 1911. Καθισμένοι ο Poincaré και η Marie Curie. Όρθιοι στέκονται από αριστερά οι Ernest Rutherford, Kamerlingh Onnes και Albert Einstein

1o, 2ο, 3ο