

 |
 |
Πως ερμηνεύεται η ηλεκτροστατική έλξη και άπωση με ανταλλαγή φωτονίων;Συχνές Ερωτήσεις, Φεβρουάριος 2003 |
|
Είναι γνωστό ότι μεταξύ των φορτισμένων σωματιδίων υπάρχει ελκτική ή απωστική δύναμη, που μεταβάλλεται αντιστρόφως ανάλογα με το τετράγωνο της απόστασης μεταξύ των σωματιδίων. Στα πλαίσια της σύγχρονης κβαντικής ηλεκτροδυναμικής, η δύναμη αυτή γίνεται κατανοητή με ανταλλαγή «εν δυνάμει» φωτονίων μεταξύ των φορτισμένων σωματιδίων. Η αλληλεπίδραση αυτή εκδηλώνεται με τη μεταβολή της ορμής των σωματιδίων, και τα φωτόνια είναι αυτά που μεταφέρουν την ορμή από το ένα στο άλλο. Παρακάτω εμφανίζεται ένα διάγραμμα Feynman που απεικονίζει μια ανταλλαγή ενός εν δυνάμει φωτονίου. 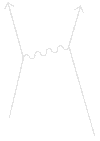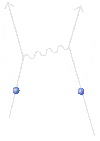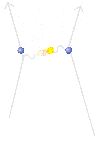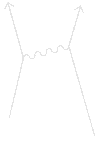  Οι γραμμές αριστερά παριστάνουν δύο φορτισμένα σωμάτια, και η κυματιστή γραμμή είναι ένα εν δυνάμει φωτόνιο που μεταφέρει ορμή από το ένα στο άλλο. Το σωματίδιο που εκπέμπει το φωτόνιο, χάνει ορμή και ανακρούεται προς τα πίσω, ενώ το άλλο σωματίδιο κερδίζει ορμή. Στην παραπάνω εικόνα της αλληλεπίδρασης δεν πρέπει να θεωρούμε το φωτόνιο που ανταλλάσσεται σαν μια σφαίρα. Τα εν δυνάμει σωματίδια δεν συμπεριφέρονται σαν κλασσικές σφαίρες. Το βασικότερο πρόβλημα του παραπάνω μοντέλου είναι ότι δεν μπορεί να εξηγήσει την ελκτική δύναμη. Αν σας πετάξω μια μπάλα, η ανάκρουση με σπρώχνει προς τα πίσω, αλλά κι εσείς όταν πιάσετε την μπάλα θα απωθηθείτε μακριά μου. Πως λοιπόν μπορεί η ρίψη μιας μπάλας μεταξύ μας να οδηγήσει σε ελκτική δύναμη; Μια κλασσική μπάλα δεν μπορεί να το κάνει αυτό. Μόνο η αρχή απροσδιοριστίας του Heisenberg για τον κβαντικό κόσμο μπορεί να εξηγήσει μια ελκτική δύναμη. Ας υποθέσουμε ότι δύο καλά εντοπισμένα στο χώρο σωματίδια ανταλλάσσουν ένα εν δυνάμει φωτόνιο ορμής p. Η αρχή απροσδιοριστίας μας λέει ότι μια συγκεκριμένη ορμή σχετίζεται με μια τεράστια απροσδιοριστία στη θέση. Ένα εν δυνάμει φωτόνιο ορμής p, αντιστοιχεί μ’ ένα επίπεδο κύμα που γεμίζει όλο το χώρο χωρίς να βρίσκεται σε κάποια συγκεκριμένη θέση. Δεν παίζει ρόλο ποια είναι η κατεύθυνση της ορμής, αυτή απλώς καθορίζει τον προσανατολισμό των μετώπων κύματος. Η φορά διάδοσης του κύματος μπορεί να είναι είτε από το σωματίδιο που το εξέπεμψε προς το σωματίδιο που το απορροφά, είτε από το άπειρο προς το σωματίδιο που το απορροφά και προς εκείνο που το εκπέμπει. Αφού το κύμα βρίσκεται παντού, το φωτόνιο μπορεί να δημιουργηθεί από το ένα σωματίδιο και να απορροφηθεί από το άλλο, όπου και αν βρίσκονται αυτά. Αν λοιπόν το κύμα συναντήσει το σωματίδιο που θα το απορροφήσει, με κατεύθυνση από το σωματίδιο που απορροφά προς το σωματίδιο που το εξέπεμψε, το αποτέλεσμα θα είναι μια ελκτική δύναμη μεταξύ τους. Από τα παραπάνω καταλαβαίνουμε λοιπόν γιατί δεν πρέπει οι γραμμές σ’ ένα διάγραμμα Feynman να ερμηνεύονται σαν τροχιές κλασσικών σωματιδίων. Στη συνέχεια μάλιστα θα εξετάσουμε μια ακόμη πιο περιορισμένη κατηγορία φαινομένων, στην οποία τα δύο φορτισμένα σωματίδια που αλληλεπιδρούν δεν είναι καλά εντοπισμένα στο χώρο, αλλά αντίθετα έχουν και αυτά μια απροσδιοριστία στη θέση τους. Τώρα όμως προβάλλει φυσιολογικά
ένα νέο ερώτημα: Ας εξετάσουμε το ζήτημα με όρους της κβαντομηχανικής. Ας υποθέσουμε για απλούστευση
ότι οι αρχικές κυματοσυναρτήσεις των
φορτισμένων σωματιδίων είναι
Γκαουσιανές σε ηρεμία, δηλαδή
πραγματικές συναρτήσεις σχήματος
καμπάνας, η μια μετά την άλλη πάνω στον
άξονα x. Ας θυμόμαστε πάντα ότι το
τετράγωνο αυτών των συναρτήσεων μας
δίνει την πιθανότητα να βρούμε το
σωματίδιο στην αντίστοιχη θέση του
άξονα x. Σχηματικά μοιάζουν κάπως έτσι:  Ας συγκεντρώσουμε την προσοχή μας σε ένα από τα σωματίδια. Ας πούμε σε αυτό που βρίσκεται αριστερά. Όπως υπάρχει η συνηθισμένη κυματοσυνάρτηση που είναι συνάρτηση της θέσης, έτσι στο «χώρο των ορμών», ορίζεται μια αντίστοιχη συνάρτηση για το σωματίδιο αυτό. Το τετράγωνο αυτής της συνάρτησης της ορμής, δίνει την αντίστοιχη πιθανότητα να έχει το σωματίδιό μας την αντίστοιχη ορμή. Αν η κυματοσυνάρηση στο συνηθισμένο χώρο είναι Γκαουσιανή, τότε και η κυματοσυνάρτηση στο χώρο των ορμών αποδεικνύεται επίσης ότι έχει τη μορφή μιας καμπύλης Γκάους. Η μορφή της φαίνεται στο παρακάτω σχήμα. όσο πιο στενή είναι η κυματοσυνάρτηση στο χώρο των θέσεων, τόσο πιο πλατιά θα είναι η αντίστοιχη Γκαουσιανή στο χώρο των ορμών. Αυτό απλά σημαίνει ότι όσο πιο καλά καθορισμένη είναι η θέση του σωματιδίου, τόσο πιο μεγάλη απροσδιοριστία υπάρχει στην ορμή του.  Για να απλοποιήσουμε το πρόβλημα θεωρούμε ότι η συνάρτηση στο χώρο των ορμών δεν είναι πολύ διευρυμένη όσον αφορά τις τιμές του p. Δηλαδή με άλλα λόγια η κυματοσυνάρτηση στο χώρο των θέσεων x, δεν είναι πάρα πολύ στενή. Κάτι τέτοιο μας επιτρέπει να αγνοήσουμε τα σχετικιστικά κβαντομηχανικά φαινόμενα. Προκειμένου για ηλεκτρόνια, η ρελατιβιστική όψη τους δεν εκδηλώνεται μέχρις ότου η κυματοσυνάρτηση θέσης συμπιεστεί τόσο ώστε να γίνει το εύρος της μικρότερο από τις διαστάσεις του ατόμου. Για σωματίδια με μεγαλύτερη μάζα το εύρος της κυματοσυνάρτησης πρέπει να περιοριστεί ακόμα πιο πολύ για να χρειαστεί να ληφθούν υπ όψιν σχετικιστικά φαινόμενα. Επίσης θα αγνοήσουμε τις μαγνητικές ροπές των σωματιδίων, διότι στην παρούσα εξέταση μας ενδιαφέρει μόνο η ηλεκτροστατική αλληλεπίδρασή τους. Ας θεωρήσουμε τώρα ένα εν δυνάμει φωτόνιο, που εκπέμπεται από το σωματίδιο στα δεξιά και απορροφάται από το σωματίδιο στ’ αριστερά. Επειδή η κβαντική ηλεκτροδυναμική προβλέπει ότι στον υπολογισμό των πλατών πιθανότητας για ανταλλαγή ενός φωτονίου πρέπει να ληφθεί υπ όψιν και η περίπτωση όπου το φωτόνιο εκπέμπεται μεν από το σωματίδιο στα δεξιά αλλά σε κάποια μελλοντική στιγμή και ταξιδεύει προς τα πίσω στο χρόνο μέχρι ν’ απορροφηθεί από το σωματίδιο στ’ αριστερά. Στη περίπτωση αυτή η ορμή του φωτονίου έχει αντίθετο πρόσημο απ’ αυτό που είχε η απλή εκπομπή από το δεξιό σωματίδιο και απορρόφηση αργότερα από το αριστερό σωματίδιο. Όταν ληφθούν υπ όψιν και οι δύο αυτές περιπτώσεις για το φωτόνιο, αποδεικνύεται ότι η κυματοσυνάρτησή του στο χώρο των ορμών προσεγγίζεται ως εξής: Έχουμε μια συνάρτηση ανάλογη με το ηλεκτρικό φορτίο του σωματιδίου που το εξέπεμψε. Εδώ ακριβώς έχουμε τον επηρεασμό από το είδος του φορτίου του εκπέμποντος σωματιδίου. Η κυματοσυνάρτηση αυτή έχει μερικές οξείες και στενές κορυφές. Η μία κορυφή είναι ανάλογη με -¡ φορές το φορτίο και βρίσκεται αριστερά του μηδενός στον άξονα των p. Η άλλη κορυφή έχει αντίθετο πρόσημο από την πρώτη και βρίσκεται δεξιά του μηδενός στον άξονα των p. Η μιγαδική συνιστώσα της κυματοσυνάρτησης του φωτονίου στο χώρο των ορμών έχει την παρακάτω μορφή, αν το σωματίδιο που το εξέπεμψε είναι αρνητικό.  Αν το σωματίδιο που εξέπεμψε το φωτόνιο ήταν θετικό τότε η κυματοσυνάρτηση θα είναι ανεστραμμένη ως προς τον άξονα των p. Το αποτέλεσμα τώρα της απορρόφησης του εν δυνάμει φωτονίου από το δεύτερο φορτισμένο σωματίδιο στ’ αριστερά, προκύπτει από μερικούς απλούς κανόνες της κβαντικής ηλεκτροδυναμικής. Υπάρχει ένα συγκεκριμένο πλάτος πιθανότητας να συναντήσει το φωτόνιο το σωμάτιο που θα το απορροφήσει ερχόμενο από τα δεξιά και ένα πλάτος πιθανότητας να το συναντήσει ερχόμενο από τ’ αριστερά. Το πλάτος πιθανότητας για κάθε δυνατότητα είναι ανάλογο προς το γινόμενο: i ٠ (φορτίο του σωματιδίου που απορροφά) ٠ (τιμή της συνάρτησης του φωτονίου) ٠ χρόνο. Οι υπόλοιπες σταθερές της αναλογίας εξαρτώνται από το σύστημα μονάδων, και για ποιοτικούς υπολογισμούς όπως αυτός που κάνουμε τώρα δεν θα μας απασχολήσουν. Στη συνέχεια για να βρούμε το ολικό πλάτος πιθανότητας για να συμβεί η απορρόφηση, πολλαπλασιάζουμε την αρχική κυματοσυνάρτηση του φορτισμένου σωματιδίου, μετατοπισμένη προς τα δεξιά ή αριστερά στον άξονα των ορμών, -ανάλογα με την κατεύθυνση από την οποία χτυπήθηκε από το φωτόνιο- επί το πλάτος της πιθανότητας που βρήκαμε πριν, ξεχωριστά για καθεμιά από τις δύο δυνατότητες και τέλος προσθέτουμε τις τελικές τιμές που προέκυψαν για τις δύο δυνατότητες. Αν και τα δύο σωμάτια είναι αρνητικά φορτισμένα, ή και τα δύο θετικά φορτισμένα, τότε προσθέτουμε μια προς τα αριστερά μετατοπισμένη θετική κυματοσυνάρτηση, με μια ανεστραμμένη προς τα κάτω και μετατοπισμένη προς τα δεξιά. Το αποτέλεσμα είναι μια πραγματική κυματοσυνάρτηση, και μοιάζει κάπως έτσι:
 Αν
τα δύο φορτία έχουν αντίθετα φορτία,
τότε η τελική εικόνα της
κυματοσυνάρτησης που θα προκύψει θα
είναι η αντεστραμμένη μορφή της
παραπάνω εικόνας που σχεδιάσαμε. Στο σημείο αυτό μπορεί κάποιος δικαιολογημένα να αναρωτηθεί: -
Παίρνουμε πιθανότητες υψώνοντας στο
τετράγωνο πλάτη πιθανότητας. Αν λοιπόν
υψώσουμε στο τετράγωνο την τελική
μορφή που βρήκαμε, δεν θα πάρουμε ως
αποτέλεσμα ότι η πιθανότητα να
μεταδοθεί ορμή προς το χτυπημένο
σωμάτιο η οποία θα το ωθήσει προς το
άλλο σωμάτιο, είναι ακριβώς ίση με την
πιθανότητα να το απομακρύνει από αυτό; Η απάντηση είναι: Όχι. Διότι οι κανόνες του Feynman της κβαντικής ηλεκτροδυναμικής λένε ότι υπάρχει ακόμα ένα πλάτος πιθανότητας για την εξέλιξη των γεγονότων που δεν το λάβαμε υπ’ όψιν. Το πλάτος αυτό περιγράφει την δυνατότητα να μην έχει συμβεί καμιά ανταλλαγή φωτονίου, και επειδή η δυνατότητα αυτή είναι απολύτως ισότιμη με την προηγούμενη της ανταλλαγής του φωτονίου, πρέπει η κυματοσυνάρτηση που την περιγράφει να προστεθεί με την κυματοσυνάρτηση που βρήκαμε προηγουμένως, πριν κάνουμε την ύψωση στο τετράγωνο. Η κυματοσυνάρτηση των αδιατάρακτων σωματιδίων έχει την μορφή των θετικών Γκαουσιανών που δώσαμε αρχικά. Έτσι η κυματοσυνάρτηση μετά το χτύπημα θα συμβάλλει ενισχυτικά με την αδιατάρακτη μόνο στο τμήμα που βρίσκεται αρνητικά της τιμής p=0, ενώ θα συμβάλλει αποσβεστικά στο τμήμα που βρίσκεται θετικά της τιμής p=0. (Το αντίθετο βέβαια θα συμβεί αν τα σωματίδια είχαν ετερόσημα φορτία.). Έτσι μετά από λίγο χρόνο η τελική πια κυματοσυνάρτηση στο χώρο των ορμών θα μοιάζει με την παρακάτω εικόνα.  Υψώνοντας τώρα στο τετράγωνο την κυματοσυνάρτηση αυτή παίρνουμε την κατανομή πιθανότητας η οποία ξεκάθαρα μας λέει ότι η κορυφή της έχει μετακινηθεί προς τα’ αριστερά. Δηλαδή ότι το σωματίδιο που χτυπήθηκε από το εν δυνάμει φωτόνιο έχει απωθηθεί από το άλλο σωματίδιο! Στην παραπάνω μελέτη δεν λάβαμε υπ όψιν τις δυνατότητες ανταλλαγής μεγαλύτερου αριθμού φωτονίων, διότι τα πλάτη πιθανότητας γι’ αυτές είναι αρκετά μικρότερα, σύμφωνα με τους κανόνες της κβαντομηχανικής και μόνο για πολύ μεγαλύτερα χρονικά διαστήματα θα έπαιζαν ρόλο. Το σημαντικό συμπέρασμα από όλη αυτή την ανάλυση είναι ότι το φωτόνιο «δεν ξέρει» τι είδους σωματίδιο πρόκειται να χτυπήσει. Η διάκριση μεταξύ έλξης και άπωσης πραγματικά γίνεται όταν η κυματοσυνάρτηση μετά το χτύπημα συμβάλλει με την αδιατάρακτη κυματοσυνάρτηση. |
|||
|