Πυρηνικό σπιν και μαγνητική ροπή

Άρθρο, Δεκέμβριος 2002

Ένα αποτέλεσμα που προκάλεσε κατάπληξη και  μάλιστα συζητήθηκε στο συνέδριο του Solvay, ήταν η τιμή της πυρηνικής μαγνητικής ροπής του πυρήνα του υδρογόνου (πρωτονίου).

Μετά το φημισμένο πείραμα Stern-Gerlach με το οποίο έδειξαν ότι τα ηλεκτρόνια παρουσιάζουν μαγνητική ροπή λόγω σπιν, ο Stern με τους συνεργάτες του επανέλαβε το πείραμα του με μόρια υδρογόνου. Έτσι μέτρησε την πυρηνική μαγνητική ροπή του υδρογόνου, η οποία είναι μικρότερη του ηλεκτρονίου κατά τρεις τάξεις λόγω της μεγαλύτερης μάζας του πρωτονίου, όπως φαίνεται και από τον τύπο της μαγνητόνης του Bohr.

Μια πρώτη εκτίμηση της πυρηνικής μαγνητικής ροπής θα ήταν ότι αυτή είναι μικρότερη κατά το 1/1836 όσο και ο λόγος των μαζών ηλεκτρονίου-πρωτονίου. Μάλιστα ο Pauli είχε αναφέρει στον  Stern ότι είναι χαμένος χρόνος το πείραμα του γιατί είναι γνωστό το αποτέλεσμα. Στο τέλος όμως βρήκαν πειραματικά ότι ο λόγος αυτός ήταν διαφορετικός από τον θεωρητικά υπολογισμένο. Κι αυτό το αποτέλεσμα έδειξε ότι το πρωτόνιο έχει μια σύνθετη δομή (από κουάρκ).

Πυρηνικό σπιν και μαγνητική ροπή

Όπως τα ηλεκτρόνια έχουν μια εγγενή στροφορμή, το σπιν, έτσι και οι πυρήνες έχουν και αυτοί μια εγγενή στροφορμή, δηλαδή σπιν. Το μέτρο της εγγενούς πυρηνικής στροφορμής ισούται με:

Ο κβαντικός αριθμός Ι ονομάζεται πυρηνικό σπιν και μπορεί να είναι ακέραιος ή και ημιακέραιος. Η μέγιστη συνιστώσα της πυρηνικής στροφορμής σε οποιονδήποτε άξονα, μπορεί να είναι Ι·(h/2π ).

Στην πυρηνική στροφορμή αντιστοιχεί η μαγνητική ροπή του πυρήνα, σε αντιστοιχία με την μαγνητική ροπή λόγω σπιν του ηλεκτρονίου. Εδώ όμως η μαγνητική ροπή ενός πυρήνα εκφράζεται με πυρηνικές μαγνητόνες μn. Η μονάδα αυτή της πυρηνικής ροπής ορίζεται ως: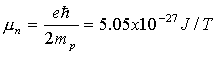

 

Ο ορισμός αυτός είναι αντίστοιχος της μαγνητόνης του Bohr μΒ με την οποία μετρείται η μαγνητική ροπή σπιν των ελεύθερων ηλεκτρονίων. Η τιμή της πυρηνικής μαγνητόνης είναι μικρότερη κατά 2.000 φορές από την μαγνητόνη του Bohr λόγω της διαφοράς μάζας του πρωτονίου από το ηλεκτρόνιο.

Το περίεργο όμως είναι ότι η μαγνητική ροπή του ελεύθερου πρωτονίου δεν ισούται με ένα μn όπως θα αναμέναμε, αλλά με 2.7928·μn.

Ενώ η μαγνητική ροπή του νετρονίου είναι -1.9135·μn. Το αρνητικό πρόσημο δηλώνει ότι η μαγνητική ροπή του νετρονίου έχει αντίθετη κατεύθυνση από την αντίστοιχη στροφορμή του.

Ο πυρήνας μέσα σε ένα εξωτερικό μαγνητικό πεδίο (Κλασσική προσέγγιση)

Σε αυτή την παράγραφο, θα πάρουμε μια "κλασσική" όψη της συμπεριφοράς του πυρήνα - δηλαδή τη συμπεριφορά ενός φορτισμένου σωματιδίου σε ένα μαγνητικό πεδίο.
Φανταστείτε έναν πυρήνα (με σπιν 1/2) σε ένα μαγνητικό πεδίο. Αυτός ο πυρήνας είναι στο χαμηλότερο επίπεδο ενέργειας και περιστρέφεται γύρω από τον άξονά του. Όταν όμως εφαρμοστεί ένα εξωτερικό μαγνητικό πεδίο, αυτός ο άξονας της περιστροφής μεταπίπτει (precess) γύρω από την διεύθυνση του Β, δηλαδή ο άξονας της μαγνητικής ροπής μ περιστρέφεται γύρω από το Β.  Η κυκλική συχνότητα της μετάπτωσης καλείται συχνότητα μετάπτωσης Larmor, ( ω_L ) , προς τιμήν του Άγγλου φυσικού  Larmor (1857-1942),  και είναι ανάλογη προς το εξωτερικό μαγνητικό πεδίο. 

Αυτό ακριβώς περιγράφεται σχηματικά στο παρακάτω σχήμα , όπου το μαγνητικό πεδίο έχει την κατεύθυνση του θετικού άξονα z. Αν το εξωτερικό μαγνητικό πεδίο είναι Β=1 Τ, τότε η συχνότητα Larmor ενός πρωτονίου στο πεδίο αυτό ισούται με 42.577 MHz.

Όταν ένας πυρήνας ο οποίος έχει μαγνητική ροπή βρεθεί σε εξωτερικό μαγνητικό πεδίο Β, η μαγνητική ροπή εκτελεί γωνιακή μετάπτωση γύρω από τον άξονα του μαγνητικού πεδίου, με συχνότητα η οποία είναι ανάλογη προς το πεδίο.

Η δυναμική ενέργεια του πυρήνα που κάνει μετάπτωση δίνεται από την σχέση:

E = - μ Β cosθ

όπου θ είναι η γωνία μεταξύ της κατεύθυνσης του εξωτερικού πεδίου και του άξονα της περιστροφής του πυρήνα

Όταν η προβολή της μαγνητικής ροπής μ κατά τη διεύθυνση του μαγνητικού πεδίου είναι μ, η δυναμική ενέργεια του δίπολου ισούται με -μ·Β (αυτή είναι και η ελάχιστη τιμή της). Όταν όμως η μ έχει αντίθετη κατεύθυνση από το μαγνητικό πεδίο, τότε η δυναμική ενέργεια του δίπολου ισούται με τη μέγιστη τιμή της, που είναι μ·Β. 

Εάν ο πυρήνας απορροφήσει ενέργεια, τότε η γωνία της μετάπτωσης, Θ , θα αλλάξει. Για έναν πυρήνα με σπιν 1/2, όπως θα δούμε και στην κβαντική αντιμετώπιση, ο προσανατολισμός της μαγνητικής ροπής μπορεί να είναι μόνο, είτε παράλληλος (ελάχιστη τιμή ενέργειας), είτε αντιπαράλληλος  με το μαγνητικό πεδίο (μέγιστη τιμή ενέργειας). Η απορρόφηση τότε ενέργειας μέσω κάποιας ακτινοβολίας, αναγκάζει τη μαγνητική ροπή έτσι ώστε αυτή να γίνει αντίθετη με το πεδίο (η υψηλότερη κατάσταση ενέργειας).

Αν χρησιμοποιήσουμε την τεχνική που λέγεται πυρηνικός μαγνητικός συντονισμός μπορούμε να ανιχνεύσουμε μεταβάσεις ανάμεσα σε αυτές τις δύο καταστάσεις σπιν. Εφαρμόζουμε πρώτα το σταθερό πεδίο Β για να προσανατολίσουμε τις μαγνητικές ροπές. Ταυτόχρονα εφαρμόζουμε και ένα ασθενές αλλά ταλαντούμενο μαγνητικό πεδίο, (μέσω κάποιας ακτινοβολίας), κάθετο στο πρώτο Β. Όταν η συχνότητα ταλάντωσης του ασθενούς  πεδίου γίνει ίση με τη συχνότητα μετάπτωσης Larmor, τότε η ροπή που δρα πάνω στις μεταπίπτουσες ροπές τις αναγκάζει να αλλάξουν κατάσταση και να μεταβούν από τη μια στην άλλη. Το καθαρό αποτέλεσμα των μεταβάσεων αυτών είναι απορρόφηση ενέργειας από τον πυρήνα, κάτι που ανιχνεύεται πειραματικά.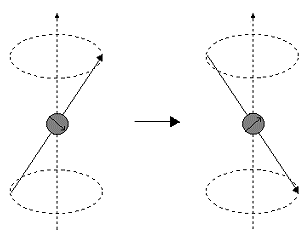

Αν χρησιμοποιήσουμε την τεχνική που λέγεται πυρηνικός μαγνητικός συντονισμός μπορούμε να ανιχνεύσουμε μεταβάσεις ανάμεσα σε αυτές τις δύο καταστάσεις σπιν. Εφαρμόζουμε πρώτα το σταθερό πεδίο Β για να προσανατολίσουμε τις μαγνητικές ροπές. Ταυτόχρονα εφαρμόζουμε και ένα ασθενές αλλά ταλαντούμενο μαγνητικό πεδίο, κάθετο στο πρώτο Β. Όταν η συχνότητα ταλάντωσης του ασθενούς  πεδίου γίνει ίση με τη συχνότητα μετάπτωσης Larmor, τότε η ροπή που δρα πάνω στις μεταπίπτουσες ροπές τις αναγκάζει να αλλάξουν κατάσταση και να μεταβούν από τη μια στην άλλη. Το καθαρό αποτέλεσμα των μεταβάσεων αυτών είναι απορρόφηση ενέργειας από τον πυρήνα, κάτι που ανιχνεύεται πειραματικά.

Πυρηνικό σπιν και διαχωρισμός των επιπέδων ενέργειας σε ένα μαγνητικό πεδίο (Κβαντική προσέγγιση)

Τα υποατομικά σωματίδια (ηλεκτρόνια, πρωτόνια και νετρόνια) μπορούν να τα φανταστούμε ότι περιστρέφονται γύρω από τους άξονές τους. Σε πολλά άτομα (όπως στον άνθρακα ¹² C) αυτά τα σπιν είναι σε ζεύξη, δηλαδή το ένα αντίθετο του άλλου, έτσι ώστε ο πυρήνας του ατόμου να μην παρουσιάζει κανένα συνολικό σπιν. Εντούτοις, σε μερικά άτομα (όπως στο ¹H και στον άνθρακα ¹³C) ο πυρήνας παρουσιάζει ένα συνολικό σπιν. Οι κανόνες για τον καθορισμό του καθαρού σπιν ενός πυρήνα είναι οι ακόλουθοι:

1. Εάν ο αριθμός νετρονίων και ο αριθμός πρωτονίων είναι και οι δύο άρτιοι, τότε ο πυρήνας δεν έχει ΚΑΝΕΝΑ σπιν.

2. Εάν ο αριθμός νετρονίων συν τον αριθμό πρωτονίων είναι περιττός, τότε ο πυρήνας έχει ένα σπιν ημιακέραιο (δηλ. 1/2, 3/2, 5/2)

3. Εάν ο αριθμός νετρονίων και ο αριθμός πρωτονίων είναι και οι δύο περιττοί, τότε ο πυρήνας έχει ένα ακέραιο σπιν (δηλ. 1, 2, 3)

Το συνολικό σπιν, Ι, είναι σημαντικό. Η κβαντομηχανική μας λέει ότι ένας πυρήνας με σπιν Ι θα έχει 2Ι+1 δυνατούς προσανατολισμούς του σπιν. Έτσι ένας πυρήνας με σπιν 1/2 θα έχει 2 δυνατούς προσανατολισμούς. Χωρίς εξωτερικό μαγνητικό πεδίο, αυτοί οι προσανατολισμοί είναι ίσης ενέργειας. Εάν όμως εφαρμοστεί ένα μαγνητικό πεδίο, τότε τα επίπεδα της ενέργειας διαχωρίζονται. Σε κάθε επίπεδο ενέργειας, αντιστοιχεί ένας μαγνητικός κβαντικός αριθμός του σπιν, m .

Το πρωτόνιο το οποίο έχει σπιν ½, μπορεί να καταλάβει μία από δύο πιθανές ενεργειακές καταστάσεις όταν βρεθεί σε εξωτερικό μαγνητικό πεδίο. Η χαμηλότερη, ενεργειακή κατάσταση, Ε1, από τις δύο αντιστοιχεί στην περίπτωση που το σπιν του πρωτονίου έχει την ίδια κατεύθυνση με το μαγνητικό πεδίο, ενώ η υψηλότερη, η Ε2 στην περίπτωση που το σπιν είναι αντιπαράλληλο με το πεδίο. Το αντίθετο συμβαίνει με τα ηλεκτρόνια διότι έχουν αρνητικό ηλεκτρικό φορτίο.

Όταν ο πυρήνας βρίσκεται σε ένα μαγνητικό πεδίο, οι αρχικοί πληθυσμοί των επιπέδων ενέργειας καθορίζονται από τη θερμοδυναμική ισορροπία, όπως περιγράφονται από την κατανομή Boltzmann. Αυτό είναι πολύ σημαντικό, και σημαίνει ότι το χαμηλότερο επίπεδο ενέργειας περιέχει ελαφρώς περισσότερους πυρήνες από ό,τι το υψηλότερο επίπεδο ενέργειας.

Είναι δυνατόν να διεγερθούν αυτοί οι πυρήνες σε υψηλότερο επίπεδο αν πέσει πάνω τους ηλεκτρομαγνητική ακτινοβολία. Η συχνότητα της ακτινοβολίας που απαιτείται καθορίζεται από τη διαφορά της ενέργειας μεταξύ των επιπέδων ενέργειας.

Υπολογισμός της ενέργειας μετάβασης

Ο πυρήνας έχει ένα θετικό φορτίο και περιστρέφεται. Αυτό παράγει ένα μικρό μαγνητικό πεδίο. Ο πυρήνας επομένως κατέχει μια μαγνητική ροπή, μ, που είναι ανάλογη με το σπιν του, Ι

Η σταθερά, γ , καλείται γυρομαγνητικός λόγος και είναι μια θεμελιώδης πυρηνική σταθερά η οποία έχει μια διαφορετική τιμή για κάθε πυρήνα. το h είναι η σταθερά του Planck.

Η ενέργεια κάθε επιπέδου ενέργειας δίνεται από

Όπου B είναι η ένταση του μαγνητικού πεδίου στον πυρήνα .

Για ένα πυρήνα με σπιν 1/2, η διαφορά στην ενέργεια μεταξύ των επιπέδων (η ενέργεια μετάβασης) μπορεί να βρεθεί από τη διαφορά:

Αυτό σημαίνει ότι εάν το μαγνητικό πεδίο, B , αυξάνεται, έτσι αυξάνεται και η ΔΕ. Επίσης σημαίνει ότι εάν ένας πυρήνας έχει ένα σχετικά μεγάλο γυρομαγνητικό λόγο, τότε η Διαφορά Ενέργειας ΔΕ είναι αντίστοιχα μεγάλη.

Είναι σημαντικό να αναγνωριστεί ότι μόνο ένα ποσοστό των πυρήνων "στόχων" βρίσκονται στην χαμηλότερη κατάσταση ενέργειας (και μπορεί να απορροφήσει την ακτινοβολία). Επίσης οι πυρήνες που θα βρεθούν στην υψηλότερη κατάσταση ενέργειας (διεγερμένοι), θα επιστρέψουν στην χαμηλότερη κατάσταση ενέργειας εκπέμποντας αντίστοιχη ακτινοβολία μ' αυτήν που απορρόφησαν για να βρεθούν εκεί. Έτσι υπάρχει η πιθανότητα πως από την αποδιέγερση και την σύγχρονη διέγερση άλλων πυρήνων, οι πληθυσμοί των υψηλότερων και χαμηλότερων επιπέδων ενέργειας μπορεί να γίνουν ίσοι. Εάν αυτό συμβεί, τότε δεν θα υπάρξει καμία περαιτέρω απορρόφηση της ακτινοβολίας. Λέμε τότε ότι το σύστημα των σπιν είναι κορεσμένο .